Функціонал оцінювання

Коли множина стратегій суб’єкта керування 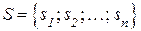та множина станів економічного середовища є дискретними, функціонал оцінювання задається матрицею:

,

елемент якої — це кількісна оцінка рішення (стратегії) s_kÎS за умови, що середовище перебуває у стані q _j Î Q.

При цьому кожному рішенню s_k відповідає вектор оцінювання

F_k = { f_{k 1}; f_{k 2}; …; f_kn }, k = 1,..., m.

Визначення функціонала оцінювання (платіжної матриці) у формі 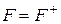(позитивний інгредієнт) використовують для оптимізації таких категорій, як виграш, корисність, ефективність, прибуток, надійність, імовірність удачі (ймовірність досягнення поставленої цілі) тощо. У формі (негативний інгредієнт) функціонал використовується для оптимізації таких категорій, як програш, затрати, збитки, ризик, імовірність невдачі тощо.

Матриця ризику

Матрицю ризику також називають матрицею невикористаних можливостей. Величини її елементів 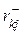вказують на збитки (невикористані можливості), які може отримати СПР у випадку вибору ним k -ої стратегії 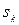в умовах j -го стану економічного середовища 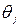, порівняно з результатом, який отримав би СПР при виборі найвигіднішої для нього стратегії в умовах цього ж стану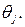

Елементи матриці ризику знаходять за однією з двох формул:

1) якщ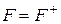о , то

,

2) якщо , то

.

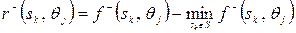Очевидно, що матриця ризику має негативний інгредієнт:

.

Поняття інформаційної ситуації

Під інформаційною ситуацією з погляду суб’єкта керування (залежно від ступеня його інформованості) розуміють певний ступінь градації невизначеності щодо перебування економічним середовищем в одному зі своїх можливих станів у момент прийняття рішення суб’єктом управління (гравцем).

Класифікатор інформаційних ситуацій, що характеризують поведінку економічного середовища при “виборі” свого стану в процесі прийняття рішення можна побудувати таким чином [1, 2, 3, 5].

Перша інформаційна ситуація – характеризується заданим розподілом апріорних ймовірностей станів економічного середовища 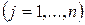, тобто вважаються відомими імовірності реалізації j- го стану: 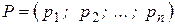, для яких повинні виконуватись такі умови: 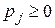, 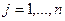(достатня за обсягом інформація).

Друга інформаційна ситуація – характеризується можливістю оцінити параметри (числові характеристики), які характеризують розподіл апріорних ймовірностей станів економічного середовища (математичне сподівання, дисперсію) хоча сам закон розподілу ймовірності є невідомим (достатня за обсягом інформація).

Третя інформаційна ситуація – характеризується певною системою (лінійних чи нелінійних) співвідношень пріоритету стосовно елементів множини Q – станів економічного середовища (обсяг інформації про економічне середовище недостатній).

Четверта інформаційна ситуація – характеризується, з одного боку, невідомим розподілом апріорних імовірностей станів економічного середовища, а з іншого боку – відсутністю активної протидії економічного середовища цілям суб'єкта управління.

П’ята інформаційна ситуація – характеризується абсолютно протилежними (антагоністичними) інтересами СПР та економічного середовища, тобто має місце конфлікт між ними. При цьому економічне середовище є активним[1] і являє собою зловмисного противника. (Це ситуація, коли обсяг інформації про поведінку економічного середовища достатній).

Шоста інформаційна ситуація – характеризується, як проміжна між першою та п’ятою інформаційними ситуаціями, коли одночасно з наявністю певної інформації щодо розподілу Р апріорних імовірностей , 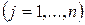економічне середовище не є пасивним.

Слід зауважити, що кожній інформаційній ситуації відповідає свій набір критеріїв прийняття рішень.

Прийняття рішень у полі першої інформаційної ситуації

Перша інформаційна ситуація є поширеною в більшості практичних задач прийняття рішень за умов ризику. При цьому ефективно використовуються методи теорії ймовірності та математичної статистики, особливо точкові статистичні оцінки.

Розглянемо деякі з основних критеріїв прийняття рішень у полі першої інформаційної ситуації.

1) Критерій Байєса. Згідно з критерієм Байєса оптимальне рішення 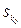(чи множина оптимальних рішень) у випадку, коли визначається умовою:

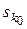:[2]⁾ В 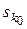⁺(; Р) = 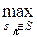В ⁺(s_k; Р).

Величина 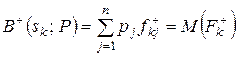називається байєсівською оцінкою рішення (стратегії)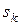 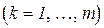і є математичним сподіванням випадкової величини, що задається вектором оцінювання .

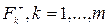Якщо функціонал оцінювання має негативний інгредієнт , тобто відображає ризики, збитки, непередбачені виплати тощо, то величину називають байєсівською оцінкою ризику рішення (стратегії) 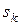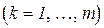. У цьому випадку оптимальне рішення (стратегія) визначається умовою:

.

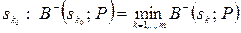Слід відмітити, що як показують дослідження, навіть у випадку сприятливої щодо СПР ситуації рішення, прийняте лише на основі критерію Байєса, неадекватне, тобто воно не враховує всі аспекти реальної ситуації (оскільки він не враховує варіацію). Тому оцінки, отримані згідно з цим критерієм, часто використовують як складові більш складних критеріїв, що враховують розкид значень функціоналу оцінювання на множині сценаріїв (це розглядатиметься далі).

2) Критерій мінімальної дисперсії. Незалежно від інгредієнта функціонала оцінювання оптимальне рішення (стратегія) 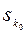може визначатись умовою:

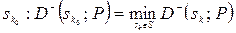
де 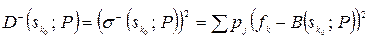- дисперсія випадкової величини, що задається вектором оцінювання .

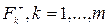3) Критерій мінімальної семіваріації. Незалежно від інгредієнта функціонала оцінювання оптимальне рішення (стратегія) 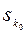може визначатись умовою:

: ,

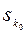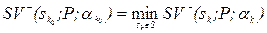де 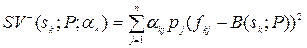– семіваріація випадкової величини, що задається вектором оцінювання 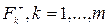, a _k = 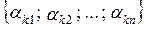– вектор індикаторів несприятливих відхилень для рішення s_k відносно байєсівської оцінки В (s_к; Р) цього рішення (k = 1, ..., m).

4) Критерій мінімального коефіцієнта варіації. Якщо функціонал оцінювання має позитивний інгредієнт 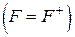, то оптимальним слід вважати рішення (стратегію)

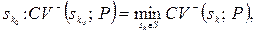
де 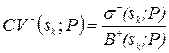– величина коефіцієнта варіації для рішення s_k.

5) Критерій мінімального коефіцієнта семіваріації. Якщо F = 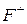, то оптимальним слід вважати рішення

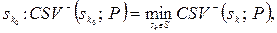
де 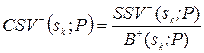– величина коефіцієнта семіваріації для рішення s_k.

Прийняття рішень у полі другої інформаційної ситуації

Зазначимо, що у цій ситуації висувається гіпотеза щодо класу функцій, якому належить цей (невідомий) розподіл, на основі статистичної інформації здійснюється перевірка цієї гіпотези і при наявності позитивного результату на основі ідентифікованого розподілу будується вектор 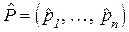, який розглядається як прийнятна оцінка розподілу ймовірності станів економічного середовища. Після цього, стосовно прийняття рішень, можна скористатись критеріями, що розглядались у випадку першої інформаційної ситуації.

Прийняття рішень у полі третьої інформаційної ситуації

Необхідно відмітити, що для цієї інформаційної ситуації характерним є те, що апріорі закон розподілу ймовірностей станів економічного середовища невідомий, але відомі деякі співвідношення пріоритету стосовно елементів множини станів економічного середовища. А тому суттєвою проблемою у цій ситуації є генерація гіпотез (допущень), на основі яких та наявної інформації здійснювалось би оцінювання розподілу ймовірностей станів економічного середовища.

Перша формула Фішберна. У випадку, коли на основі наявної (можливо й суб’єктивної) інформації можна побудувати ряд пріоритету щодо станів економічного середовища, тобто вважаючи, що 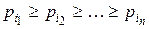Фішберн [7] висунув гіпотезу, що оцінки 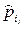апріорних ймовірностей 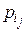можна будувати у вигляді спадної арифметичної прогресії. Він показав, що ці оцінки можна обчислювати за формулою:

.

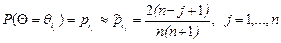Друга формула Фішберна. У випадку, коли апріорі можна стверджувати, що мають місце співвідношення пріоритету щодо станів економічного середовища

..........................................................

,

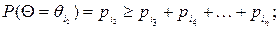
згідно з гіпотезою Фішберна [7] оцінки 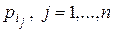, апріорних ймовірностей можна вибрати у вигляді спадної геометричної прогресії:

.

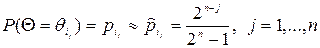Наступним етапом, після оцінювання розподілу ймовірності станів економічного середовища згідно з однією із формул Фішберна, є прийняття рішення з використанням критеріїв, розглянутих у випадку першої інформаційної ситуації.

Прийняття рішень у полі четвертої інформаційної ситуації

Для цієї інформаційної ситуації характерним є повне незнання закону розподілу ймовірностей станів економічного середовища. А тому вибір розподілу ймовірності станів економічного середовища, як і у двох попередніх випадках повинен базуватись на певних гіпотезах. У якості однієї з таких гіпотез можна використати принцип Бернуллі-Лапласа (принцип недостатніх підстав), згідно з яким можливі стани економічного середовища розглядаються як рівноімовірні випадкові події, якщо відсутня інформація про умови, за яких кожен стан може відбутися. Тобто вважати, що , .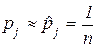

Прийняття рішень у полі п’ятої інформаційної ситуації

Ця інформаційна ситуація характеризується антагоністичними інтересами СПР та економічного середовища, тобто має місце конфлікт між ними. При цьому економічне середовище є активним, тобто таким, що активно протидіє досягненню найбільшої ефективності рішень, які приймаються СПР. Це досягається шляхом вибору таких своїх станів, які зводять до мінімуму ефективність процесу управління.

Необхідно зазначити, що основною стратегією для СПР у полі п’ятої інформаційної ситуації є забезпечення собі гарантованих рівнів значень функціоналу оцінювання.

1) Критерій Вальда. Коли F = F⁺, то згідно з критерієм Вальда оптимальне рішення вибирається за принципом maxmin (максиміну).

.

У випадку, коли 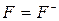, оптимальне рішення знаходиться згідно з принципом minmax (мінімаксу), а саме:

.

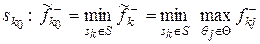Слід зазначити, що критерій Вальда надзвичайно консервативний, тобто безризиковий у такій ситуації, де недоцільно ризикувати.

2) Критерій домінуючого результату. Коли F = F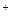, то згідно з критерієм домінуючого результату оптимальне рішення забезпечується maxmax (максимаксною) стратегією:

.

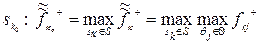У випадку, коли 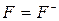оптимальне рішення забезпечується minmin (мінмінною) стратегією:

.

В основному цей критерій використовується як складова частина в процесі побудови складних моделей прийняття багатоцільових рішень для імітації найсприятливіших ситуацій (наприклад, в критерії Гурвіца, що використовується в полі шостої інформаційної ситуації).

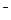3) Критерій мінімального ризику Севіджа. Цей критерій є одним з основних критеріїв, що відповідає принципу мінімаксу. Перш за все необхідно перейти від функціоналу оцінювання F до матриці ризику R. Тоді згідно з критерієм Севіджем оптимальним слід вважати рішення:

.

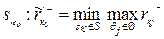Прийняття рішень у полі шостої інформаційної ситуації

Нагадаємо, що ця ситуація характеризується наявністю чинників, що зумовлюють «проміжну» між п’ятьма вищерозглянутими інформаційними ситуаціями поведінку економічного середовища щодо вибору своїх станів.

Класичними прикладами критеріїв прийняття компромісних рішень в полі шостої інформаційної ситуації критерій Гурвіца, модифіковані критерії та критерій Ходжеса-Лемана [1, 2, 3, 5, 6].

1) Критерій Гурвіца. Гурвіц запропонував використовувати зважену комбінацію найкращого та найгіршого. Такий підхід до вибору рішень відомий як критерій показника песимізму-оптимізму. Особливістю цього критерію є те, що в ньому передбачається не повний, а лише частковий антагонізм середовища та СПР.

Згідно з критерієм Гурвіца у випадку, коли F = F⁺, оптимальним є рішення

.

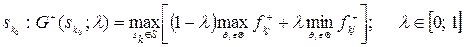Величину 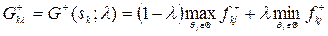називають l -показником Гурвіца для рішення s_k Î S.

У випадку, коли 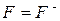, оптимальним є рішення

.

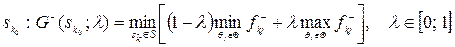Параметр l в обох випадках можна інтерпретувати як коефіцієнт несхильності до ризику.

2) Модифіковані критерії. Згідно з модифікованими критеріями у випадку, коли F = F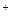, оптимальним є рішення

,

або ж у випадку, коли F = F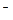, рішення

,

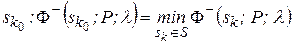де 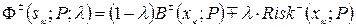; 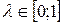, а в якості величини 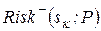можна використати середньоквадратичне , семіквадратичне 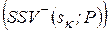відхилення тощо. Параметр 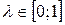, який використовується у зазначених вище критеріях, можна трактувати як коефіцієнт несхильності СПР до ризику.

3) Критерій Ходжеса-Лемана. Ходжес та Леман стоять на тій точці зору, що в практиці прийняття рішень в умовах невизначеності інформація про стан ЕС знаходиться між повним незнанням та точним знанням апріорного розподілу. Критерій Ходжеса-Лемана дає змогу використовувати всю інформацію, що її має суб’єкт управління, але в той же час забезпечує заданий рівень гарантії у випадку, коли ця інформація неточна. У деякому плані критерій Ходжеса-Лемана являє собою «суміш» кри­теріїв Байєса та Вальда.

Згідно з критерієм Ходжеса-Лемана у випадку, коли F = F⁺, оптимальним є рішення

.

Якщо ж , то оптимальним рішенням є

.

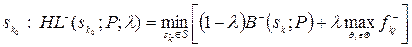Як і раніше, параметр lÎ[0,1], і його можна інтерпретувати як коефіцієнт несхильності до ризику.

Прийняття рішень, оптимальних за Парето

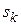
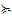
Необхідно відмітити, що згідно з Парето рішення s_k вважається не гіршим від рішення s_l (позначається: ), якщо для всіх елементів відповідних їм векторів мають місце оцінки 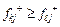якщо F = F 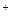чи , якщо F=F.

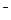Якщо хоча б для однієї компоненти 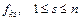вектора 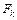має місце строга нерівність 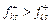(F = F⁺) чи 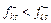(F = F 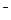), то рішення s_k вважається кращим за рішення s_l (записується ).

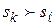Рішення 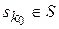є оптимальним за Парето, якщо в множині S не знайдеться рішення, краще від .

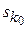Необхідно звернути увагу на те, що на практиці ситуація, коли рішення що приймається, буде оптимальним за Парето, є досить рідкісним явищем. А тому у разі відсутності рішення, оптимального за Парето, утворюють множину непокращуваних за Парето рішень . (Нагадаємо, що рішення називається покращуваним, якщо існує рішення 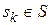таке, що 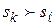). Тоді оптимальне рішення доцільно шукати серед елементів множини Парето S_П, використовуючи при цьому критерії, адекватні ситуації прийняття рішень.

Тема 4: Елементи теорії портфеля цінних паперів

1. Суть диверсифікації.

2. Суть управління портфелем цінних паперів.

3. Ризик портфеля цінних паперів.

4. Норма прибутку цінних паперів.

5. Ризик цінних паперів в абсолютному вираженні.

6. Кореляція цінних паперів та її застосування.

7. Портфель цінних паперів.

8. Задача збереження капіталу.

9. Задача одержання бажаного (фіксованого) прибутку.

Суть диверсифікації

Диверсифікація — це процес розподілу інвестованих засобів між різними об’єктами вкладення капіталу з метою зниження ступеня ризику, забезпечення більшої стійкості прибутків за будь-яких коливань дивідендів і ринкових цін на цінні папери (ЦП).

Загальним правилом інвестора щодо диверсифікації є таке: необхідно прагнути розподілити вкладення між такими видами активів, які показали за минулі роки, по-перше, різну щільність зв’язку (кореляцію) із загальноринковими цінами (індексами) і, по-друге, протилежну фазу коливання норми прибутку між собою (цін) всередині портфеля.

Ідею принципу диверсифікації та підхід до побудови оптимальних портфелів цінних паперів продемонструємо на прикладі побудови портфеля простих акцій.

Суть управління портфелем цінних паперів

Управління портфелем цінних паперів (ПЦП) — це планування, аналіз і регулювання структури портфеля, діяльність щодо його формування та підтримки з метою досягнення поставлених цілей при збереженні необхідного рівня його ризику та мінімізації затрат, пов’язаних з ним.

Основними цілями інвестування в ЦП у класичному аналізі є:

· одержання прибутку;

· збереження капіталу;

· забезпечення приросту капіталу (на базі зростання курсової вартості цінних паперів).

Досягнення цих цілей потребує дотримання певних умов. Так, наприклад, ціль «збереження капіталу» може бути реалізована тоді, коли портфель складають ліквідні ЦП.

Такі цілі можуть бути до певної міри альтернативними (суперечити одна одній) та відповідати різним типам ПЦП. Наприклад, якщо метою є одержання відсотка, то пріоритет віддається «агресивним» портфелям, які складаються з низьколіквідних та високори­зикованих ЦП молодих компаній, здатних, якщо цьому сприятимуть обставини, принести високі відсотки. І навпаки, якщо найважливішим для інвестора (менеджера) є збереження і приріст капіталу, то в портфель будуть залучені ЦП, що мають більшу ліквідність і які випущені відомими фірмами та державою, з невеликими ризиками й заздалегідь очікуваними сподіваними (середніми), хоча й невеликими відсотковими сплатами.

Ризик портфеля цінних паперів

Ризик ПЦП — це міра (ступінь) можливості того, що настануть обставини, за яких інвестор може понести збитки, спричинені інвестиціями в ПЦП, а також операціями, пов’язаними із залученням ресурсів до формування портфеля.

Портфельний ризик — агреговане поняття, яке, у свою чергу, включає багато видів конкретних ризиків: ліквідності, кредитний, капітальний, селекції тощо.

Найтиповішим управлінням портфелем є таке, кінцевою метою якого є прибутковість портфеля, тобто перевищення доходів від інвестицій в ЦП над затратами на залучення грошових ресурсів, необхідних для цих вкладень, за умови забезпечення певного ступеня ліквідності та ризику портфеля.

Норма прибутку цінних паперів

Основною характеристикою кожного ЦП є норма прибутку. Її обчислюють як відношення прибутку, що його приносить даний ЦП, до затрат, пов’язаних з купівлею цього ЦП. Якщо купівля ЦП здійснюється в період t ₀, то норма прибутку цього ЦП в період t обчислюється за формулою:

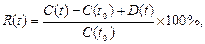
де C (t ₀) — ціна купівлі ЦП в період t ₀, C (t) — ціна (продажу) цього ЦП в t -ий період, D (t) — дивіденди, нараховані до t -го періоду.

Норма прибутку є одним з основних критеріїв, якими керуються інвестори під час прийняття рішення щодо купівлі цінного паперу.

Всі рішення, які торкаються інвестування в цінні папери, є такими, що стосуються майбутнього, але цілком очевидно, що будь-яке значення величини норми прибутку пов’язане з невизначеністю. Іншими словами, рішення, які стосуються інвестування в цінні папери, є рішеннями, що приймаються в умовах невизначеності і пов’язаного з цим ризику. Згідно з прийнятою раніше гіпотезою щодо норми прибутку (норма прибутку є випадковою величиною) це означає, що R (t) в кожний момент часу t може приймати різні значення з різними ймовірностями. Ці ймовірності залежать від ситуації на ринку ЦП, котра, в свою чергу, залежить від багатьох чинників, зокрема від загальної економічної ситуації.

Надалі будемо розглядати статичний ПЦП, тобто вважатимемо, що протягом періоду, який досліджується, норма прибутку певного ЦП може приймати різні значення (залежно від стану економічного середовища), але при цьому не має місця тенденція зміни значення цієї норми прибутку (залежно від часу). Такий підхід до побудови ПЦП є спрощеним, але він має широке використання.

На практиці при оцінці сподіваної норми прибутку часто виходять з припущення, що поводження ЦП у майбутньому великою мірою залежить від того, як формувались його норми прибутку у минулому. Це означає, що для статичної моделі ПЦП (або для близької до неї) майбутня норма прибутку може бути наближено визначена за допомогою норм прибутку, що мали місце у минулому.

Якщо позначити через Т кількість періодів, що минули (роки, місяці, тижні), то у випадку звичайної акції норма прибутку в t -му періоді визначається за формулою:

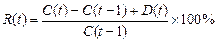, (4.1)

де C(t –1) — ціна ЦП в (t –1)-ий період, D (t) — дивіденди, нараховані в t -му періоді.

Сподівана норма прибутку цінних паперів

Введемо позначення:

Q = {q₁; q₂; …; q _n } — множина станів економічного середовища;

Р = { p ₁; p ₂; …; p_n } — розподіл ймовірностей станів економічного середовища;

R_i = { R_{i 1}; R_{i 2}; …; R_in } — множина значень норми прибутку і-го ЦП залежно від станів, що їх може приймати економічне середовище.

Величина

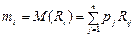(4.2)

має назву сподіваної норми прибутку і -го ЦП. Вона використовується в якості характеристики цього ЦП.

Приклад 1. Розглянемо дві акції виду А ₁ та А ₂. Для кожної з них можлива норма прибутку залежить від стану економіки. Експерти вказали на 5 можливих станів економіки, а також на ймовірність їх реалізації. Числові дані подано в табл. 4.1.

Таблиця 4.1

Стан економічного середовища	Ймовірність	Норма прибутку, % А 1 А2
Значне піднесення	0,1
Незначне піднесення	0,3
Стагнація	0,2
Незначна рецесія	0,3	– 2
Значна рецесія	0,1	– 10	– 5

Необхідно обчислити сподівану норму прибутку для цих ЦП.

Розв’язання. Сподівані норми прибутку позначимо відповідно через m ₁ та m ₂. Згідно з формулою (4.2) отримуємо, що m ₁ = 3,8%; m ₂ = 2,7%. Як бачимо, акція виду А ₁ характеризується вищою нормою прибутку, ніж акція виду А ₂, а тому, з точки зору максимізації прибутку, може бути обраною інвесторами акція виду А ₁.

Аналіз розв’язку. Невизначеність, пов’язана з величиною реалізованої норми прибутку, призводить до того, що інвестування в ЦП, а перш за все в звичайні акції, пов’язане з ризиком. Досить того, щоб настала стагнація або рецесія, тоді норма прибутку буде меншою, а прибуток перетвориться у збитки, причому ці збитки будуть більшими для акції виду А ₁. У зв’язку з цим слід зазначити, що акція виду А₁, приносячи більшу сподівану норму прибутку, обтяжена й більшим ризиком.

Якщо протягом Т періодів норма прибутку звичайної акції обчислюється згідно з формулою (1), то наближену оцінку сподіваної норми прибутку і-ої акції можна обчислити за формулою:

. (4.3)

Приклад 2. Розглянемо умовну акцію виду А, відносно якої маємо статистичну інформацію за останні 10 періодів (кварталів). Дані, а також обчислення норм прибутку, подано в табл. 4.2.

На базі цих даних, користуючись формулами (4.1) та (4.2), отримуємо значення сподіваної норми прибутку для акції виду А: m _A = 0,1 × 43,29» 4,33 (%). -

Таблиця 4.2

Період	Ціна акції, грн.	Дивіденд, грн.	Приріст ціни, грн.	Прибуток, грн.	Норма прибутку, %
t	C (t)	D (t)	C (t) – C (t –1)	C (t)– C (t –1) + D (t)	R(t)
					6,9
					12,67
		4,5	– 10	– 5,5	– 3,33
					6,45
		4,5	– 8	– 3,5	– 2,16
					7,14
		4,5		4,5	2,81
					11,25
			– 7	-3	– 1,71
		3,5		5,5	3,27
Сума	43,29

Ризик цінних паперів в абсолютному вираженні

Другою, поряд із сподіваною нормою прибутку, важливою характеристикою кожного цінного паперу є його ризик. Що стосується системи кількісних оцінок ризику, то деякі з найбільш простих і важливих оцінок були приведені раніше. Однією з них є варіація (дисперсія). У даному випадку можна говорити про варіацію (дисперсію) норми прибутку цінного паперу. Для і -го ЦП її можна обчислити за формулою:

(4.4)

Варіація (дисперсія) норми прибутку ЦП виражається у відсотках, піднесених до квадрата. Це, взагалі кажучи, дещо незручно з точки зору інтерпретації результатів. Цієї незручності позбавлена інша характеристика ступеня ризику — середньоквадратичне відхилення норми прибутку ЦП:

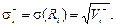
У випадку, коли є інформація про норму прибутку і -го ЦП у минулі Т періодів, варіацію можна обчислити за формулою:

.

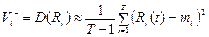Приклад 3. Виходячи з умови прикладу 1, обчислити ризик в абсолютному вираженні для кожного з ЦП виду А ₁ та А ₂ та порівняти їх між собою.

Розв’язання. Враховуючи, що m ₁ = 3,8%, m ₂ = 2,7%, згідно (4.4) отримуємо:

V₁ = 67,56; V₂ = 13,81;

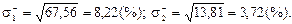
Як бачимо, ступінь ризику, пов’язаного з акцією виду А ₁, яка характеризується вищою сподіваною нормою прибутку, є значно вищим, ніж ризик, яким обтяжена акція виду А ₂.

Ризик цінних паперів у відносному вираженні

Розглянемо два цінних папери виду A ₁(m ₁; s₁) та A ₂(m ₂; s₂). Якщо для їх характеристик виконуються співвідношення m ₁ > m ₂ та s₁ < s₂, то в цьому випадку можна вважати, що ЦП виду A ₁ є кращим за ЦП виду A ₂ (символічно: A ₁ f A ₂).

Якщо ж m ₁ > m ₂ і при цьому s₁>s₂, то для порівняння ризику цих ЦП можна скористатись однією з відносних оцінок ризику:

· коефіцієнт варіації:

; (4.5)

· коефіцієнт семіваріації:

; (4.6)

· модифікований коефіцієнт варіації:

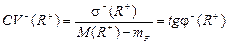; (4.7)

· модифікований коефіцієнт семіваріації:

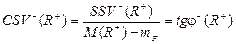, (4.8)

де m_F — норма прибутку безризикових або майже безризикових ЦП (наприклад, державних короткострокових облігацій, ЦП «старих фірм» тощо)

Приклад 4. Виходячи з умови прикладу 1, обчислити ризик у відносному вираженні для кожного із ЦП виду A ₁ та A ₂ і порівняти їх між собою.

Розв’язання. Оскільки згідно з умовою m ₁ = 3,8 > 2,7 = m ₂; s₁ = 8,22 > 3,72 = s₂, то для порівняння ЦП виду A ₁ та A ₂ скористаємось відносною оцінкою ризику, а саме — коефіцієнтом варіації:

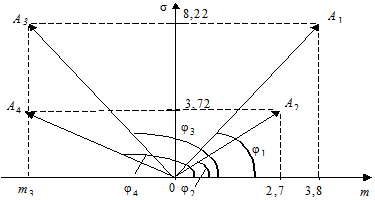
Рис. 4.1. Геометрична інтерпретація коефіцієнта варіації

На рис. 4.1 в системі координат «норма прибутку — ризик» акціям виду А ₁ відповідає точка А ₁ (m ₁;s₁), акціям виду А ₂ — точка А ₂ (m ₂; s₂), тобто їм відповідають радіуси-вектори 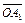та .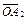

Враховуючи, що коефіцієнт варіації має негативний інгредієнт, приходимо до висновку, що з позиції цієї міри ризику перевага надається тим акціям, для яких відповідний радіус-вектор має менший кут нахилу до осі абсцис, тобто перевага надається ЦП виду А ₂.

Приклад 5. Виходячи з умови прикладу 1, а також враховуючи, що норма прибутку державних облігацій m_F = 3%, обчислити ризик кожного з цінних паперів виду А ₁ та А ₂ і порівняти їх між собою.

Розв’язання. Скористаємось модифікованим коефіцієнтом варіації (рис. 4.2):

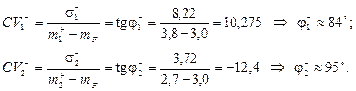
Враховуючи, що коефіцієнт варіації має негативний інгредієнт, перевагу слід надати акціям виду А₁.

Рис. 4.2. Геометрична інтерпретація модифікованого коефіцієнта варіації

Отриманий результат суперечить висновкам, зробленим у прикладі 3. Ця суперечність пояснюється тим, що модифікований коефіцієнт варіації за своєю суттю здійснює «фільтрацію» ЦП, відкидаючи ті акції, норма прибутку яких менша від фіксованої норми прибутку.

Зауваження 1. На рис. 4.1 наведено акції виду A ₃(m ₃; s₃) та A ₄(m ₄; s₄), для яких m ₃ = m ₄ < 0 та s₃ > s₄, але при цьому . У цій ситуації для порівняння акцій формально скористаємось відносною оцінкою ризику (коефіцієнтом варіації чи семіваріації). З урахуванням того, що , приходимо до висновку, що A ₃ f A ₄. Але здоровий глузд підказує, що має місце співвідношення A ₄ f A ₃.

Тому приходимо до висновку про недоцільність використання коєфіцієнта варіації (чи семіваріації) для порівняння ЦП у випадку, коли M (R⁺) < 0.

Слід також мати на увазі, що саме така ситуація виникла під час вивчення деяких ЦП Українських підприємств, виставлених на аукціон.

Аналогічна ситуація може виникнути і при використанні модифікованого коефіцієнта варіації (чи семіваріації). На рис. 4.2 порівняння ЦП виду A ₂ та A ₃ (які знаходяться в лівій півплощині по відношенню до прямої m = m_F) також приводить до протиріччя. А тому модифікований критерій слід використовувати лише для порівняння ЦП, що знаходяться праворуч по відношенню до прямої m = m_F (m = 3).

Кореляція цінних паперів та її застосування

Під час формування ПЦП істотну роль відіграє ще одна характеристика — кореляція ЦП. Вона характеризує взаємозв’язок між нормами прибутку двох цінних паперів. Міру щільності цього взаємозв’язку вимірюють за допомогою коефіцієнта кореляції.

Коефіцієнт кореляції є показником того, наскільки зв’язок між нормами прибутків акцій двох видів близький до строгої лінійної залежності. Він однаково ураховує і надто велику частку випадковості, і надто велику частку нелінійності цього зв’язку. Якщо розглядаються дві звичайні акції виду А ₁ та А ₂, то їхній коефіцієнт кореляції визначається за формулою:

де r₁₂ — коефіцієнт кореляції для акцій виду А ₁ та А ₂, cov(R ₁, R ₂) — коваріація випадкових величин R ₁ та R ₂. Очевидно, що cov(R_k, R_k) = 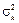, r _kk = 1, k = 1, 2.

Якщо коефіцієнт кореляції не дорівнює нулю, то він своєю величиною характеризує не тільки наявність, а й тісноту стохастичного зв’язку між R ₁ та R ₂.

Нагадаємо основні властивості коефіцієнта кореляції:

• коефіцієнт кореляції приймає значення в межах [– 1; 1];

• абсолютна величина коефіцієнта кореляції вказує на тісний взаємозв’язок норм прибутку акцій: чим більшою (ближчою до одиниці) є абсолютна величина, тим тісніше пов’язані між собою ці акції і чим меншою (ближчою до нуля) вона є, тим слабшим є зв’язок між цими акціями;

• знак коефіцієнта кореляції вказує напрямок взаємозв’язку норм прибутку акцій. Якщо він додатний, то маємо додатну кореляцію, коли зростання (зниження) норми прибутку однієї акції відбувається одночасно із зростанням (зниженням) норми прибутку другої акції. Коли ж коефіцієнт кореляції є від’ємною величиною, то маємо коефіцієнт так званої від’ємної кореляції акцій, коли зростання (зниження) норми прибутку однієї акції відбувається одночасно із зниженням (зростанням) норми прибутку другої.

Приклад 5. Розглянемо три різні акції виду А ₁, А ₂, А ₃. Дані стосовно їх норм прибутку та ймовірностей подано в табл. 4.3.

Необхідно обчислити відповідні коефіцієнти кореляції.

Таблиця 4.3

Стан економіки	Імовірність	Норма прибутку акцій, % А1 А2 А3
Значне піднесення	0,1
Незначне піднесення	0,3
Стагнація	0,3
Незначна рецесія	0,2
Значна рецесія	0,1	– 10

Розв’язання. Після відповідних обчислень одержимо такі значення сподіваних норм прибутку та середньоквадратичних відхилень акцій:

m ₁ = 5,5%, m ₂ = 13%, m ₃ = 8%; s₁ = 7,567%, s₂ = 8,718%, s₃ = 1,732%.

Знайдемо коваріацію між нормами прибутку для акцій А ₁ та А ₂:

cov(R ₁, R ₂) = 0,1 × (20 – 5,5)(30 – 13) + 0,3 × (10 – 5,5)(20 – 13) +
+ 0,3 × (5 – 5,5)(10 – 13) + 0,2 × (0 – 5,5)(5 – 13) + 0,1 × (– 10 – 5,5)(0 – 13) = 63,5.

Аналогічно знаходимо коваріації між нормами прибутку акцій виду А ₁ та А ₃, А ₂ та А ₃:

cov(R ₁, R ₃) = – 13; cov(R ₂, R ₃) = – 14.

Знайдемо тепер відповідні коефіцієнти кореляції:

r₁₂ = cov(R ₁, R ₂)/s₁s₂ = 63,5 / (7,567 × 8,718) = 0,963;

r₁₃ = cov(R ₁, R ₃)/s₁s₃ = – 13 / (7,567 × 1,732) = – 0,992;

r₂₃ = cov(R ₂, R ₃)/ s₂s₃ = – 14 / (8,718 × 1,732) = – 0,927.

На практиці додатна кореляція зустрічається значно частіше, ніж від’ємна. Це пов’язано з так званою силою прискорення ринку. Наприклад, дослідження, проведені на Нью-Йоркській біржі, показали, що переважна частина акцій має коефіцієнт кореляції в межах від 0,4 до 0,6.

Аналогічно тому, як це було зроблено при обчисленні сподіваної норми прибутку та ризику, оцінку коефіцієнта кореляції для двох видів акцій — вибірковий коефіцієнт кореляції — можна знайти на основі інформації про норми прибутку акцій у минулому.

Формула для обчислення вибіркового коефіцієнта кореляції двох видів акцій така:

,

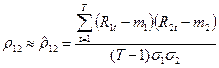де Т — кількість попередніх періодів, для яких маємо інформацію.

У зв’язку з випадковістю вибірки, вибірковий коефіцієнт кореляції може відрізнятися від нуля навіть тоді, коли між спостережуваними випадковими величинами відсутня кореляція.

Портфель цінних паперів

Узгодження максимізації норми прибутку і мінімізації ризику не є простим, оскільки на досить ефективному ринку цінні папери з високою нормою прибутку характеризуються відповідно високим ступенем ризику. Розсудливий інвестор шукає такі можливості щодо розміщення капіталу, при яких із збільшенням норми прибутку одночасно зменшувався б і ступінь ризику. Такі можливості дає йому формування портфеля цінних паперів. Сукупність придбаних цінних паперів становить портфель. Під структурою портфеля цінних паперів розуміють співвідношення часток інвестицій у цінні папери різних видів.

Математична модель ПЦП, сформованого з N цінних паперів, будується таким чином. Нехай R_k — норма прибутку k -го виду ЦП (k = 1, …, N), S_k — обсяг грошових активів, інвестованих в k- тий вид ЦП, S — обсяг всіх грошових активів, інвестованих в ПЦП. Покладемо

х_k = S_k / S, k = 1, …, N,

тобто х_k — це частка інвестицій у ЦП k -го виду. Очевидно, що x_k ³ 0 і при цьому

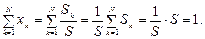
Структуру ПЦП відображає вектор X = { x ₁; ...; x_N }.

Тоді норма прибутку ПЦП, складеного з N видів ЦП

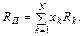
Cподівана норма прибутку цього ПЦП

тобто

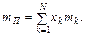
Ризик ПЦП згідно з класичним підходом обчислюється на основі дисперсії його норми прибутку:

V_П = D (R_П) = s²(R_П) = = M (R_П – m_П)².

Легко показати [3], що

,

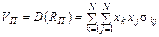де .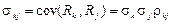

Однорідний портфель цінних паперів

Особливим випадком портфеля є однорідний портфель, тобто такий, який містить лише один вид цінних паперів.

Тоді для цього ПЦП

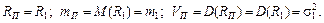
Портфель з двох видів цінних паперів

Нехай х ₁ та х ₂ частки інвестицій у ЦП виду А ₁ та А ₂, що складають портфель. Тоді, враховуючи що N = 2, отримуємо:

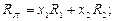
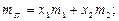
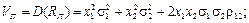
З урахуванням того, що х ₂ = 1 – х ₁, отримуємо:

(4.5)

тобто цільова функція V_П є функцією однієї змінної х ₁, а саме — параболою 2-го порядку. Оскільки х ₁ Î [0; 1], то для всіх значень параметрів s₁, s₂ і r₁₂ ця парабола проходить через точки А ₁(1; ) та А ₂(0; 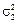), які відповідають однорідним ПЦП, складеним, відповідно, з ЦП виду А ₁ та виду А ₂.

Оскільки коефіцієнт кореляції r₁₂ приймає значення з проміжку [– 1; 1], то величина 1 – r₁₂ ³ 0. А тому коефіцієнт при 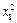для функції V_П

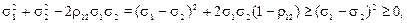
тобто парабола (4.5) є опуклою вниз і досягає свого мінімального значення у вершині 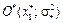. Функція V_П згідно зі своєю побудовою може набувати лише невід’ємних значень, а тому приходимо до висновку, що в системі координат (х ₁; V_П) вся парабола (4.5) лежить над віссю абсцис (рис. 4.3).

Надалі для визначеності щодо акцій виду A₁ та A₂ будемо вважати, що мають місце співвідношення:

М (R ₁) = m ₁ > m ₂ = М (R ₂);
s(R ₁) = s₁ > s₂ = s(R ₂).

Координати вершини параболи 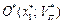обчислюються за формулами [4]:

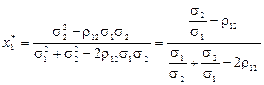; (4.6)

(4.7)

Згідно з системою рівнянь

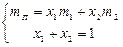
отримуємо, що

.

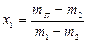Тоді

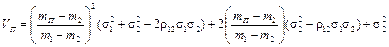. (4.8)

Отже, зв’язок між ризиком ПЦП V_П та його сподіваною нормою прибутку m_П також описується параболою другого порядку, і при цьому коефіцієнт при (m_П)² також набуває невід’ємного значення.

Легко переконатись, що графік функції (4.8) проходить через точки А ₁(m ₁; ) та А ₂(m ₂; 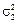) (рис. 4.4).

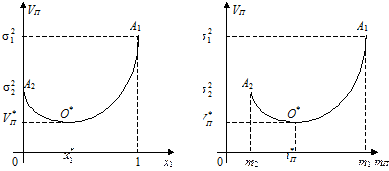
Рис. 4.3. Залежність ризику ПЦП від х 1 (частки акції першого виду в ПЦП)

Рис. 4.4. Залежність ризику ПЦП від mП (сподіваної норми прибутку ПЦП)

Парабола (4.8) має вершину 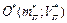, де

,

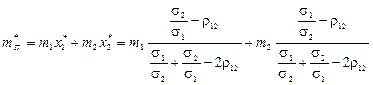а значення 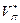обчислюється згідно з (4.7).

Сутність ефекту від диверсифікації при побудові ПЦП полягає в тому,що збільшення сподіваної норми прибутку m_П (починаючи з мінімально можливого допустимого значення) може привести (на певному етапі) до зменшення ризику V_П цього портфеля.

Згідно з рис. 4.4. при збільшенні m_П від значення m ₂ до m_П^* величина ризику ПЦП зменшується від 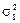до 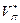= (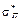)². Подальше збільшення m_П (від 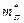до m ₁) призводить до збільшення величини ризику портфеля (від (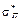)² до 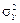). Отже, диверсифікація буде ефективною лише в тому разі, коли абсциса 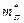вершини О^* параболи (4.8) буде належати проміжку [ m ₂; m ₁] і, відповідно, абсциса 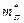вершини О^* параболи (4.5) — проміжку (0; 1).

Оскільки 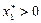, то з (4.6) випливає, що , тобто що r₁₂ Î [– 1; s₂/s₁). А тому можна зробити наступний висновок: для ПЦП, складеного з двох видів ЦП, диверсифікація дає ефективний результат щодо зменшення величини ризику лише в тому разі, коли коефіцієнт кореляції для норм прибутку цих ЦП r₁₂ Î [–1; r¢), де r¢ = .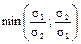

Приклад 6. Сподівана норма прибутку акцій виду А ₁ становить 60%, ризик цих акцій (середньоквадратчне відхилення) — 20%. Для акцій виду А ₂ відповідно сподівана норма прибутку — 40%, ризик — 15%. Коефіцієнт кореляції для цих акцій r₁₂ = 0,35. На основі цих акцій створюється ПЦП. Необхідно:

1) обчислити сподівану норму прибутку та ризик ПЦП, якщо акції виду А₁ складають 20% вартості цього портфеля;

2) обчислити сподівану норму прибутку та ризик ПЦП, якщо акції виду А₁ складають 80% вартості ПЦП;

3) створити оптимальний ПЦП (тобто такий, що має мінімальний ризик).

Розв’язання. 1) Згідно з умовою частка акцій виду А ₁ в ПЦП х ₁ = 0,20, а тому частка акцій виду А ₂ х ₂ = 0,80. Тоді

2) Оскільки в цьому випадку х ₁= 0,80, х ₂ = 0,20, то отримуємо:

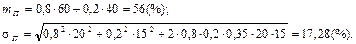
3) Оскільки 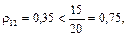то

-

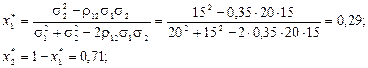
Приклад 7. Виходячи з умови прикладу 6, знайти структуру ПЦП:

а) сподівана норма прибутку якого становила б 50%; б) ризик якого становив би 16%.

Розв’язання.

а) Скориставшись тим, що

,

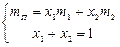отримуємо систему рівнянь:

.

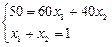Розв’язавши цю систему рівнянь, отримуємо, що x ₁ = 0,5, x ₂ = 0,5,

.

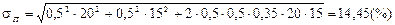б) Скориставшись тим, що

,

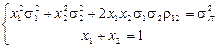отримуємо систему рівнянь

.

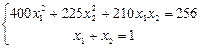Ця система рівнянь зводиться до квадратного рівняння:

415 x ₁² – 240 x ₁ – 31 = 0,

яке має корені x ¢ = – 0,109 та x ¢¢ = 0,687. Оскільки x ¢ < 0, то в ПЦП частка ЦП виду A ₁ становить x ₁ = x ¢¢ = 0,687, виду A ₂ — x ₂ = 1 –– x ¢¢ = 0,313.

Сподівана норма прибутку отриманого ПЦП становить

m_П = x ₁ m ₁ + x ₂ m ₂ = 0,69 × 60 = 0,31 × 40 = 53,84(%).

Портфель з багатьох видів цінних паперів

Перейдемо тепер до загального випадку, коли до складу ПЦП залучено N (N > 2) різних акцій.

Розглянемо, наприклад, три акції, що мають норми прибутку відповідно 15%, 10%, 5%, середньоквадратичні відхилення 10%, 7%, 3% і коефіцієнти кореляції r₂₃ = – 0,2; r₁₂ = – 0,4; r₁₃ = + 0,6. У системі координат m_П – s _П (норма прибутку — ризик, рис.5) побудуємо точки А ₁, А ₂, А ₃, що відповідають однорідним ПЦП, сформованим з відповідних акцій. На цьому ж рисунку побудуємо лінії (дуги), що відповідають ПЦП, сформованому з двох видів акцій (ÈА₃А₁; ÈА₃А₂; ÈА₂А₁).

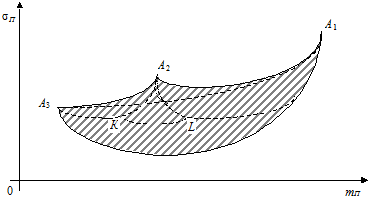
Рис. 4.5. Множина допустимих портфелів цінних паперів

Точкам К Î È А ₃ А ₂ та L Î È А ₂ А ₁ відповідають певні ПЦП, cформовані з двох (відповідно А ₃, А ₂ та А ₂, А ₁) видів акцій. Для цих портфелів можна розрахувати норми прибутку і ризики. Вважатимемо тепер, що кожний з цих портфелів є певного виду «цінним папером» відповідно К та L. А тому, в свою чергу, можна сформувати новий ПЦП для ЦП К та L. Такі ПЦП вже будуть включати по три акції (А ₁, А ₂, А ₃) і їм відповідає дуга È КL.

Міркуючи таким чином, приходимо до висновку, що кожна точка, яка належить до заштрихованої області (рис. 4.5), відповідає деякому ПЦП, сформованому з трьох видів акцій.

Допустимою множиною ПЦП називається область, точки якої характеризують ступінь ризику та норму прибутку портфеля за всіх можливих часток окремих акцій в портфелі (на рис. 4.5 — це область, обмежена жирною лінією).

Особливістю дуги È О*А ₁, яка належить допустимій множині, є те, що для будь-якої точки цієї дуги не можна вказати іншої точки допустимої області, для якої ПЦП був би кращим.

Ефективною множиною ПЦП називаються ті портфелі, що відповідають точкам дуги È О*А ₁. Тобто ефективним портфелем вважається такий, для якого в допустимій множині ПЦП не можна вказати іншого портфеля:

· з тим же значенням величини сподіваної норми прибутку і меншим ступенем ризику;

· з тим же значенням величини ризику і більшим значенням сподіваної норми прибутку.

Очевидно, що для ПЦП, складених з двох акцій, допустима множина збігається з множиною ефективних портфелів, і вони складають дугу È О*А ₁ (рис. 4.4).

Розглянемо тепер загальний випадок побудови ПЦП, сформованого з N ЦП. Як і раніше, позначимо через R_k, m_k = M (R_k), s _k — відповідно норму прибутку, спо

Дата добавления: 2014-01-11