Волновая функция заряженной частицы

Поскольку функция характеризует вероятность, то математический аппарат квантовой механики резко отличается от математического аппарата классической физики.

Предположим, что нам известна -функция какой либо частицы. Как теперь найти параметры этой частицы? Координаты 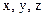. Импульс .

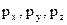Эта задача в квантовой механике решается своеобразным приемом. Каждой величине ставится в соответствие свой оператор. Подействовав этим оператором на -функцию находят искомый параметр.

Например.

Пусть частица двигается вдоль оси и пусть ее импульс определен точно. В этом случае, как мы уже видели, частице сопоставляется монохроматическая, плоская волна. Фаза этой монохроматической волны имеет вид:

Используя соотношения и 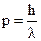, выражение для фазы волны перепишем в виде:

Волновая функция незаряженной частицы есть гармоническая функция sin или cos от 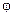. Если частица заряжена, то волновая функция комплексна:

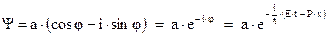(6)

Дата добавления: 2014-01-11