Элементы зонной теории твердых тел

(Энергетические уровни электронов в атоме. Возникновение энергетических зон при образовании твердого тела из изолированных атомов. Заполнение зон при абсолютном нуле. Металлы, диэлектрики и полупроводники по зонной теории. Собственная и примесная проводимости полупроводников. P-n-переход и его свойства.)

Природа носителей тока в металлах

Для выяснения ответа на этот вопрос был поставлен целый ряд опытов.

Опыт Рике (1901г). Он брал цилиндры различных металлов, с тщательно отшлифованными торцами, прижимал их друг к другу и пропускал через них ток в течение года (см. рис. 4.1). Затем эти цилиндры были разобраны и проанализированы на взаимное проникновение металлов. При этом оказалось, что результаты не превышают обычных, т.е. без пропускания тока.

Таким образом, ток в металлах не связан с переносом самого вещества металлов. Носители тока ‑ заряженные частицы, не связаны с атомами металла и одинаковы для всех металлов.

Далее, поскольку ток в металлах появляется даже при незначительной разности потенциалов, то эти носители довольно свободно перемещаются в металлах. Поэтому должны проявляться инерционные эффекты. Суть их заключается в том, что если образец металла двигать с ускорением (положительным или отрицательным), то носители заряда, вследствие существования явления механической инерции, будут не успевать за движением металла. Поэтому будет происходить скопление заряда у передней или задней стенки образца (см. рис. 4.2). Это неравномерное распределение заряженных частиц вызовет отличное от нуля электрическое поле. Следовательно, вольтметр, подключенный к передней и задней стенке металла, покажет разность потенциалов.

Знак разности потенциалов будет зависеть от знака носителей заряда. А величина разности потенциалов будет определяться как величиной заряда, так и их массой.

Такие опыты были проделаны в 1913 г Л.И.Мандельштамом и Н.Д Папалекси и в 1916 г Стюартом и Толменом.

В результате было установлено, что знак носителей заряда отрицательный и масса совпадает с массой электрона.

Таким образом, было окончательно установлено, что носителями тока в металлах являются свободные электроны.

Элементарная классическая теория металлов

Между атомами, расположенными в узлах кристаллической решетки металлов, существует сильное взаимодействие. Это приводит к тому, что самые внешние электроны переходят от одного атома к другому и т.д. Т.е. внешние электроны перестают принадлежать отдельным атомам, а становятся коллективной собственностью куска металла.

Это обстоятельство позволяет рассматривать металл, как кристаллическую решетку, в узлах которой находятся положительно заряженные ионы, а между ионами существует электронный газ.

Концентрация электронного газа для одновалентных ионов имеет величину, порядка

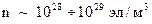
Взаимодействие электронов между собой и ионами решетки весьма велико, однако, среднюю силу, действующую на каждый электрон, можно считать равной нулю.

Взаимодействие электронов с решеткой и друг с другом можно рассматривать как ряд последовательных соударений и считать, что электрон обладает лишь кинетической энергией.

Т.е. электронный газ можно рассматривать как идеальный газ и применить к нему теорию идеального газа, или (как говорят) применить к нему статистику Максвелла-Больцмана (см. (I.2.45 ‑ I.2.46)).

Оценим скорость хаотического, теплового движения электронов в металле.

Электроны, обмениваясь при столкновениях энергией с ионами, будут обладать такой же температурой, как и металл. Поскольку по предположению они обладают только кинетической энергией, то можно записать:

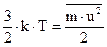
где, напомним, 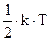‑ тепловая энергия приходящаяся на одну степень свободы, 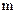‑ масса электрона. Отсюда

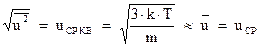
При комнатной температуре 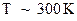средняя скорость электронов имеет величину, порядка

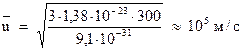
Если внутри металла создать однородное электрическое поле, то электроны приобретут дополнительную скорость 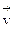, направленную против поля (т.к. заряд электрона отрицательный). Суммарная скорость электрона 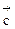равна векторной сумме:

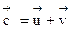
Отсюда

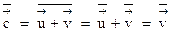
Т.е. средняя скорость электрона равна средней скорости упорядоченного движения. Оценим теперь величину этой средней скорости.

Для этого используем формулу (2.4) ‑ 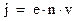. По техническим нормам, плотность тока в металлах, в частности меди, не должна превышать величины 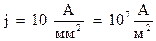. Следовательно, средняя скорость упорядоченного движения будет равна

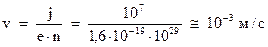
Т.е. ‑ . Таким образом, наличие электрического тока практически не увеличивает энергию электронов и, соответственно, не изменяет время между столкновениями

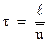
где 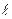‑ расстояние между узлами кристаллической решетки металла.

Закон Ома

Рассмотрим металлический проводник, подключенный к источнику тока. В этом случае внутри проводника, как мы видели, устанавливается однородное электрическое поле, напряженностью 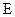. Электроны движутся в металле, соударяясь с ионами кристаллической решетки. Непосредственно после соударения с ионом направление и величина их скорости меняются случайным образом. Следовательно, непосредственно после соударения скорость электрона можно считать равной нулю.

После соударения на него действует сила со стороны электрического поля ‑ 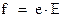. Под действием этой силы электрон приобретает ускорение

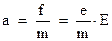
В результате, до следующего соударения его скорость возрастет до максимально возможной:

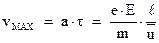
Затем, после соударения, скорость электрона снова станет равной нулю т т.д. (см. рис. 4.3). Средняя скорость такого направленного движения под действием электрического поля, будет равна:

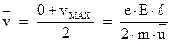
Поэтому, выражение для плотности тока будет иметь вид:

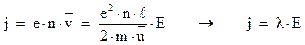
Таким образом, мы получили закон Ома в дифференциальной форме, где электропроводность металла 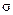определяется выражением:

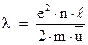(4.1)

Из этого выражения видно, что электропроводность зависит от свойств конкретного металла: 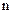‑ концентрации электронного газа, 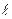‑ расстояние между узлами кристаллической решетки, 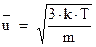‑ температуры металла.

Закон Джоуля-Ленца

Электроны, ускоряясь полем, получают дополнительную энергию, которую затем отдают ионам решетки при соударениях.

Хотя энергия, передаваемая в каждом отдельном случае, мала (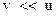), но она передается ионам непрерывно. Число соударений 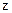, совершаемых за единицу времени, очень велико

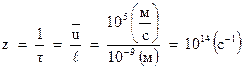
Поэтому и энергия, передаваемая за единицу времени ионной решетке будет значительна. Подсчитаем это количество энергии.

Средняя кинетическая энергия электрона в начале свободного пробега равна ‑ 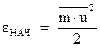, в конце ‑ 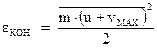. Приращение энергии будет равно:

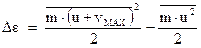
Сделаем преобразования:

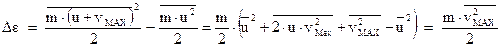
Это ‑ порция энергии, которая передается ионам при столкновении одного электрона. Чтобы получить энергию, выделяемую в единицу времени, данное выражение нужно умножить на число столкновений 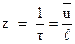. Чтобы получить выражение для энергии, выделяемой в единицу времени и в единице объема 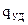, данное выражение надо умножить еще на 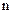. В итоге получим:

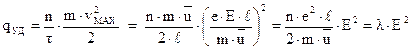
Здесь мы использовали выражение для электропроводности 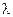, полученное выше.

Таким образом, мы пришли к дифференциальному закону Джоуля-Ленца.

Закон Видемана-Франца

Итак, электрический ток в металлах обусловлен наличием электронного газа. Но металлы отличаются от диэлектриков не только электропроводностью, но и значительной теплопроводностью. Следовательно, можно предположить, что высокая теплопроводность металлов по сравнению с диэлектриками обусловлена наличием электронного газа. Ведь с точки зрения классической теории металлы и диэлектрики ничем больше не отличаются.

Величину теплопроводности электронного газа можно оценить методами кинетической теории идеального газа. Из этой теории, в частности вытекает, что коэффициент теплопроводности определяется выражением (см. вывод формулы (I.2.51)):

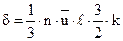
Найдем отношение коэффициента теплопроводности к коэффициенту электропроводности

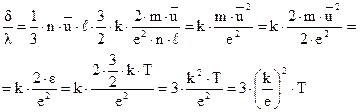
Это и есть закон Видемана-Франца, который экспериментально был установлен еще в 1853 году.

Отношение коэффициента теплопроводности к коэффициенту электропроводности для всех металлов должно быть одинаково и должно расти прямо пропорционально абсолютной температуре.

Трудности классической теории

Однако численный коэффициент в экспериментальном законе Видемана-Франца не совсем совпадал с теоретическим значением. Более того, когда Лоренц произвел более точный расчет, учитывая закон Максвелла о распределении электронов по скоростям, закон Видемана-Франца стал иметь вид:

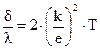(4.2)

Но при этом получилось еще большее расхождение с экспериментом.

Второе затруднение классической теории состоит в следующем.

Теплоемкость любого твердого тела, согласно экспериментальному закону Дюлонга-Пти, постоянна и равна 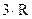, что и подтверждается опытами для всех твердых тел ‑ и проводников и диэлектриков.

Однако, согласно классическим воззрениям, в проводниках есть электронный газ, который также обладает теплоемкостью, равной ‑ 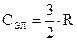. Отсюда вытекает, что теплоемкость проводника должна быть:

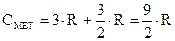
что, как мы видим, отличается от экспериментального закона Дюлонга-Пти.

Третье затруднение классической теории состоит в следующем.

Согласно классической теории:

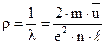
Подставляя сюда выражение для скорости хаотического теплового движения электронов, получим:

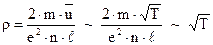
Таким образом, теория дает температурную зависимость удельного сопротивления в виде 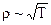, а на практике ‑ .

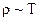И эти противоречия ни как не разрешимы в рамках классической теории

Лекция 16. (2 часа)

Дата добавления: 2014-01-11