Свойства бинарных отношений. 1. Рефлексивность. Отношение R называется рефлексивным, если (х, х)ÎR для любого хÎA

1. Рефлексивность. Отношение R называется рефлексивным, если (х, х)ÎR для любого хÎA. Примеры рефлексивных отношений: отношения "³", "£" на множестве R.

2. Антирефлексивность. Отношение R называется антирефлексивным, если (х, х)ÏR для любого хÎA. Примеры антирефлексивных отношений: отношения "<", ">" на множестве R.

Если R – антирефлексивное отношение, то xÏG_R(x) и хÏH_R(x) для любого хÎA.

3. Симметричность. Отношение R называется симметричным, если для любых x, yÎA из того, что (x, y)ÎR следует (y, x)ÎR и обратно. Примеры симметричных отношений: отношения "=" и "¹".

Если отношение R симметрично, то для любого хÎA

а) G_R(x) = H_R(x); б) R = R^–1.

4. Антисимметричность. Отношение R называется антисимметричным, если для любых x и y из A из одновременного выполнения условий (x, y)ÎR и (y, x)ÎR следует, что x = y. Пример антисимметричного отношения. Пусть А – множество людей в данной очереди. Отношение R – "не стоять за кем-то в очереди" будет антисимметричным.

Пусть х = ВАСЯ, а y = ИВАНОВ. Тот факт, что (x, y)ÎR означает, что "ВАСЯ не стоит в очереди за ИВАНОВЫМ", (y, x)ÎR – "ИВАНОВ не стоит за ВАСЕЙ". Очевидно, что одновременное выполнение обоих включений может быть, только если ВАСЯ и есть ИВАНОВ, т.е. x = y.

Отношение "³" также антисимметрично: если x ³ y и y ³ x, то x = y.

5. Асимметричность. Отношение R асимметрично, если R Ç R^-1= Æ, т.е. пересечение отношения R с обратным отношением пусто.

Эквивалентное определение асимметричности: из двух отношений (x, y) Î R и (y, x)ÎR одно не выполняется.

Примеры асимметричных отношений: ">", "<", "быть начальником".

Если R – асимметричное отношение, то из xRy следует y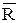x.

Для любого отношения R вводятся понятия симметричной части отношения R^s = R ÇR^–1 и асимметричной части отношения R^a = R \ R^s. Если отношение R симметрично, то R= R^s, если отношение R асимметрично, то R = R^a.

Примеры. Если R – "³", то R^–1 – "<", R^s – "=", R^a – ">".

6. Транзитивность. Отношение R транзитивно, если для любых x, y, zÎA из того, что (x, y)ÎR и (y, z)ÎR следует (x, z)ÎR.

Свойства транзитивного отношения:

а) RoR Í R;

б) для любого хÎA из yÎG_R(x) следует, что G_R(y) Í G_R(x).

Не транзитивным является отношение "¹". Пусть x = 2, y = 3, z = 2, тогда справедливо x ¹ y и y ¹ z, но x = z, т.е. (x, z)ÏR.

Отношение R₁ называется транзитивным относительно отношения R₂, если:

а) из (x, y)Î R₁ и (y, x)Î R₂ следует, что (x, z)Î R₁;

б) из (x, y)Î R₂ и (y, x)Î R₁ следует, что (x, z)Î R₁.

7. Негатранзитивность. Отношение R называется негатранзитивным, если`R транзитивно.

Примеры. Отношения R₁ –">" и R₂ –" ¹" негатранзитивны, так как отношения`R<sub>1</sub> – "£",`R₂ – "=" транзитивны. Возможно одновременное выполнение свойств транзитивности и негатранзитивности. Например, отношение R₁ одновременно транзитивно и негатранзитивно, а R₂ , как известно, транзитивным не является.

8. Полнота. Отношение R полно, если для любых x, yÎА либо (x, y)ÎR, либо (y, x)ÎR, либо оба отношения выполняются одновременно.

Свойства полных отношений:

а) G_R(x) È H_R(x) = А для любого хÎA;

б) полное отношение рефлексивно.

9. Слабая полнота. Отношение R называется слабо полным, если для любых х ¹ y из А или (x, y)ÎR, или (y, x)ÎR.

Пример слабо полного отношения. Пусть А – множество предприятий, "неблагополучных" в смысле своего бюджета. Отношение R "быть должным" является слабо полным, так как каждое из этих предприятий или кому-либо должно, или ему кто-то должен, но быть должным самому себе нельзя и (x, x)ÏR.

10. Ацикличность. Бинарное отношение R ациклично, если Rⁿ ÇR^–1= Æ для любого nÎ N. Иными словами, если из любой конечной цепочки отношений х₁Rx₂, x₂Rx₃,..., x_n-1Rx_n следует, что x₁ ¹ х_n, то отношение R ациклично.

Дата добавления: 2014-01-11