Лекция № ) Канал подвижной связи

Медленные замирания 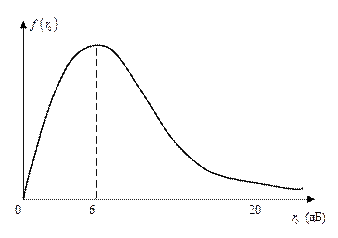. Интервал корреляции намного больше длительности элементарного символа (бита) .

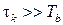Причины медленных замираний: изменение свойств среды распространения радиоволн в зависимости от метеорологических условий, времени суток, года, солнечной активности.

Закон распределения – логнормальный

где 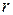- мгновенное значение огибающей сигнала, 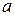- среднее значение огибающей, - дисперсия глубины замираний. В городских условиях = 10 дБ, в пригороде =6 дБ. При скорости МС 60 км/ч на несущей частоте 900 МГц длительность медленных замираний составляет 1…2 с.

Быстрые замирания. Интервал корреляции намного меньше длительности элементарного символа (бита) 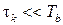. Причина быстрых замираний: многолучевое распространение – в основном за счет наличия городской застройки (закон Рэлея-Райса):

,

где - отношение мощности прямого (нефлуктуирующего) сигнала к средней мощности флуктуаций, - дисперсия глубины замираний, - модифицированная функция Бесселя 1-го рода нулевого порядка. Если прямой луч отсутствует (NLOS) =0 – закон Рэлея.

Многолучевой канал – это канал связи с рассеянием энергии сигнала во времени:

,

где 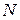- число лучей (путей распространения сигнала). Характеризуется профилем задержек (в модели для систем GSM =16 мкс).

Мобильный канал связи может быть описан с помощью модели Джейкса: скорость замираний определяется величиной доплеровского расширения спектра , ,

где - несущая частота сигнала, - скорость подвижного объекта (МС), =3*10⁸ м/с – скорость света, - угол между вектором движения МС и направлением прибытия -го луча (сигнала). Максимальный доплеровский сдвиг на частоте 2.4 ГГц составляет 10 Гц для пешеходов и 200 Гц для автомобилей (=100 км/ч).

Методы модуляции (BPSK, QPSK, 16QAM)

Рассмотрим формирование М-ичной PSK (фазовая манипуляция), где возможных сигналов имеют различные начальные фазы :

.

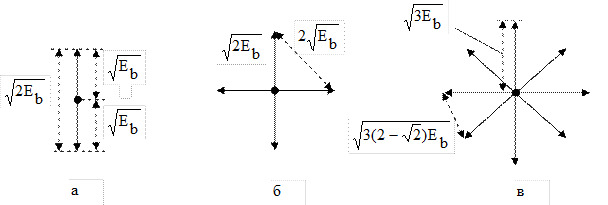
QPSK позволяет при сохранении помехоустойчивости (т.к. расстояние между соседними символами такое же как у BPSK 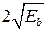) и ширины спектра (та же самая длительность элементарного символа – но уже несет в себе 2 бита), вдвое увеличить скорость передачи.

Вид модуляции	БФМ	КФМ, КФМС, p/4 – КФМ	МЧМ	Гауссовская МЧМ
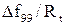
	18,5	9,2	1,2	0,92

Сигналы в методе модуляции M-QAM формируются с помощью следующего общего выражения:

где 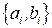- элементы матрицы 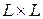элементов:

,

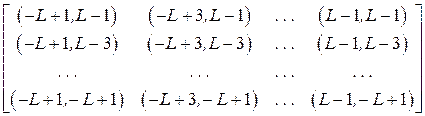где .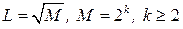

Принцип ортогонального частотного разделения каналов (OFDM)

OFDM-сигнал во временной области формируется с помощью ОБПФ (IFFT)

,

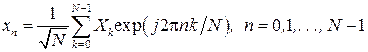где 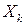- QAM-символ (в общем случае комплексное число на QAM-созвездии) в момент времени на -й несущей частоте.

OFDM-сигнал в частотной области формируется с помощью БПФ (FFT)

.

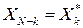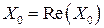, , , . При этом одна частота является центральной, относительно которой расположены по 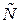частот.

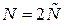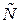, - половина несущих частот.

Условие ортогональности OFDM-сигналов:

,

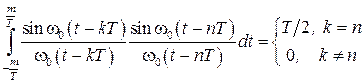где - длительность OFDM-символа на -й или 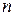-й частоте, .

Дата добавления: 2014-01-11