Пересечение поверхностей вращения

Лекция 11

Линией пересечения поверхностей является плоская или пространственная кривая, состоящая из:

- одного замкнутого контура, если одно геометрическое тело частично врезается в поверхность другого;

- распадается на несколько линий, если поверхность одного тела полностью пронизывает поверхность другого.

Рассмотрим особые случаи пересечения поверхностей вращения.

Цилиндрические, конические поверхности и однополосный гиперболоид вращения относятся к линейчатым поверхностям вращения второго порядка. Сфера, эллипсоид вращения, параболоид вращения и двухполосный гиперболоид вращения – нелинейчатые поверхностям второго порядка.

Поверхность второго порядка – множество точек пространства, декартовые координаты которых соответствуют алгебраическому уравнению второй степени.

.

Из аналитической геометрии известно, что порядок линии пересечения поверхностей равен произведению порядков поверхностей. Поэтому в общем случае две поверхности второго порядка (квадрики) пересекаются по пространственной линии четвертого порядка (биквадратной кривой), которая иногда распадается на несколько линий.

В некоторых частных случаях линия пересечения распадается на две плоские кривые второго порядка. Условия, при которых это возможно, определены в следующих теоремах. Зная их, можно быстрее и точнее построить линию пересечения поверхностей.

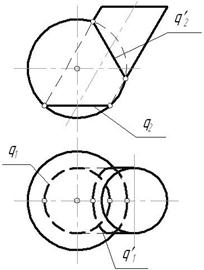
Рис. 6.19

Теорема 1:

Если две квадрики пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются.

Например, линия пересечения сферы и эллиптического цилиндра с круговым основанием распадается на две коники – окружности (q, q ¢).

Теорема 2:

Если две квадрики имеют касание в двух точках, то линия их пересечения распадается на две коники, плоскости которых проходят через отрезок прямой, соединяющей эти точки.

Рис. 6.20

Поверхности прямого кругового цилиндра и эллиптического цилиндра с круговым основанием имеют две общие точки касания (А, В). Следовательно, по Т2 они пересекаются по двум коникам – окружности (q) и эллипсу (q ¢), плоскости которых пересекаются по прямой АВ.

Теорема 3:

Две соосные поверхности вращения пересекаются по окружностям-параллелям, число которых равно числу точек пересечения главных полумеридианов поверхностей.

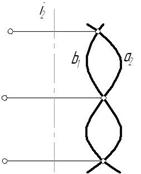
Рис. 6.21

Соосными называются поверхности, имеющие общую ось вращения.

Так как плоскость сечения перпендикулярна оси вращения i, линия сечения (окружность) проецируется:

- в окружность на плоскость, перпендикулярную оси i;

- в отрезок прямой – на плоскость, параллельную оси i;

- в эллипс – на любую другую плоскость.

Эти особенности соосных поверхностей вращения позволяют использовать их, в частности сферу, в качестве посредников при построении линии пересечения поверхностей вращения. Любая поверхность вращения, ось которой проходит через центр сферы, соосна с ней и, следовательно, пересекает ее по окружности.

Теорема 4 (Теорема Монжа):

Если две поверхности второго порядка (квадрики) описаны вокруг третьей квадрики, то они пересекаются по двум плоским кривым второго порядка (коникам).

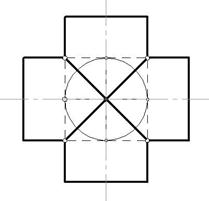
Рис. 6.22

В соответствии с этой теоремой, линии пересечения поверхностей, описанных около сферы, будут плоскими кривыми – эллипсами.

Построение линии пересечения поверхностей вращения в общем случае ведется с помощью дополнительных секущих поверхностей, в качестве которых могут быть использованы плоскости или сферы.

Секущие поверхности выбираются таким образом, чтобы с заданными поверхностями они пересекались по линиям, легко определяемым на КЧ.

Чтобы построить линию пересечения поверхностей на КЧ, необходимо:

1. Ввести ряд вспомогательных плоскостей или сфер, пересекающих обе заданные поверхности.

2. Построить линию пересечения каждой заданной поверхности со вспомогательной.

3. В месте пересечения построенных таким образом линий определить точки искомой линии взаимного пересечения.

4. Соединить полученные точки пересечения между собой с учетом видимости линии сечения.

Способ нахождения линии пересечения с помощью дополнительных плоскостей называется способом секущих плоскостей, а нахождение линии сечения с помощью дополнительных сфер – способом секущих сфер.

Каким бы способом не производилось нахождение линии пересечения, ее построение начинается с определения характерных точек сечения, а затем определяются промежуточные точки, необходимые для точности построения линии пересечения.

К характерным точкам линии пересечения относятся:

1. точки, проекции которых лежат на проекциях контурных образующих (очерках) заданных поверхностей;

2. «крайние» точки – правые и левые, наивысшие и наинизшие, ближайшие и наиболее удаленные.

Дата добавления: 2014-01-11