Пример 1.1. что означает, a порождает (состоит из)b

A ® b

или

a ::= b,

что означает, a порождает (состоит из) b.

Язык, порождаемый грамматикой ,- это множество цепочек, которые состоят только из терминалов и выводятся, начиная с одного, особо выделенного нетерминала S, называемого начальным символом или аксиомой грамматики. Среди множества правил грамматики должно присутствовать хотя бы одно правило:

S ® b.

Обозначение правил в форме записи x::= h относится к нотации Бэкуса – Наура (бэкусовой нормальной форме - БНФ). В этой нотации используются обозначения:

::= - это есть, ô- или;

[ ]- факультативный элемент (необязательная часть), то есть конструкция в скобках может присутствовать или отсутствовать во фразе языка;

{ }- множественный элемент (одно из, элемент выбора), то есть во фразе языка используется один из элементов внутри скобки.

Правило вида

a::=b ½ bg

можно представить

a::=b [ g ].

Бэкусовая нормальная форма (БНФ) или форма Бэкуса-Наура была предложена Д.Бэкусом в 1959 году и впервые применена П.Науром для описания языка Алгол-60. Метаязыком называется язык, который используется для описания других языков.

Правила вида x ® h являются порождающими, правила вида x ¬ h - распознающими.

Рассмотрим ряд грамматик и обсудим алгоритм порождения, применяемый для вывода цепочек языка.

<предложение>::=<подлежащее><группа сказуемого>

<подлежащее>::=мать ½ отец

<группа сказуемого>::=<сказуемое><дополнение>

<сказуемое>::=любит ½ обожает ½ боготворит

<дополнение>::=сына ½ дочь ™

Если имеется множество правил, то ими можно воспользоваться для того, чтобы вывести или породить цепочку (предложение) по следующей схеме. Начнем с начального символа грамматики - <предложение>, найдем правило, в котором <предложение> слева от::=, и подставим вместо <предложение> цепочку, которая расположена справа от::=, т.е.

<предложение> Þ <подлежащее> <группа сказуемого>

Таким образом, мы заменяем синтаксическое понятие на одну из цепочек, из которых оно может состоять. Повторим процесс. Возьмем один из нетерминалов в цепочке <подлежащее> <группа сказуемого>, например <подлежащее>; найдем правило, где <подлежащее> находится слева от::=, и заменим <подлежащее> в исходной цепочке на соответствующую цепочку, которая находится справа от::=. Это дает

<подлежащее> < группа сказуемого > Þ мать < группа сказуемого >

Символ " Þ " означает, что один символ слева от Þ в соответствии с правилом грамматики заменяется цепочкой, находящейся справа от Þ. Полный вывод одного предложения будет таким:

<предложение> Þ <подлежащее> <группа сказуемого>

Þ мать < группа сказуемого >

Þ мать <сказуемое> <дополнение>

Þ мать любит <дополнение>

Þ мать любит сына

Этот вывод предложения запишем сокращенно, используя новый символ Þ⁺

<предложение> Þ⁺ мать любит сына

На каждом шаге можно заменить любой нетерминал. В приведенном выше выводе всегда заменялся самый левый из них.

Вывод, на каждом шаге которого заменяется самый левый нетерминал сентенциальной формы, называется левым (левосторонним) выводом. Существует и часто используется также правый (правосторонний) вывод, который получается, если в сентенциальной форме заменять всегда самый правый нетерминал.

Обратите внимание на то, что предложенная грамматика используется для описания многих предложений. Девять правил грамматики, если считать каждую альтернативу за отдельное правило, а так оно и есть, определяют двенадцать предложений (цепочек) языка:

мать любит сына мать обожает сына мать боготворит сына

мать любит дочь мать обожает дочь мать боготворит дочь

отец любит сына отец обожает сына отец боготворит сына

отец любит дочь отец обожает дочь отец боготворит дочь

Одно из назначений грамматики как раз и состоит в том, чтобы описывать все цепочки языка с помощью приемлемого числа правил. Это особенно важно, если учесть, что количество предложений в языке чаще всего бесконечно.

Рассмотрим еще один пример полезной грамматики

Пример 1.2. Грамматики целого числа без знака содержат следующие 13 правил

(1) <число>::=<чс> S ® A

(2) <чс>::=<цифра><чс> A ® AB

(3) <чс>::=<цифра> A ® B

(4) <цифра>::=0 B ® 0

(5) <цифра>::=1 B ® 1

(6) <цифра>::=2 B ® 2

(7) <цифра>::=3 B ® 3

(8) <цифра>::=4 B ® 4

(9) <цифра>::=5 B ® 5

(10) <цифра>::=6 B ® 6

(11) <цифра>::=7 B ® 7

(12) <цифра>::=8 B ® 8

(13) <цифра>::=9 B ® 9

Заметим, что грамматики G(<число>) и G(S) определяют один и тот же язык и отличаются только именами нетерминалов и вторым правилом ™

А теперь продолжим наши определения.

Пусть G - грамматика. Будем говорить, что цепочка a непосредственно порождает цепочку b, и обозначим

a Þ b,

если для некоторых цепочек j и y можно написать

a = jUy

b = jgy,

где

U::= g

правило грамматики G. Будем также говорить, что b непосредственно выводима из a или что b непосредственно приводится (редуцируется, сворачивается) к a.

Цепочки j и y, конечно, могут быть пустыми. Следовательно, для любого правила A®a грамматики G имеет место A Þ a. На рис. 1.1 даны некоторые примеры непосредственных выводов для грамматики G(<число>) из примера 1.2 и обозначений предыдущего определения.

Будем говорить, что a порождает b или b приводится к a и записывать a Þ⁺ b, если существует последовательность непосредственных выводов

a = g₀ Þ g₁ Þ g₂ Þ... Þ g_n = b,

где n>0. Эта последовательность называется выводом длины n. Будем писать a Þ ^* b, если a Þ⁺ b или a = b (рис.1.1).

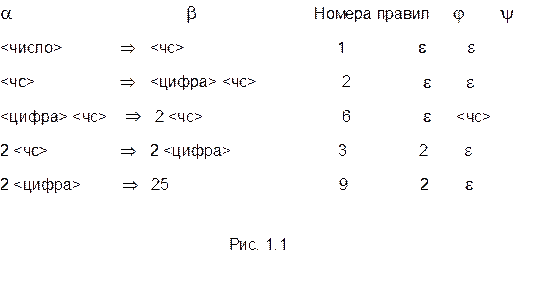
Если просмотреть все строки рис 1.1, то мы получим:

<число> Þ <чс> Þ <цифра> <чс> Þ 2 <чс> Þ 2 <цифра> Þ 25.

Таким образом, <число> Þ⁺ 22 и длина вывода равна 5. (Если длина вывода известна, можно записывать в явном виде <число> Þ⁵ 22).

Заметим, что пока в цепочке есть хотя бы один нетерминал, из нее можно вывести новую цепочку. Однако если нетерминальные символы отсутствуют, то вывод завершен. Неслучайно " терминалом " (terminal - заключительный, конечный) называют символ, который не встречается в левой части ни одного из правил. Исключение составляют нетерминалы-тупики, которые будут рассмотрены позже.

Цепочка a называется сентенциальной формой, если a выводима из начального символа S, т.е. если

SÞ ^* a.

Цепочка языка - это сентенциальная форма, состоящая только из терминалов.

Язык L(G(S)) - это множество цепочек:

L(G)={ a ç SÞ ^* a и aÎV_T ^* },

т.е. язык - это подмножество множества всех терминальных цепочек V_T ^*.

Структура цепочек языка задается грамматикой и, как видно из примера 1.2, несколько грамматик могут определять один и тот же язык. Такие грамматики называются эквивалентными.

Пусть G(S) - грамматика. И пусть w =abg - сентенциальная форма. Тогда b называется фразой сентенциальной формы w для нетерминального символа U, если S Þ ^* aUg и U Þ⁺ b; и далее, b называется простой фразой, если S Þ ^* aUg и U Þ g.

Тот факт, что U Þ⁺ b, вовсе не означает, что b является фразой сентенциальной формы abg; необходимо также иметь S Þ ^* aUg. Значит ли в примере 1.2, что <чс> является фразой сентенциальной формы 1 <чс>, если существует правило <число>::=<чс>? Конечно, нет, поскольку невозможен вывод цепочки 1 <число> из начального символа грамматики <число>. Каковы же фразы сентенциальной формы 1 <чс>? Имеет место вывод:

<число> Þ <чс> Þ <цифра><чс> Þ 1<чс>

Таким образом,

(1) <число> Þ ^* <чс> и <чс> Þ⁺1<чс>

(2 ) <число> Þ ^* <цифра><чс> и <цифра> Þ⁺1

Следовательно, 1<чс> и 1 - фразы, простой же фразой будет только 1.

В дальнейшем мы часто будем говорить о самой левой простой фразе сентенциальной формы, которая называется основой.

Грамматики G(<число>) и G(S) из примера 1.2 описывают бесконечный язык, т.е. язык, состоящий из бесконечного числа цепочек. Это обусловлено тем, что правило <чс>::=<цифра><чс> (A®AB) содержит <чс> (A) и в левой, и в правой частях, т.е. в некотором смысле символ <чс> (A) сам себя определяет.

В общем случае, если U Þ⁺...U..., то говорят, что грамматика рекурсивна по отношению к U. Если U Þ⁺ U..., то имеет место левая рекурсия, а если U Þ⁺...U, то - правая рекурсия. Соответствующие правила называют лево- (право)рекурсивными. Если язык бесконечен, то определяющая его грамматика должна быть рекурсивной.

Ниже представлен пример грамматики, которая включает правило с двухсторонней рекурсией.

Пример 1.3. Грамматика идентификатора, то есть последовательности из одного или более символов, начинающейся с буквы, и содержащей буквы и цифры в качестве возможного продолжения

S ® AB

A ® a A ® b

.............................

A ® y A ® z

B ® BB B ® e

B ® A B ® 0

..............................

B ® 9. ™

Дата добавления: 2014-01-11