Эквивалентность недетерминированных и детерминированных

А-грамматик

Термин недетерминированный автомат может привести в недоумение, так как в русском и других языках понятие автомата, в сущности, не позволяет применить к нему прилагательное “недетерминированный”. Недетерминированный автомат - это формализм для определения множества цепочек, обобщающий понятие конечного автомата (ни о каких случайностях, вероятностях здесь речи нет).

Недетерминированный автомат (НДА) - это автомат, где значение функции переходов d - не отдельное состояние, как в детерминированном автомате (ДА), а множество состояний. В общем случае у НДА может быть также не одно, а множество начальных состояний (если начальное состояние не единственно, то эти состояния при изображении таблицы переходов будут помечаться стрелкой).

НДА изучается, так как для заданного множества иногда легче найти недетерминированное описание.

Говорят, что НДА допускает входную цепочку, если он позволяет связать одно из его начальных состояний с одним из допускающих.

Так автомат, представленный на рис. 3.2, допускает цепочку 11, так как

,

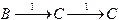причем В - начальное, а С - допускающее состояния. Существование одной этой последовательности достаточно, чтобы показать допустимость входной цепочки 11 и существование другой последовательности

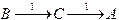, где A - отвергающее на это не влияет.

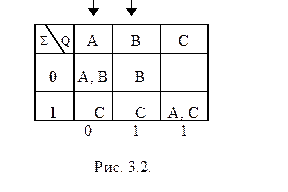
На рис. 3.3 представлен еще один НДА с входным алфавитом { а, л, н, о, с, ь }, который допускает только две цепочки лассо и лань.

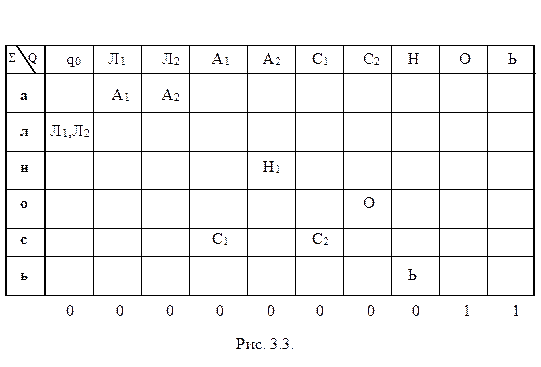
Понятие НДА приобретает практическое значение, так как для каждого НДА существует эквивалентный ему ДА, то есть ДА, допускающий в точности те же цепочки, что и НДА.

Основная идея построения ДА по НДА заключается в том, что после обработки отдельной входной цепочки состояние ДА будет представлять собой множество всех состояний НДА, которые он может достичь из начальных состояний после применения данной цепочки. Переходы ДА можно получить из НДА, вычисляя множества состояний, которые могут следовать после данного множества при различных входных символах. Допустимость цепочки определяется исходя из того, является ли последнее детерминированное состояние, которого достиг ДА, множеством недетерминированных состояний, включающим хотя бы одно допускающее состояние. Результирующий ДА будет иметь конечное множество состояний, так как число подмножеств состояний НДА конечно. В общем случае, если НДА содержит n состояний, то ДА будет содержать 2 ⁿ состояний. На практике многие из этих подмножеств представляют собой недостижимые состояния.

В приведенной ниже процедуре перехода от НДА к ДА переходы строятся только для тех подмножеств, которые действительно необходимы.

Пусть М_н - НДА, а М_д - эквивалентный ему ДА. Процедура перехода от НДА к ДА задается пятью шагами.

1. Пометить первый столбец функциональной таблицы для М_д множеством начальных состояний автомата М_н. Применить к этому множеству шаг 2.

2. По данному множеству состояний X, помечающему столбец таблицы переходов М_д, для которого переходы еще не вычислены, определить те состояния М_н, которые могут быть достигнуты из X с помощью каждого входного символа a, и поместить множества последующих состояний Y_a в соответствующие ячейки таблицы М_д. Символически это выражается так: если d функция НДА, то функция ДА d ^| задается формулой

d ^| (X,a) = {y | yÎ d (x,a), для некоторого x из X}.

3. Для каждого множества Y, порожденного переходами на шаге 2, определить, имеется ли уже в М_д столбец, помеченный этим множеством. Если нет, то создать новый столбец и пометить его этим множеством Y. Если множество Y уже использовалось как метка, то никаких действий не требуется.

4. Если в таблице М_д есть столбец, для которого переходы еще не вычислены, вернуться назад и применить к этому столбцу шаг 2. Если все переходы вычислены, перейти к шагу 5.

5. Пометить столбец как допускающее состояние М_д, когда он содержит допускающее состояние М_н. В противном случае пометить как отвергающее.

На рисунках 3.4 (а) и 3.5 представлены функциональные таблицы ДА, полученные по предложенному алгоритму из НДА с рисунков 3.2 и 3.3 соответственно. На рисунке 3.4 (б) та же таблица, что и на 3.4 (а), но с новыми именами состояний. Во всех этих таблицах пустая ячейка - не что иное, как ошибочное состояние.

Приведенный алгоритм можно использовать и для перехода от недетерминированной А-грамматики к детерминированной.

Пример 3.1. Пусть задана недетерминированная А-грамматика вида

S ® aB ï aC ï bB ï bS ï c

B ® cC ï c

C ® a ï aS ï c

Эта грамматика не имеет естественного символа, ограничивающего цепочку, поэтому во всех правилах вида A ® a добавим предзаключительное состояние F^½ и получим правила A ® a F^½

Добавим также символ ограничения цепочки, например ^ и правило

F^½ ® ^ F, где F - заключительное состояние. В результате получим модифицированную грамматику:

S ® aB ï aC ï bB ï bS ï cF^½

B ® cC ï cF^½

C ® aF^½ ï aS ï cF^½

F^| ® ^ F

Рассматриваем для недетерминированных правил неупорядоченные безповторные достижимые подмножества множества нетерминалов и в результате получим детерминированную грамматику:

S ® a<BC> ï b<BS> ï cF^½

<BC> ® a<SF^½> ï c<CF^½>

<BS> ® a<BC> ï b<BS> ï c<CF^½>

<SF^½> ® a<BC > ï b<BS> ï cF^½ ï^ F

<CF^½> ® a<SF^½> ï cF^½ ï^ F

F^½ ® ^ F

Полученная грамматика порождает те же цепочки, что и исходная. Отметим, что дерево вывода в автоматной грамматике вырождено и его вполне можно представлять в виде строки. Так, дерево вывода цепочки acac ^ в исходной грамматике имеет вид

S _a B _c C _a S _c F^½ _^ F,

а в полученной детерминированной

S _a <BC> _c <CF^|> _a <SF^|> _c F^½ _^ F.

Отличие состоит в том, что каждый шаг порождения в детерминированной грамматике однозначен, что и определяет преимущество таких грамматик с точки зрения практического построения программ анализа по грамматике.

Можно переименовать нетерминалы сформированной детерминированной грамматики и получить грамматику в традиционной форме:

S ® aA ï bB ï cF^½

A ® aC ï cD

B ® aA ï bB ï cD

C ® aA ï bB ï cF^½ ï^ F

D ® aC ï cF^½ ï^ F

F^| ® ^ F •

Упражнения

3.1. Постройте детерминированные А-грамматики для следующих цепочек, завершающихся символом “;”:

(a) целых чисел без знака и беззначащих нулей;

(б) четных целых чисел без знака;

(в) идентификаторов, содержащих четное количество символов;

(г) для цепочек из упражнения 1.5.

3.2. Постройте конечный автомат, который будет распознавать слова go to, причем между ними может быть произвольное число пробелов, включая нулевое.

3.3. Постройте конечные распознаватели для описанных ниже множеств цепочек из нулей и единиц:

(а) число единиц четное, а нулей - нечетное;

(б) между вхождениями единиц четное число нулей;

(в) за каждым вхождением пары 11 следует 0;

(г) каждый третий символ - единица;

(д) имеется по крайней мере одна единица.

3.4. Постройте конечный автомат с входным алфавитом {0,1}, который допускает в точности такое же множество цепочек:

(а) все входные цепочки;

(б) все входные цепочки, кроме пустой;

(в) ни одной входной цепочки;

(г) входную цепочку 101;

(д) две входные цепочки: 01 и 0100;

(е) все входные цепочки, начинающиеся с 0 и заканчивающиеся на 1;

(ж) все цепочки, не содержащие ни одной единицы;

(з) все цепочки, содержащие в точности три единицы;

(и) все цепочки, в которых перед и после каждой единицы стоит 0;

3.5. Опишите словами множества цепочек, распознаваемых каждым из следующих автоматов (рис. 3.6):

Рис. 3.6

3.6. Постройте детерминированную А-грамматику по следующей недетерминированной:

S ® aA ï aB ï bB ï bD

A ® aB ï aS ï bD

B ® cS ï cB ï bD ï b

D ® dD ï dB ï bB ï bA ï a ï c

3.7. Опишите словами множества цепочек, распознаваемых каждым из недетерминированных автоматов, изображенных на рис. 3.7.

Рис. 3.7

3.8. Найдите детерминированный автомат, эквивалентный следующему недетерминированному (рис. 3.8):

Глава 4. ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ КОНТЕКСТНО-СВОБОДНЫХ И АВТОМАТНЫХ ГРАММАТИК

4.1. Декомпозиция правил грамматики.

4.2. Исключение тупиковых правил из грамматик.

4.3. Обобщенные КС-грамматики и приведение грамматик к удлиняющей форме.

4.4. Устранение левой рекурсии и левая факторизация.

Упражнения

4.1. Декомпозиция правил грамматики

Определение: две грамматики эквивалентны, если они порождают один и тот же язык. G₁~G₂, если L(G₁)=L(G₂).

Теорема: не существует алгоритма, определяющего эквивалентность или неэквивалентность двух грамматик, тем не менее, существуют такие преобразования исходных грамматик, которые приводят к новым грамматикам, не выходящим из класса грамматик, эквивалентных исходным.

Эту теорему примем без доказательства. Критериями преобразования грамматик, приведения к эквивалентным грамматикам являются следующие:

однозначность или детерминированность;

получение более короткого вывода цепочек;

исключение тупиковых правил.

В предыдущей главе была сформулирована теорема о существовании для любой А-грамматики эквивалентной ей грамматики во вполнедетерминированной форме и доказана первая часть теоремы, подтверждающая существование таких грамматик. Ниже будет доказана вторая часть теоремы, рассматривающая эквивалентность исходной А-грамматики и построенной.

Для доказательства эквивалентности исходной автоматной грамматики и построенной грамматики во вполне детерминированной форме необходимо доказать, что любая цепочка, принадлежащая языку L₁, выводится и в грамматике G₂, и наоборот: L₁=L_2,

если L(G₁) ÌL(G₂) и

L(G₂) ÌL(G₁).

Рассмотрим произвольную цепочку φ=a₁…a_k ÎL(G₁), тогда существует вывод этой цепочки вида: Sa1A1a2…akF.

Согласно построению, если в исходной грамматике существует правило вида S→aA₁, то в преобразованной грамматике будет правило вида <S>→a<..A₁…>.

Аналогично рассуждая для произвольного шага: если A_i→a_i+1 A_i+1,

то <..A_i..>→a_i+1<..A_i+1..>.

На последнем шаге вывода, имея в исходной грамматике правило вида A_k-1→a_kF, в преобразованной грамматике имеем правило <..A_k-1..>→a_k<..F..>, то есть существует последовательность шагов вывода:

<S>_a1 <..A₁…>.._ak<..F..> => φ ÎL(G₂).

В противоположную сторону рассуждения абсолютно аналогичны.

Пусть φ=a₁…a_k ÎL(G₂). Отсюда следует, что существует вывод этой цепочки в языке, порождаемом грамматикой G₂, то есть существует вывод цепочки:

<S>_a1 <..A₁…>.._ak<..F..>.

По построению, если существует правило вида <S>→a₁<..A₁…>, то в исходной грамматике существует правило вида S→a₁ A₁.

Рассуждая аналогично, имея правило вида <..A_k-1..>→a_k<..F..> в исходной грамматике, имеем правило вывода A_k-1→a_kF, то есть φ ÎL(G₁) и отсюда следует, что L(G₂) ÌL(G₁), откуда L₁=L₂. Что и требовалось доказать.

Следующие теоремы позволяют обосновать возможность эквивалентных преобразований, приводящих к грамматикам с большим количеством правил, но вывод в которых короче.

Пусть дана КС-грамматика G₁=(V_N,V_T, R, S).

Теорема 4.1. Если в КС-грамматике G₁ существуют правила Y®aXb и X®g, то грамматика G₂=(V_N, V_T,R È { Y®agb},S) эквивалентна G₁.

Доказательство. Проверим, что любая цепочка, выводимая в одной грамматике, выводима и в другой.

Пусть j Î L(G₁), тогда дерево вывода j в G₁ является деревом вывода j и в G₂. Обратно, пусть j Î L(G₂), следовательно существует некоторое дерево вывода j в G₂. Если при этом правило Y®agb не используется, то дерево вывода j в G₂ является деревом вывода j в G₁. Если же правило Y®agb использовалось при выводе j в G₂, то фрагмент вывода Y Þ agb заменяем на фрагмент

Y Þ aXb Þ agb.

В результате получим дерево, в котором используются правила только из P, то есть получим вывод цепочки в G₁. Следовательно, из j Î L(G₂) следует, что j Î L(G₁). 

Теорема 4.2. Пусть в грамматике G₁ имеется множество правил

{Y® a Xb, X® g₁, X® g₂,..., X® g_n}.

Тогда, заменив это множество на множество

{Y® ag₁b, Y® ag₂b,..., Y® ag_nb, X® g₁, X® g₂,... X® g_n},

получим грамматику, эквивалентную G₁. И далее, если X ¹ S и других правил, которые имеют X в правой части, нет, то группу правил X® g _k,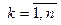 можно удалить.

Доказательство. Многократно применяя теорему 4.1 в грамматику добавляем правила Y® ag_kb, где 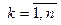. Удаление правила Y® aXb не приводит к потере выводимых цепочек, так как фрагмент дерева вывода Y Þ aXb Þ ag_kb можно заменить на YÞ ag_kb. ƒ

Пример 4.1. Рассмотрим фрагмент грамматики для описания числа

<число> ® <знак> <чбз>

<знак> ® + ½ -½ e

Здесь в соответствии с теоремой 4.2: Y - <число>, a - пустая цепочка, X - <знак>, b - <чбз> (число без знака), g₁ - +, g₂ - -, g₃ - e. Группу приведенных правил заменяем на правила

<число> ® + <чбз> ½- <чбз> ½ <чбз> ƒ

Теорема 4.3. Замена группы правил Y₁® a ₁Xb ₁ , Y₂® a ₂Xb ₂ ,... Y_m® a _mXb_m, X® g на правила Y₁® a ₁gb ₁ , Y₂® a ₂gb ₂ ,... Y_m® a _mgb _m, X® g, где других правил с нетерминалом X в левой части нет, приводит к эквивалентной грамматике. Если X ¹ S и других правил, которые имеют X в правой части, нет, то правило X® g можно удалить.

Доказательство здесь аналогично теореме 4.2. ƒ

Пример 4.2. Замена правил:

S ® AB.C ½ AB. ½ A.C ½ B. ½ .C

A ® -

на правила:

S ® -B.C ½ -B. ½ -.C ½ B. ½ .C

приводит к эквивалентной грамматике. ƒ

Теорема 4.4. Декомпозиция правил. Замена в грамматике G₁ группы правил

на группу правил 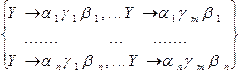, если

и других в левых и правых частях правил грамматики нет, приводит к грамматике, эквивалентной G₁.

При декомпозиции n+m правил грамматики заменяется на n * m правил. ƒ

Пример 4.3. Рассмотрим КС - грамматику идентификатора, имеющую вид:

<И> ® <Б> ½ <Б> <И₁>

<И₁> ® <Б> ½ <Б> <И₁> ½ <Ц> ½ <Ц> <И₁>

<Б> ® a ½ b ½ c ½ ... ½ y ½ z

<Ц> ® 0 ½ 1 ½ 2 ½ ... ½ 8 ½ 9

В предложенной грамматике 42 правила. Проведем в ней декомпозицию по <Б> и по <Ц>. Получим новую грамматику, эквивалентную заданной.

<И> ® a ½ ... ½ z ½ a <И₁> ½ ... ½ z <И₁>

<И₁> ® a ½ ... ½ z ½ a <И₁> ½ ... ½ z <И₁> ½ 0 ½...½ 9 ½ 0<И₁> ½ ... ½ 9<И₁>

В результате получено 4*26=104 правил для букв и 2*10=20 правил для цифр, итого 124 правила. Правил стало больше, но вывод, а следовательно и разбор, будет короче. Нетрудно видеть, что рассмотренная декомпозиция позволила перейти от КС-грамматики идентификатора к А-грамматике. ƒ

Отметим в заключение параграфа, что все рассмотренные теоремы работают в обе стороны. Так n * m правил при композиции можно заменить на n+m правил. Иногда лучше иметь правил поменьше и компактно описывать язык; иногда, с целью повышения эффективности разбора, их количество необходимо увеличить.

4.2. Исключение тупиковых правил из грамматик

Правило A® j By называется внешним тупиком, если не существует правила B®x. (Из нетерминала B нет выхода).

Правило B® x называется внутренним тупиком, если B ¹ S и не существует правила A® j By. (Нетерминал B не может появиться ни в одной сентенциальной форме, выводимой из начального символа грамматики. Внутренний тупик - это аналог недостижимого состояния конечного автомата).

Циклический тупик - это группа правил вида

A₀® j₁A₁y₁

A₁® j₂A₂y₂

..................

A_n® j₀A₀y₀,

где A_i ¹ S и, при этом, либо для любого A_i не существует правил вида B® lA_im (циклический тупик внутреннего типа), либо для любого A_i не существует правил вида A_i®c (циклический тупик внешнего типа). ƒ

Теорема 4.5. Для любой грамматики существует эквивалентная ей грамматика без тупиков.

Для доказательства данной теоремы достаточно вспомнить, что эквивалентные грамматики порождают один и тот же язык (множество терминальных цепочек, которое выводятся из начального символа грамматики). Очевидно, что правила, включающие тупики, при порождении терминальных цепочек из начального символа грамматики просто не могут использоваться.

Алгоритмы поиска тупиков и их устранения рассмотрим на примере.

Пример 4.4. Пусть задана грамматика c начальным символом S и следующим множеством правил

S® a A ½ c C ½ b D ½ q P ½ k T A® c C

C® k T® m

D® b T ½ f K P® c R

R® d K B® d Q ½ m

Q® p B ½ r B

Здесь выбрана автоматная грамматика только для того, чтобы наглядно проиллюстрировать ее графом состояний (рис. 4.1).

Построим новую грамматику, отбирая из исходной “хорошие” (производящие нетерминалы), из которых выводится терминальная цепочка.

Для этого положим, что множество

X₀ = V_T,

то есть X₀ совпадает с множеством терминалов.

X₁ = { A | $ A® x, где xÎ X_o },

то есть те нетерминалы, из которых терминальная цепочка получается за один шаг.

X₂ = { A | $ A® x, где xÎ (X_o È X₁) },

.......................................................

X_i = { A | $ A® x, где xÎ },

то есть X_i - множество нетерминалов, из которых терминальная цепочка получается не более чем за i шагов (под шагом здесь понимается одновременная замена всех нетерминалов сентенциальной формы). На каждом шаге мы добавляем новые нетерминалы, их конечное число, - следовательно конечен и данный процесс (X₁ Í X₂ Í... X _i Í V_N).

Положим Z _i равным разности X _i и X _i-1, Z _i = X _i \ X _i-1 -

это те нетерминалы из которых терминальная цепочка получается ровно за i шагов. Если Z _i = Æ - пустое множество, то процесс формирования продуктивных нетерминалов пора закончить, так как из Z _i = Æ следует, что

Z _i+1 = Æ и т.д.

Отобранные нетерминалы обладают тем свойством, что из них выводятся терминальные цепочки. Оставшиеся нетерминалы терминальных цепочек не порождают и их можно удалить из грамматики вместе с правилами, содержащими их в левой или правой части. Этот алгоритм позволяет устранить все внешние тупики и циклические тупики внешнего типа.

В рассматриваемом примере

X₀ = {a,c,b,q,k,m,f,d,p,r},

X₁ = {C,T,B}, Z₁ = {C,T,B},

X₂ = {S,A,C,T,D,Q,B}, Z₂ = {S,A,D,Q}

X₃ = {S,A,C,T,D,Q,B}, Z₃ = Æ.

Следовательно X₃ - и есть то самое множество “хороших” нетерминалов. Удалив остальные нетерминалы и все ссылки на них в правилах грамматики, мы получим грамматику:

S® a A ½ c C ½ b D ½ k T A® c C

C® k T® m

D® b T B® d Q ½ m

Q® p B ½ r B

Для устранения внутренних тупиков повторим процесс выбора “хороших” символов с другого конца. Положим

Y₀ = { S },..., Y _i = { A | $ B® jAy, где AÎ (V_TÈ V_N) и BÎ Y _i-1 },

то есть Y _i - множество символов (терминалов и нетерминалов), которые могут появиться в сентенциальной форме на i - том шаге вывода.

В нашем примере

Y₀ = {S},

Y₁ = {a,A,c,C,b,D,k,T},

Y₂ = {c,C,k,m,b,T}, Y₃ = {k,l}.

Далее, определим

W _i = Y _i \ () Ç V_N,

то есть новые нетерминалы, появляющиеся на i - том шаге. Очевидно, что из

W _i = Æ следует, что процесс можно закончить, так как все нетерминалы, выводимые из начального символа грамматики, уже получены. Остальные нетерминалы и содержащие их правила грамматики можно удалить.

В нашем случае

W₀={S},

W₁={A,C,D,T},

W₂=Æ.

Нетерминалы B и Q - внутренние тупики. Таким образом, грамматика без тупиков имеет вид:

S® a A ½ c C ½ b D ½ k T A® c C

C® k T® m D® b T ƒ

Дата добавления: 2014-01-11