
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрические и кинематические характеристики механизма
|
|
|
|
ТЕМА: Кинематический анализ механизмов.
ЛЕКЦИЯ 4
Краткое содержание: Кинематические передаточные функции (аналоги линейных и угловых скоростей и ускорений)и кинематические характеристики механизмов. Связь кинематических и передаточных функций. Задачи и методы кинематического анализа. Кинематический анализ методом кинематических диаграмм.
Кинематические передаточные функции и кинематические характеристики механизмов
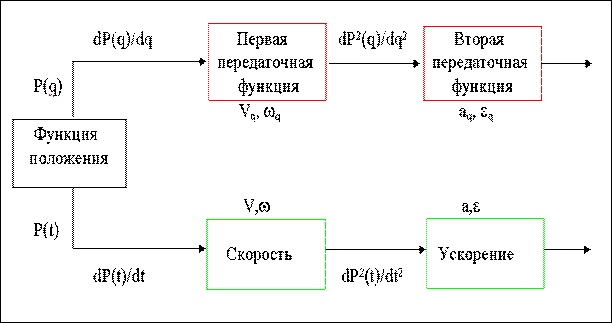
Функцией положения механизма называется зависимость углового или линейного перемещения точки или звена механизма от времени или обобщенной координаты.
|
| Рис. 4.1 |
Кинематическими передаточными функциями механизма называются производные от функции положения по обобщенной координате. Первая производная называется первой передаточной функцией или аналогом скорости (обозначается Vq,ωq), вторая - второй передаточной функцией или аналогом ускорения (обозначается а q, εq).
Кинематическими характеристиками механизма называются производные от функции положения по времени. Первая производная называется скоростью (обозначается V, ω), вторая - ускорением (обозначается a, ε).
Механизм с одной подвижностью имеет одно заданное входное движение и бесчисленное множество выходных (движение любого звена или точки механизма). Передаточные функции тех движений, которые в данном случае используются как выходные, называются главными, остальные - вспомогательными.
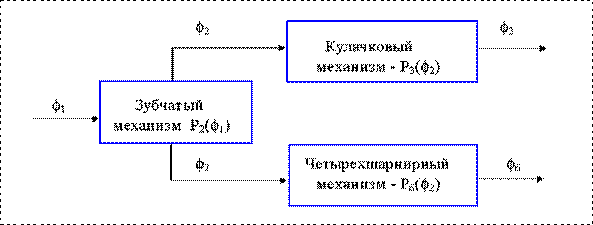
Рассмотрим схему механической системы образованной последовательно-параллельным соединением типовых механизмов. Схема включает входное звено, зубчатую передачу, кулачковый и рычажный механизмы и имеет два выходных звена.
Схема механической системы

| ||
| Рис. 4.2 | ||
| ||
| Рис. 4.3 Функции положения в механизмах | ||

| ||
| Рис. 4.4 | ||
Связь кинематических характеристик и передаточных функций
Линейные скорости и ускорения
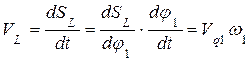
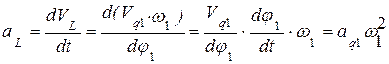
Угловые скорости и ускорения.
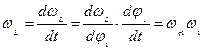
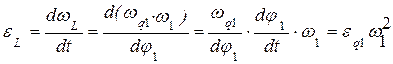
Задачи и методы кинематического исследования механизмов
Кинематическое исследование механизма состоит в изучении движения звеньев без учета сил, действующие на эти звенья, при заданном движении ведущего звена.
Кинематический анализ выполняется по кинематической схеме механизма. Он состоит в определении кинематических характеристик:
1) перемещений звеньев и траекторий, описываемых характерными точками звеньев (например, центра масс звена);
2) линейных скоростей и ускорений точек звеньев;
3) угловых скоростей и ускорений звеньев.
Кинематический анализ позволяет установить соответствие кинематических характеристик (перемещений, скоростей и ускорений) заданному закону движения механизма, а также получить исходные данные для выполнения динамического анализа. По полученным кинематическим характеристикам определяют инерционные нагрузки звеньев, кинетическую энергию механизма, закон движения ведущего и ведомых звеньев в функции времени.
Известны следующие методы кинематического анализа:
- планов положений, скоростей и ускорений,
- проекций векторного контура,
- кинематических диаграмм,
- центроид,
- преобразования координат,
- экспериментальный.
Кинематическое исследование проводят графическим и аналитическим методами. Графическое определение кинематических параметров основано на геометрических построениях, погрешность результатов которых составляет (0,3-0,5)% по сравнению с аналитическими расчетами. Графический метод нагляден и универсален, так как позволяет определять положения, скорости и ускорения звеньев механизма любой структуры. Метод построения планов скоростей и ускорений применяется при инженерных расчетах, как при анализе, так и при синтезе механизмов. Графический метод построения кинематических диаграмм позволяет использовать при анализе заданные в виде графиков законы изменения кинематических параметров в функции обобщенных координат φ и t. Точность графических методов достаточна для выполнения технических расчетов. Если требуется проводить расчеты с высокой точностью, применяют аналитические методы, применение ЭВМ в этом случае упрощает расчеты.
Метод цикловых кинематических диаграмм (кулачковые механизмы).
Кулачковым называется трехзвенный механизм, состоящий из двух подвижных звеньев - кулачка и толкателя, соединенных между собой высшей кинематической парой. Часто в состав механизма входит третье подвижное звено - ролик, введенное в состав механизма с целью замены в высшей паре трения скольжения трением качения. При этом механизм имеет две подвижности одну основную и одну местную (подвижность ролика).
Основные параметры кулачкового механизма:
 раб - фазовый рабочий угол кулачкового механизма;
раб - фазовый рабочий угол кулачкового механизма;
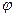 раб =
раб = 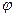 c +
c + 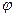 дв +
дв + 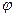 у;
у;
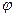 с - угол сближения;
с - угол сближения;
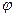 дв - фазовый угол дальнего выстоя;
дв - фазовый угол дальнего выстоя;
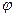 у - фазовый угол удаления;
у - фазовый угол удаления;
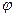 бв - угол ближнего выстоя;
бв - угол ближнего выстоя;
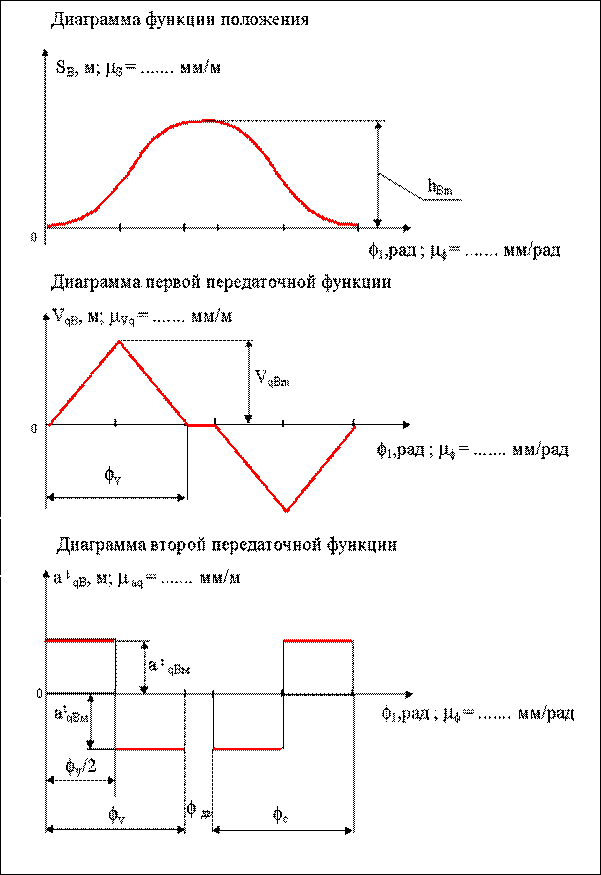
hBm - максимальное перемещение точки В толкателя;
r0 - радиус начальной шайбы кулачка;
rр - радиус ролика.
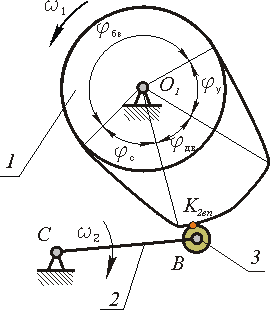
Рис. 4.5
При кинематическом анализе кулачкового механизма задан конструктивный профиль кулачка и радиус ролика rp. Методом обращенного движения (перекатывая ролик по неподвижному конструктивному профилю кулачка) находим центровой профиль кулачка (траекторию центра ролика толкателя в обращенном движении). Наносим на профиль фазовые углы и определяем в зоне ближнего выстоя начальный радиус центрового профиля кулачка r0. В зоне рабочего угла проводим ряд траекторий центра ролика толкателя (точки В) и по ним измеряем от точки лежащей на окружности r0 до точки лежащей на центровом профиле текущее перемещение толкателя SBi. По этим перемещениям строим диаграмму SB = 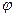 (
( 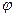 1). Дифференцируя эту диаграмму по времени или обобщенной координате, получаем кинематические или геометрические характеристики механизма. При графическом дифференцировании масштабы диаграмм зависят от масштабов исходной диаграммы и выбранных отрезков дифференцирования:
1). Дифференцируя эту диаграмму по времени или обобщенной координате, получаем кинематические или геометрические характеристики механизма. При графическом дифференцировании масштабы диаграмм зависят от масштабов исходной диаграммы и выбранных отрезков дифференцирования:

Рис. 4.6
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2114; Нарушение авторских прав?; Мы поможем в написании вашей работы!