Числовые характеристики генеральной совокупности

Числовые характеристики представления статистического ряда.

Для достоверной оценки качества продукции помимо графиков необходимы некоторые числовые значения, отражающие существенные характеристики ряда. Они делятся на характеристики положения и характеристики рассеивания.

Характеристиками положения являются:

1. Среднее арифметическое

2. Медиана (Ме). Если полученные при измерениях значения расположить в возрастающем или убывающем порядке, то среднее по положению число будет называться медианой. При n=2m+1 Me=x_m+1, n=2m Me=(x_m+x_m+1)/2. Значение медианы легко получить по кумулятивной кривой.

3. Мода (Мо). Значение параметра, наиболее часто встречающегося в рассматриваемом ряду. (1,2,7,2,5,12,2,7 -> Мо=2). В случае непрерывного распределения при равных интервалах Мо соответствует интервалу с наибольшей частотой. А в случае неравных интервалов, тому, плотность которого максимальна. Плотность высчитывают как отношение относительной частоты к длине интервала.

Характеристики положения не учитывают то, как случайные величины распределяются в диапазоне своих значений, поэтому в мат.статистике используют характеристики рассеивания.:

Размах R=хmax-xmin. Величина не устойчивая, зависящая от случайных обстоятельств, поэтому её применяют для приближенной оценки рассеивания или для выборки малого объема.

Более устойчивыми параметрами являются дисперсия (S² ) и СКО (S). Дисперсия и СКО показывают как тесно группируются отдельные значения вокруг среднего арифметического. СКО иногда называют стандартным отклонением.

Коэффициент вариации – отношение стандартного отклонения к среднему арифметическому, выраженное в процентах. Этот коэффициент показывает относительные колебания случайной величины вокруг среднего арифметического.

Характеристикой положения генеральной совокупности является математическое ожидание или генеральное среднее арифметическое значение случайной величины.

1. Математическое ожидание

Характеристики рассеивания:

2. Дисперсия с.в.

3. СКО

Для характеристики вида кривых распределения используются оценки, основанные на центральных моментах. Характеристики вида и симметричности кривой распределения оцениваются:

1. Центральным моментом 3-го порядка, который служит оценкой асимметрии. Мз = .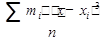

2. Мера асимметрии (косость кривой распределения) A= Мз/σ³. Для числовых рядов – коэффициент асимметрии a=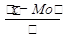. Для симметричных распределений 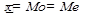→ a=0.

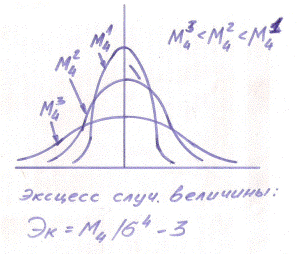
3. Крутость (островершинность) кривой распределения оценивается центральным моментом 4-го порядка. .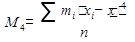

Эксцесс случайной величины используют для характеристики крутости. Определяется сравнением с кривой нормального распределения.

Основные законы распределения случайных величин, наиболее широко применяемые в системах УК.

1. Равновероятный закон распределения. Случайная величина Х распределена по равномерному закону, если плотность её распределения определена следующим образом:

Кроме плотности вероятности для непрерывных распределений используется также интегральная форма распределения. Физический смысл интегральной функции распределения состоит в том, что она представляет собой вероятность попадания случайной величины в диапазон от -∞ до Х. Равновероятным законом можно описать распределение случайной величины при равномерном «уходе» одного из параметров ТП.

2. Закон нормального распределения. Согласно центральной предельной теореме теории вероятности, распределение любой совокупности случайных величин, если число их велико и отсутствуют превалирующие факторы, в пределе стремится к Гаусовскому (нормальному). Существует 3 условия центральной предельной теоремы:

1. Случайные величины должны быть независимы или слабо зависимы;

2. Их число должно стремиться к бесконечности;

3. Среди совокупности случайных величин должны отсутствовать такие, СКО которых сильно отличается.

Можно утверждать, что, если ТП отлажен и контролируем, то распределение отклонения ПКИ на каждой ТО будет близко к нормальному.

Плотность распределения вероятностей описывается законом Гауса. Кривая плотности распределения:

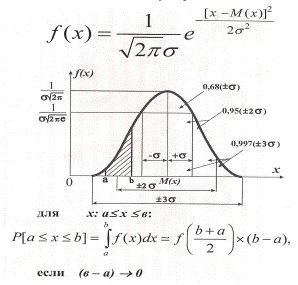По известной плотности распределения значений параметров можно определить вероятность того, что величина параметра попадет в интервал ab. Для более точного определения вероятности попадания случайной величины в интервал от а до b используется табличная функция Лапласа или интеграл вероятности.

При изменении Mх кривая смещается вправо/влево вдоль оси х. При изменении СКО изменяется крутость кривой. Чем меньше сигма, тем кривая круче.

На практике, зная мат.ожидание и СКО параметров качества изделия можно приблизительно указать интервал изменения ПКИ. При этом, вероятность появления значения за пределами зоны в 6сигма можно считать практически невозможным.

Если на ТП воздействует ряд независимых случайных факторов Х1,Х2..Хn с соответствующими плотностями распределения вероятностей f1(x)..fn(x), то мат.ожидание результирующей с.в. будет характеризоваться своими параметрами М(у)=∑М(хi) и σ²(У)=∑σ²(хi). Отсюда вытекает следствия:

1. Если дисперсии и мат.ожидания с.в. равны между собой, то результирующая дисперсия =. Коэффициент вариации для У – . Из этого выражения следует, что с ростом числа независимых случайных воздействий коэффициент вариации убывает и, следовательно, улучшается точность ТП.

2. Если 2 или более случайные величины имеют резко различающиеся СКО, то в результате совместного воздействия результирующую дисперсию в основном будет определять с.в. с большим СКО.

Дата добавления: 2014-01-11