Корреляционный анализ

Для управления любым ТП, любым оборудованием, машиной и пр. необходимо знать зависимость между входными и выходными параметрами.

Входные и выходные параметры можно представить как поток случайных величин. Рассматривая взаимосвязь `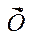и 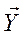, могут возникать следующие варианты:

1). 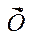и 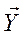тесно связаны между собой. Любому определенному значению х_i соответствует одно или несколько значений y_i. Зависимость между 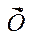и 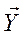выражается в виде формулы, а взаимосвязь называется функциональной (все точные законы физики, механики и т.д.).

2). 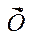и 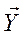не строго связаны между собой. Связь эта не функциональная, а статистическая, т.е. каждому значению х_i соответствует ряд изменяющихся вместе с изменением 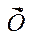значений 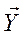и, наоборот, каждому значению y_i соответствует ряд значений 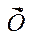, которые тоже изменяются с изменением .

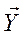3). 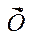и 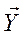не связаны между собой. В этом случае изменение 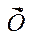или 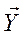не приводят к видимым изменениям 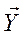или 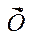соответственно.

На практике чрезвычайно важно знать не только зависят или нет 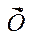и 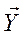, но и вид такой связи. Это очень важно для контроля и управления качеством ТП.

Учитывая, что при статистических связях каждому фиксированному значению одного признака соответствует распределение другого, можно представить эту связь в виде зависимости среднего арифметического значения одного из параметров, например, 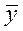, от другого. Это запишется так:

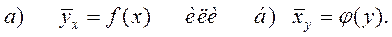(1)

Подобная запись отражает корреляционную связь параметров, а уравнения (1) называются уравнениями регрессии или корреляционными. Причем, 1а) – это уравнение регрессии 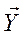на 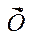, а 1б) – уравнение регрессии 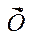на 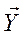. Вид функций j(y) и f(x) зависит от формы связи параметров.

На практике статистическую связь между двумя параметрами стараются находить в виде линейной функции или, если она нелинейная, ее сводят к линейной с помощью различных преобразований (логарифмирования, извлечения корня и т.п.). В крайнем случае, любая нелинейная функция может быть аппроксимирована кусочно-линейной функцией. Определение коэффициентов можно провести методом наименьших квадратов.

Если пары параметров обозначить через (x_i, y_i), i =1,…,n, то прямая регрессии 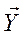на 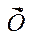запишется в виде:

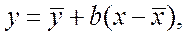(2)

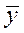где и 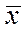– средние арифметические значений y_i и x_i, i = 1,…,n.

Коэффициент, называемый коэффициентом регрессии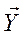на 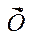, определяют по формуле:

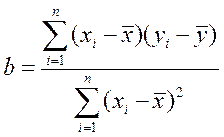(3)

Если рассматривать обратную зависимость, т.е. считать, что 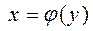, то прямая регрессии будет иметь вид:

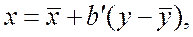(4)

а коэффициент регрессии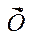на :

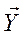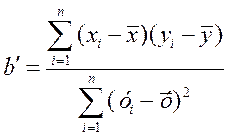(5)

Уравнения (2) и (4) не эквивалентны, так как b¢ ¹ 1 / b, т.е. прямая регрессии 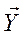на 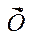не совпадает с прямой регрессии 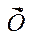на 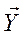, хотя обе они проходят через точку С с координатами .

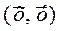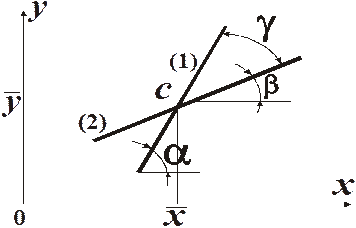
Очевидно, tga = b, b¢ = ctgb = 1 / tgb.

Полученные две прямые устанавливают взаимосвязь двух параметров. При этом в первом случае по известному значению х получаем оценку для у, а во втором – наоборот, по значению у получаем оценку для х.

Степень связи между параметрами х и у определяют коэффициентом корреляции r, вычисляемым по формуле:

(6)

Сравнивая с (3) и (5), получим:

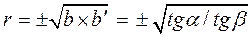
Отсюда: если прямые (1) и (2) совпадают, т.е. a = b, – связь функциональная, r = ± 1.

Если r = 1, то функциональная связь прямая (с ростом х растет у); если r = - 1 – то обратная (с ростом х у уменьшается).

Если |r| < 1, то связь между х и у статистическая. Причем, чем меньше |r|, тем связь слабее. На графике это отражается увеличением угла g. При g = 90° r = 0. Это соответствует отсутствию прямолинейной корреляционной связи между х и у, но это еще не значит, что отсутствует всякая корреляционная взаимосвязь, например, криволинейная.

Для оценки значимости самого коэффициента корреляции r учитывается число пар наблюдений n, по которым произведено его вычисление. При небольшом n для оценки применяют t – критерий (критерий Стьюдента), показывающий, случайно ли коэффициент корреляции отклоняется от нуля и имеется ли корреляционная связь между х и у. Для этого вычисляют:

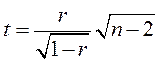
и сравнивают его с табличным значением. Если t £ t_табл, то корреляция между х и у существует.

В случае криволинейной связи между двумя потоками случайных величин корреляционная связь между ними устанавливается с помощью корреляционного отношения. Для этого из потока выбираются к выборок пар случайных величин х_ij и у_ij, i = 1, 2,…, k; j = 1, 2,…,n; для каждой из выборок вычисляются 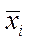и 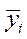, а также общие среднеарифметические 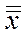и 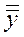и общие дисперсии s²(х) и s ²(у):

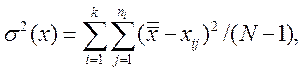
где 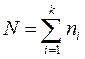– общий объем всех выборок.

Для s ²(у) формула аналогична.

Далее вычисляем корреляционные отношения:

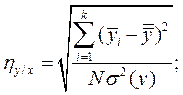(7)

для регрессии х на у:

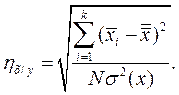(8)

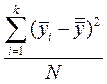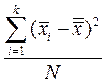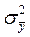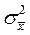Если учесть, что подкоренные выражения и есть ни что иное, как дисперсия средних арифметических около общих средних, т.е. и соответственно, то выражения (7) и (8) можно упростить:

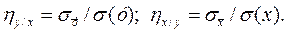
Величина корреляционного отношения меняется в пределах 0 £ h £ 1. Если х и у связаны функциональной связью, то h = 1. Если же какая-либо связь между ними отсутствует, то h = 0.

В любом случае значение корреляционного отношения не меньше абсолютного значения коэффициента корреляции, т.е. h ³ | r|. Если h = | r|, то это является необходимым и достаточным условием того, что связь между двумя рассматриваемыми величинами является линейной.

Дата добавления: 2014-01-11