Расслаивание потоков случайных величин с помощью дисперсионного анализа

Суммарный поток статистических данных, характеризующих качество изделия, как правило, характеризует также систематические и случайные погрешности. Особенно это характерно для производства, когда на ТП оказывают влияние множество независимых случайных воздействий (качество материала, температура, влажность, неоднородность растворов, настроение работника и т. д.), а также систематически изменяющихся (изменение концентрации растворов, изменение температуры, влажности и т. д.)

С другой стороны, известно, что получаемая в результате дисперсионного анализа оценка дисперсии внутри выборки () характеризует в основном случайную составляющую, а дисперсия между выборками (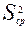)- систематическую.

Сравнивая дисперсию, обусловленную только одним каким-либо фактором (случайным или систематическим) с общей (суммарной) дисперсией, можно решить вопрос о значимости влияния этого фактора на общую дисперсию.

В качестве критерия значимости используется критерий Фишера (F-критерий). Если этот критерий подтвердит наличие превалирующего влияния какой-либо составляющей, то это значительно облегчит поиск источников нарушения ТП.

Рассмотрим, как это делается на примере.

Предположим, что мы в течение смены с одной технологической линии взяли 4 выборки транзисторов по 5 шт. в каждой и измерили статический коэффициент усиления по току (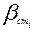). Генеральная совокупность, из которой сделаны выборки, подчиняется нормальному закону распределения с параметрами и . -случайная составляющая, а 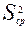-систематическая составляющая.

Таблица 2

№ транзистора в выборке	Номер выборок
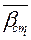
	51,6
	136,3	107,5	108,5
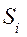
	11,67	10,37	10,42	10,49

Построим графики для и 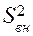(рис. 3):

k

Рис.3

Анализ графиков позволяет выдвинуть следующее предположение (гипотезу): сначала основные параметры ТП были расстроены – имелась систематическая ошибка и на ТП воздействовали значительные случайные факторы (), которые впоследствии были устранены (уменьшилась систематическая погрешность; и ), то есть в ТП превалирует какая-то погрешность: систематическая или случайная. Проверим, правильно ли наше предположение.

Определим:

Дисперсия внутри выборок:

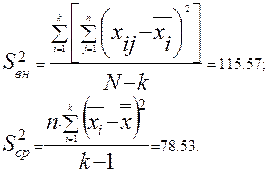
Определим причину такой большой разницы дисперсии, для чего воспользуемся критерием Фишера:

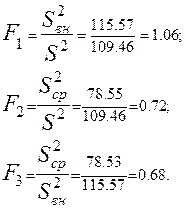
Из таблицы для и находим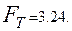

Т. к. 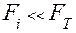, то это значит, что расхождение оценок дисперсий генеральной совокупности случайное, т. е. в ТП систематические погрешности не превалируют над случайными (это видно также из сравнения ). Если бы оказалось, что , то расхождение оценок дисперсий генеральной совокупности было бы неслучайным и, следовательно, в ТП превалировала бы какая-либо, например, систематическая погрешность.

В рассмотренном примере , что несколько не соответствует ТУ, поэтому превышение нормы у и 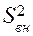следует искать среди источников случайных погрешностей.

Дата добавления: 2014-01-11