Пример 8.2

Дана квадратичная форма L(x_x, х₂) = 2х₁²+4x₁x₂-3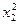. Найти квадратичную форму L(y₁,y₂), полученную из данной линейным преобразованием 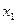= 2у₁ - 3y₂, x₂ = у₁ + у₂.

Решение.

Матрица данной квадратичной формы A=, а матрица линейного преобразования

С =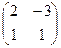. Следовательно, по (*) матрица искомой квадратичной формы

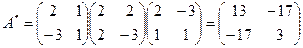, а квадратичная форма имеет вид

L(y_1, y₂) = .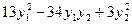

Следует отметить, что при некоторых удачно выбранных ли­нейных преобразованиях вид квадратичной формы можно суще­ственно упростить.

Определение. Квадратичная форма L(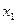,х₂,...,х_n) = 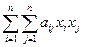называется канонической (или имеет канонический вид), если все ее коэффициенты 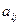= 0 при i¹j:

L=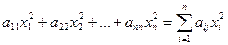, а её матрица является диагональной.

Справедлива следующая теорема.

Теорема. Любая квадратичная форма с помощью невырожден­ного линейного преобразования переменных может быть приведена к каноническому виду.

Пример 8.3

Привести к каноническому виду квадратичную форму

L(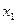, х₂, х₃) =

Решение.

Вначале выделим полный квадрат при перемен­ной 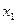, коэффициент при квадрате которой отличен от нуля:

Теперь выделяем полный квадрат при переменной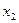, коэф­фициент при которой отличен от нуля:

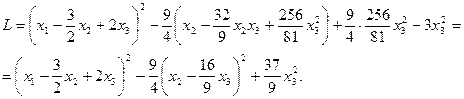
Итак, невырожденное линейное преобразование

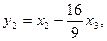
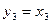приводит данную квадратичную форму к каноническому виду:

Канонический вид квадратичной формы не является одно­значно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способа­ми. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.

Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратич­ной формы не зависит от способа приведения формы к этому виду.

Следует отметить, что ранг матрицы квадратичной формы равен числу отличных от нуля коэффициентов канонической формы и не меняется при линей­ных преобразованиях.

Определение. Квадратичная форма L(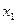, х₂,..., х_n) называется положительно (отрицательно) определенной, если при всех значениях перемен­ных, из которых хотя бы одно отлично от нуля,

L(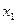, х₂,..., х_n) > 0 (L(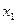, х₂,..., х_n) < 0).

Так, например, квадратичная форма 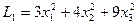явля­ется положительно определенной, а форма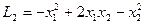- отрицательно определенной.

Теорема. Для того чтобы квадратичная форма L = Х'АХ была положительно (отрицательно) определенной, необходимо и доста­точно, чтобы все собственные значения, матрицы А были поло­жительны (отрицательны).

В ряде случаев для установления знакоопределенности квадра­тичной формы удобнее бывает применить критерий Сильвестра.

Теорема. Для того чтобы квадратичная форма была положи­тельно определенной, необходимо и недостаточно, чтобы все глав­ные миноры матрицы этой формы были положительны, т.е.

>0, > 0,...,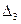>0, где

=

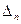Следует отметить, что для отрицательно определенных квадра­тичных форм знаки главных миноров чередуются, начиная со знака "минус" для минора первого порядка.

Дата добавления: 2014-01-11