Доказательство

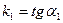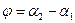Поскольку , и , то

.

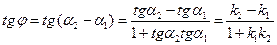Замечание. Если одна из прямых перпендикулярна оси 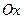(не существует один из угловых коэффициентов), то угол между прямыми вычисляется по формуле .

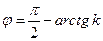Следствие. Из формулы (2.6) можно получить условия параллельности и перпендикулярности прямых. Пусть прямые заданы уравнениям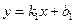и и 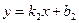. Если они параллельны, то 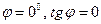и из формулы (2.6) следует, что . Если же они перпендикулярны, то не существует, а это возможно лишь в случае, когда .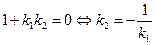

Теорема 2.7. Угол 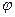между двумя прямыми, заданными уравнениям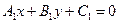и и 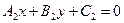, вычисляется по формуле

.

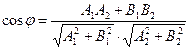Следствие. Пусть прямые заданы уравнениям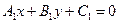и и 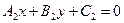. Если они параллельны, то 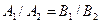; если они перпендикулярны, то .

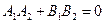Теорема 2.8. Расстояние от точки до прямой вычисляется по формуле

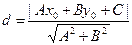. (2.7)

Пример 2.5. Две стороны параллелограмма заданы уравнениям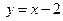и и 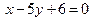, а его диагонали пересекаются в начале координат. Необходимо найти: а) острый угол параллелограмма; б) координаты его вершин и уравнения оставшихся двух сторон; в) длину и уравнение высоты, проведённой к большей стороне.

Решение. Шаг 1. Перепишем уравнение второй прямой в виде (2.1): 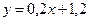. Поскольку угловые коэффициенты прямых различны (), то они не являются параллельными и, следовательно, содержат смежные стороны параллелограмма (например, 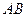и 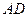). Шаг 2. Найдём координаты точки 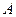из системы 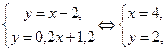то есть . Шаг 3. Найдём координаты точки 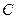с помощью формулы координат середины отрезка (в параллелограмме диагонали в точке пересечения делятся пополам): то есть 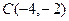. Шаг 4. Найдём уравнение прямой , как проходящей через точку 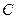параллельно прямой 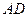: 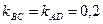, поэтому из уравнения (2.2) находим . Шаг 5. Найдём координаты точки 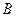как точку пересечения прямых 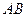и (самостоятельно) . Шаг 6. Найдём координаты точки 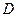с помощью формулы координат середины отрезка (самостоятельно) 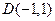. Шаг 7. Найдём уравнение прямой 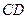, как проходящей через точк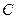и и 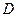(с помощью формулы (2.3)): . Шаг 8. Построим искомый параллелограмм. Шаг 9. Ответим на вопрос а), найдя 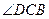. Поскольку и 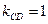, по формуле (2.6) получаем и . Шаг 10. Для ответа на вопрос в) необходимо найти длины сторон: и 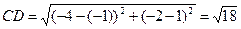. Таким образом будем искать длину и уравнение высоты , проведённой к стороне . По формуле (2.7) . Шаг 11. Уравнение прямой найдём по формуле (2.2) (она проходит через точку 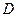перпендикулярно ). Поскольку 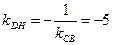(смотри следствие из теоремы 2.6), то .

Кривые второго порядка

Определение 2.3. Окружностью с центром в точке 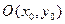и радиусом 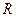называется геометрическое место точек координатной плоскости, удалённых от точки на расстояние .

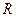Теорема 2.9. Уравнение окружности имеет вид . Доказать самостоятельно.

Пример 2.6. Найти центр и радиус окружности, заданной уравнением .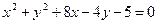

Решение. – Из данного уравнения вытекает, что центр окружности находится в точке , а радиус равен 5.

Определение 2.4. Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух заданных точек постоянна и больше расстояния между этими точками. Заданные точки называются фокусами, расстояние между ними – фокальным расстоянием.

Обозначим фокальное расстояние эллипса 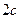, сумму расстояний от точки эллипса до фокусов - .

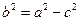Теорема 2.10. Уравнение эллипса имеет вид , где . Без доказательства.

Замечание. Величины 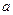и 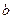называются большей и меньшей полуосями эллипса соответственно, точки с координатам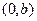и , , и 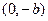– вершинами эллипса. Координаты фокусов равны 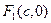и .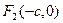

Пример 2.7. Построить эллипс, заданный уравнением .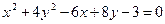

Решение.

.

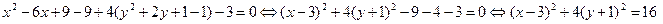Поделив последнее соотношение на 16, получим нормальное уравнение эллипса

,

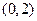из которого следует, что центр эллипса находится в точке , , . В новой системе координат вершины эллипса находятся в точках , , и 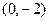, а фокусы – в точках 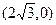и (поскольку ).

Определение 2.5. Гиперболой называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек постоянен и меньше расстояния между этими точками. Заданные точки называются фокусами, расстояние между ними – фокальным расстоянием.

Обозначим фокальное расстояние 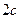, модуль разности расстояний от точки на гиперболе до фокусов – .

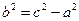Теорема 2.11. Уравнение гиперболы имеет вид , где . Без доказательства.

Замечание. Величины 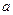и 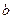называются действительной и мнимой полуосями гиперболы соответственно, точки с координатами и – вершинами гиперболы, точк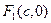и и 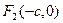– фокусами гиперболы, прямые 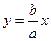и – асимптотами гиперболы.

Пример 2.8. Построить гиперболу, заданную уравнением .

Решение.

.

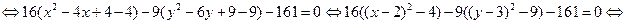
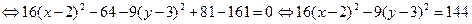Поделив последнее соотношение на 144, получим (после соответствующих преобразований) нормальное уравнение гиперболы

,

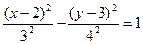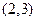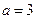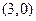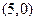из которого следует, что центр гиперболы находится в точке , , . В новой системе координат вершины гиперболы находятся в точках и , фокусы – в точках и 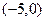(поскольку ), уравнения директрис имеют вид .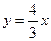

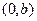Замечание. Если уравнение второго порядка после преобразования примет вид , то его графиком является сопряжённая гипербола, вершины которой находятся в точках с координатами и 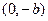, а фокусы – в точках с координатам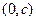и и .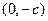

Определение 2.6. Параболой называется геометрическое место точек, равноудалённых от заданной точки (фокуса) и заданной прямой (директрисы), причём фокус не находится на директрисе. Расстояние от фокуса до директрисы называется фокальным параметром и обозначается .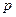

Теорема 2.12. Уравнение параболы имеет вид . Без доказательства.

Замечание. Точка с координатами 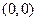называется вершиной параболы. Координаты фокуса равны 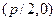, уравнение директрисы имеет вид: .

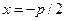Пример 2.9. Построить параболу, заданную уравнением .

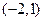Решение. . Из данного уравнения следует, что вершина параболы находится в точке , . В новой системе координат фокус находится в точке 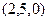, уравнение директрисы имеет вид .

Замечание. Если после преобразования уравнения второго порядка оно примет вид (1) 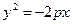, (2) , (3) 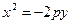, то его графиком будет парабола

После изучения уравнений эллипса, гиперболы и параболы естественным образом возникает вопрос: любое ли уравнение второго порядка определяет одну из данных кривых.

Рассмотрим общее уравнение второго порядка с двумя неизвестными:

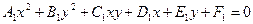. (2.11)

С помощью поворота системы координат на угол 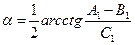уравнение (2.11) можно привести к виду

. (2.12)

Затем, применяя к уравнению (2.12) выделение полных квадратов и параллельный перенос системы координат, получим одно из следующих уравнений

, (2.13)

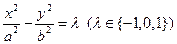, (2.14)

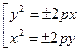, (2.15)

, (2.16)

причём переход от уравнения (2.12) к уравнению (2.13) возможен при , от (2.12) к (2.14) – при , от (2.12) к (2.15) или (2.16) – при .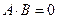

Уравнение (2.13) при определяет эллипс, при 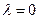– вырожденный эллипс, при 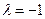– мнимый эллипс. Уравнение (2.14) при определяет гиперболу, при 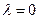– пару пересекающихся прямых, при 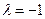– сопряжённую гиперболу. Уравнения (2.15) определяют параболы различных видов. Уравнения (2.16) при определяют пары параллельных прямых, а при 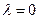– оси координат.

Дата добавления: 2014-01-11