Турбулентность и ее основные статистические характеристики Потери напора при турбулентном течении жидкости

Как было указано в п. 6.1, для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рис.6.4. Скорость беспорядочно колеблется около некоторого осредненного по времени значения υ _оср, которое в данном случае остается постоянным.

Характер линий тока в трубе в данный момент времени отличается большим разнообразием (рис.6.5).

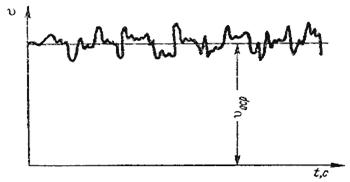
Рис. 6.4. Пульсация скорости в турбулентном потоке.

Рис. 6.5. Характер линий тока в турбулентном потоке

Турбулентные потоки рассчитывают по некоторым средним по времени расчетным параметрам течения, которые называют осредненными. Пульсационной добавкой скорости называют разность между истинной скоростью v в точке и осредненной скоростью 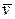. Для пульсационных добавок скорости имеем

.

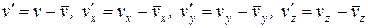Пульсационные добавки скорости имеют положительные и отрицательные значения и являются функциями времени и координат, причем эти функции являются случайными функциями. В ряде важных практических задач с достаточным приближением можно считать, что они подчиняются нормальному закону Гаусса о распределения вероятности.

Величины осредненной пульсационной добавки скорости, давления и напряжения всегда равны нулю. В качестве первой основной характеристики турбулентности, называемой интенсивностью турбулентности, принимают величину

.

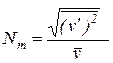Второй основной характеристикой турбулентности является линейная величина L, определяющая средний размер (в каком-либо направлении) области связанных между собой пульсаций скорости и называемая масштабом турбулентности. В прямоугольной системе координат масштаб L, например, по направлении оси oy выражается так:

,

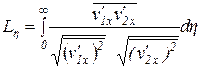где расстояние между точками 1 и 2 по оси оу или параллельной ей оси.

При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рис. 6.6. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.

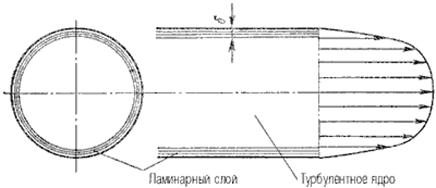
Рис. 6.6. Модель турбулентного режима движения жидкости

Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше формула, называемая формулой Вейсбаха-Дарси.

Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса Re и от безразмерного геометрического фактора - относительной шероховатости Δ/d (или Δ/r₀, где r₀ - радиус трубы).

Впервые наиболее исчерпывающей работы по определению λ были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости lg (1000λ) от lg Re для ряда значений Δ/r ₀. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на рис. 6.7. Прямая I соответствует ламинарному режиму движения жидкости.

Далее на графике можно рассматривать три области.

(6.17)

Первая область - область малых Re и Δ/r₀, где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re (отмечена на рис.6.7 прямой II). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(d/Δ_э) коэффициент λ определяется по полуэмпирической формуле Блазиуса

.

(6.18)

Для определения существует также эмпирическая формула П.К. Конакова, которая применима для гидравлически гладких труб

.

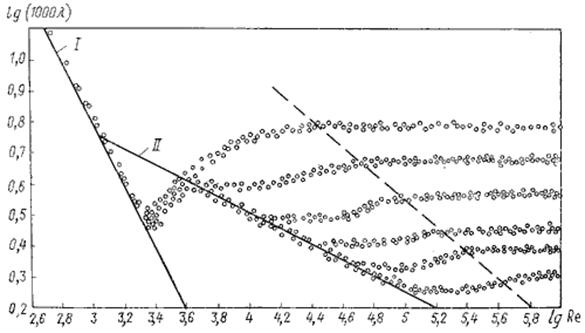Рис. 6.7. График Никурадзе

Во второй области, расположенной между линий II и пунктирной линией справа, коэффициент λ зависит одновременно от двух параметров - числа Re и относительной шероховатости Δ/r₀, которую можно заменить на Δ_э. Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:

(6.19)

,

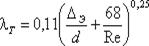где Δ_э - эквивалентная абсолютная шероховатость.

Характерные значения Δ_э (в мм) для труб из различных материалов приведены ниже:

Таблица 6.1

Эквивалентная шероховатость некоторых труб

Стекло
Трубы, тянутые из латуни, свинца, меди	0…0,002
Высококачественные бесшовные стальные трубы	0,06…0,2
Стальные трубы	0,1…0,5
Чугунные асфальтированные трубы	0,1…0,2
Чугунные трубы	0,2…1,0

Третья область - область больших Re и Δ/r₀, где коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.

Определение λ для этой области производят по упрощенной формуле Альтшуля:

(6.20)

,

(6.21)

или по формуле Прандтля – Никурадзе:

.

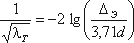Итак, потери напора, определяемые по формуле Вейсбаха-Дарси, можно определить, зная коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса и от эквивалентной абсолютной шероховатости Δ_э. Для удобства сводные данные по определению λ представлены в таблице 6.2.

Пользоваться приведенными в табл. 6.2 формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно воспользоваться номограммой Колбрука-Уайта (рис.6.8), при помощи которой по известным Re и Δ_э/ d весьма просто определяется λ.

Таблица 6.2

Формулы для определения коэффициента гидравлического трения

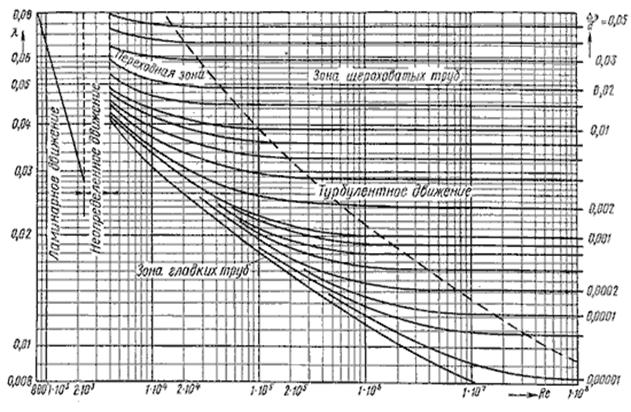
Рис. 6.8. Номограмма Колбрука-Уайта для определения коэффициента гидравлического трения

Дата добавления: 2014-01-11