Понятие функции комплексного переменного. Предел, непрерывность функции

С некоторыми функциями комплексного переменного мы уже встречались (см. §2 гл.1, ч.1). Дадим теперь общее определение функции комплексного переменного. Рассмотрим множество E комплексных чисел 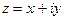, лежащих в комплексной плоскости (z), и множество G комплексных чисел лежащих в комплексной плоскости (w) (см. рис. 1).

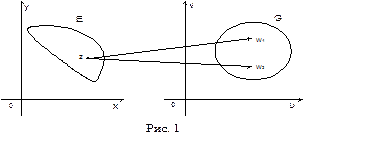
Определение 1. Если каждому комплексному числу 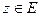поставлено в соответствие одно или несколько комплексных чисел множества G, то говорят, что на множестве задана однозначная или многозначная функция комплексного переменного. Пишут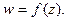

Множество E называют областью определения функции, а множество G - множеством значений функции.

Согласно определению 1 каждой паре действительных чисел поставлена в соответствие пара действительных чисел 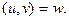Иными словами, на множестве E заданы две вещественные функци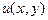и и двух вещественных переменных, т. е. одна функция комплексного переменного 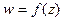эквивалентна двум вещественным функциям, при этом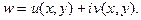

Приведем несколько примеров.

Дата добавления: 2014-01-11