
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Составление дифференциального уравнения колебаний
|
|
|
|
Эти методы получили наибольшее распространение. Ротационные приборы, позволяющие осуществлять измерения при более точном воспроизведении и однородности распределения скоростей сдвига, обладают известными преимуществами по сравнению с вышеперечисленными.
Приборы, в которых определение реологических характеристик осуществляетсяпутем вращения поверхностейв виде конус- конус,
конус- плоскость, сфера- сфера, кольцо- кольцо, диск- диск ( рис.1.2д ).
Ротационные вискозиметры подразделяются на приборы, в которых измерения выполняются при постоянном моменте, приложенном к одной из измерительных поверхностей, либо при постоянной скорости деформирования (вращения одной из измерительных поверхностей).
1.3. Виброреология
Развитие представлений об управлении свойствами дисперсных систем с помощью вибрационных воздействий связано с созданием раздела реологии дисперсных систем – виброреологии. В основе виброреологии лежит изучение закономерностей деформации и течения дисперсных систем при воздействии на них вибрации.
Специфическая особенность различных видов строительных материалов состоит в том, что вследствие сильно развитой поверхности раздела фаз поверхностные явления в таких гетерогенных системах приобретают решающее значение по сравнению с другими видами связей.
В науке и технике принято рассматривать механизм вибрационного воздействия на обрабатываемые среды в двух представлениях: корпускулярном и феноменологическом.
Корпускулярные базируются на представлении среды как гетерогенной (дискретной) системы и формулируются следующим образом. При вибрировании частицам среды сообщаются колебания, которые вызывают уменьшение внутреннего трения между ними. Уменьшение внутреннего трения происходит как за счет сообщаемой частицам различного градиента скорости, так и за счет того, что во время вибрирования, благодаря вводимой энергии, частицы ее раздвигаются.
Феноменологические рассматривают среду в виде гомогенной изотропной системы, физические свойства которой в рассматриваемом объеме одинаковы или меняются непрерывно. Гомогенные системы характеризуется вязкостью, плотностью, модулем упругости и другими физическими параметрами. Структура среды этими представлениями не рассматривается. Изучение свойств сред развивается в следующих направлениях:
- изучение закономерностей распространения колебаний (волновые процессы) с установлением радиуса действия вибраторов, коэффициентов затухания колебаний и других параметров;
- реологические исследования, устанавливающие зависимость вязкости системы от скорости сдвига, параметров вибрации и т.п..
Наиболее перспективными с позиций получения достоверных результатов при изучении деформации и течения исследуемых материалов и их реологических характеристик являются приборы, физические процессы в которых подобны реальным технологическим процессам. Так, например, при исследовании процессов смешивания целесообразнее использовать коаксиально- цилиндрические вискозиметры; для процессов заглаживания свежеуложенных бетонных смесей дисковыми рабочими органами - приборы, в которых определение реологических характеристик осуществляется путем вращения поверхностей в виде диск- диск; для процессов истечения (дозирования) – капиллярные вискозиметры и т.п..
(Замечание. Необходимо помнить, что влияние масштабного фактора и неоднородность материалов в процессе переработки оказывает существенное влияние на их реологические характеристики. Следовательно, реометрические исследования определяют качественные характеристики поведения материалов. Для получения достоверных результатов о влиянии вибрации на изменение свойств материалов необходимо, чтобы скорости сдвига были значительно ниже скорости вибрации, а их направления ортогональны (взаимноперпендикулярны)).
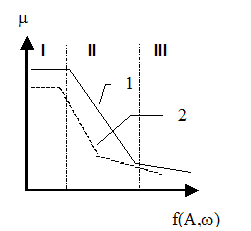
Типичная зависимость эффективной вязкости (вязкость в процессе вибрирования) рассматриваемых сред от параметров вибрации, представленная на рис.1.3 разделяется на три участка. Первый характеризует вязкость ненарушенной структуры, когда сочетание амплитуды и частоты колебаний не вызывает ощутимого уменьшения сил взаимодействия между частицами. Второй - ниспадающая кривая - указывает на то, что воздействие вибрации определенной интенсивности обеспечивает тиксотропное разрушение структуры смеси, связанное со значительным уменьшением эффективной вязкости. Третий участок асимптотически приближается к значению, равному вязкости предельно разрушенной структуры.
Наличие в перерабатываемых материалах поверхностно-активных веществ (ПАВ) позволяет уменьшить интенсивность вибраций в несколько раз, обеспечивая при этом полное разрушение их структуры, что способствует повышению долговечности вибрационных машин.
| Рис.1.3. Зависимость эффективной вязкости от сочетания параметров вибрации. 1.- без ПАВ. 2.- с добавками ПАВ. |
Влияние различных сочетаний амплитуды и частоты колебаний на эффективную вязкость оцениваются эмпирическими формулами типа 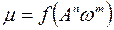 , где
, где 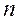 = 1, 2;
= 1, 2; 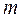 =1, 2, 3. Эти зависимости имеют недостаток: несоответствие размерности определяемого параметра, размерности правой части уравнения представляет определенные трудности распространению полученных зависимостей на подобные явления.
=1, 2, 3. Эти зависимости имеют недостаток: несоответствие размерности определяемого параметра, размерности правой части уравнения представляет определенные трудности распространению полученных зависимостей на подобные явления.
(Дополнение. Качественные и количественные связи различных процессов (явлений) целесообразнее устанавливать в виде обобщенных соотношений, полученных методами теории подобия и размерностей физических величин. Из гидродинамики известно, что подобие явлений течения в потоке жидкости обусловлено действием сил тяжести, инерции, внутреннего трения и характеризуется критериями Рейнольдса 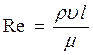 и Фруда
и Фруда 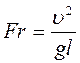 . Эти критерии включают основные независимые параметры: физические – коэффициент динамической (ньютоновской) вязкости
. Эти критерии включают основные независимые параметры: физические – коэффициент динамической (ньютоновской) вязкости 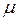 , плотность
, плотность 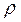 и ускорение
и ускорение 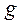 свободного падения; кинематические – скорость
свободного падения; кинематические – скорость 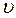 потока жидкости; геометрические – характерный размер
потока жидкости; геометрические – характерный размер 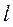 .
.
В качестве основных параметров, характеризующих процесс тиксотропного разрушения структуры смесей при вибрировании, необходимо считать: кинематические – амплитуду 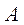 и частоту
и частоту  колебаний; геометрические – площадь
колебаний; геометрические – площадь 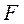 лобовой поверхности, передающей вибрацию; объем
лобовой поверхности, передающей вибрацию; объем  вибрируемой смеси.
вибрируемой смеси.
На основании вышеизложенных положений изменение эффективной вязкости смесей под действием вибрации можно описать уравнениями:
1.-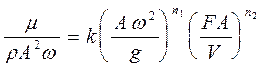 при значении
при значении 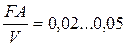 ;
;
2.-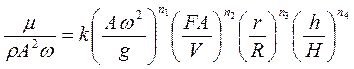 при значении
при значении 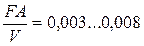 .
.
Здесь 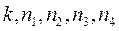 - коэффициенты, определяемые экспериментально;
- коэффициенты, определяемые экспериментально; 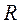 - радиус чаши в случае измерения вязкости одноцилиндровым ротационным вискозиметром (рис.1.5г);
- радиус чаши в случае измерения вязкости одноцилиндровым ротационным вискозиметром (рис.1.5г); 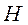 - толщина смеси;
- толщина смеси; 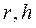 - координаты точки, в которой измеряется эффективная вязкость.
- координаты точки, в которой измеряется эффективная вязкость.
В уравнениях 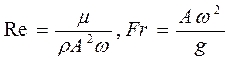 являются модифицированными критериями Рейнольдса и Фруда для процессов вибрирования смесей. Критерий-симплекс
являются модифицированными критериями Рейнольдса и Фруда для процессов вибрирования смесей. Критерий-симплекс 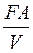 - характеризует эффективность геометрической формы поверхности вибратора. Чем больше его значение, тем выше коэффициент полезного действия вибромашины, определяемый как отношение количества энергии, потребляемой вибромашиной, к количеству энергии, поглощенной средой).
- характеризует эффективность геометрической формы поверхности вибратора. Чем больше его значение, тем выше коэффициент полезного действия вибромашины, определяемый как отношение количества энергии, потребляемой вибромашиной, к количеству энергии, поглощенной средой).
Разрушение структуры материала в вибромашиных достигается путем вибрации отдельных элементов или конструкции в целом. От амплитуды, частоты и траектории колебательного движения зависит структура смеси, интенсивность и характер перемешивания частиц материала, скорость направленного перемещения. В большинстве случаев в вибромашинах используют гармонические колебания.
В качестве примера рассмотрим плоскость, наклоненную к горизонту под углом 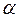 и совершающую прямолинейные колебания по гармоническому закону
и совершающую прямолинейные колебания по гармоническому закону 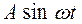 , где
, где 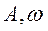 - соответственно амплитуда и частота колебаний плоскости. На частицу массой
- соответственно амплитуда и частота колебаний плоскости. На частицу массой 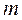 , лежащую на плоскости, действуют сила тяжести
, лежащую на плоскости, действуют сила тяжести 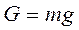 , нормальная реакция
, нормальная реакция 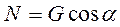 поверхности, сила трения
поверхности, сила трения 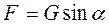 и сила инерции
и сила инерции 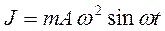 , направленная под углом
, направленная под углом 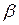 к плоскости (рис.1.7).
к плоскости (рис.1.7).
| Рис.1.7. Схема действия сил на частицу |
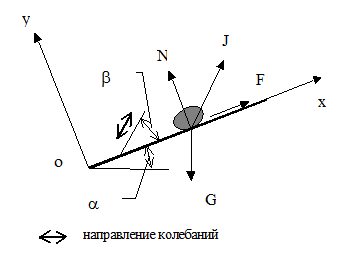
Движение частицы относительно вибрирующей поверхности в системе координат, связанной с этой поверхностью, описывается уравнениями: 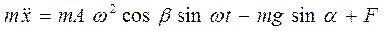
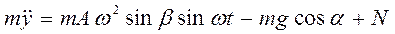
Если частица не отрывается от вибрирующей поверхности, то относительно этой поверхности ее ускорение 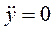 . Тогда из последнего уравнения находим
. Тогда из последнего уравнения находим 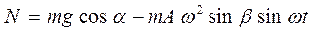
Условие отрыва частицы от вибрирующей поверхности выполняется при 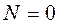 и имеет вид
и имеет вид 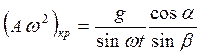 , где
, где 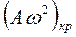 - критическое ускорение, при котором произойдет отрыв частицы от вибрирующей поверхности. Очевидно, что минимальное значение оно приобретает при
- критическое ускорение, при котором произойдет отрыв частицы от вибрирующей поверхности. Очевидно, что минимальное значение оно приобретает при 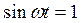 . Следовательно,
. Следовательно, 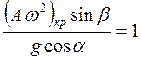 .
.
Естественно предположить, что поведение слоя материала, находящегося на вибрирующей поверхности, отличается от поведения отдельной частицы. Экспериментальными исследованиями установлено, что свойства слоя сыпучего материала при увеличении интенсивности вибрационного воздействия существенно изменяются. При безотрывных колебаниях материал находится в состоянии виброожижения, которое характеризуется уменьшением трения между частицами и относительным их перемещением, что способствует более плотной его упаковке. При наступлении отрыва материала от вибрирующей поверхности его состояние характеризуется виброкипением, при котором наблюдается увеличение объема материала за счет вовлечения воздуха и активное перемешивание частиц. В вязко-упруго-пластичных материалах при вибрировании также наблюдаются состояния виброожижения и виброкипения. При этом значение критического ускорения возрастает.
С учетом вышесказанного реальные значения ускорения колебаний вибрационных машин, используемые в различных технологических процессах, составляют: при перемещении материалов 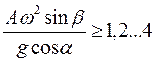 ; при уплотнении
; при уплотнении 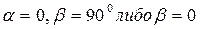 ,
, 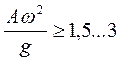 ; при перемешивании
; при перемешивании 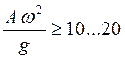 .
.
Иногда при инженерных расчетах вибрационных машин применяют понятие «эффективного коэффициента трения» 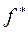 . Известно, что классический коэффициент сухого трения
. Известно, что классический коэффициент сухого трения 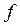 можно определить как отношение нижней границы силы
можно определить как отношение нижней границы силы 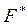 , приводящей тело в движение из состояния покоя, к нормальной реакции
, приводящей тело в движение из состояния покоя, к нормальной реакции 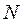 :
: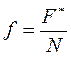 (закон Амонтона- Кулона). Необходимо отметить, что «эффективный коэффициент трения» ничего общего не имеет с коэффициентом сухого трения и свидетельствует лишь о том, что наибольшая сила трения
(закон Амонтона- Кулона). Необходимо отметить, что «эффективный коэффициент трения» ничего общего не имеет с коэффициентом сухого трения и свидетельствует лишь о том, что наибольшая сила трения 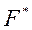 является суммой сил
является суммой сил 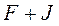 , т.е. выполняется условие
, т.е. выполняется условие 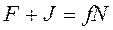 .
.
Раздел 2. Введение в теорию колебаний.
Создание современных машин немыслимо без учета колебательных процессов, во многом определяющих производительность машин, долговечность и надежность оборудования, качество продукции и условия труда оператора.
При проектировании вибрационных машин рекомендуются следующие этапы динамического расчета:
1) разработка динамической модели - идеализированное представление рассматриваемой системы, используемое при ее теоретическом исследовании и инженерных расчетах;
2) составление математической модели, соответствующей динамической модели рассматриваемого объекта, в виде дифференциальных, интегральных либо интегро-дифференциальных уравнений;
3) решение математической модели и анализ полученных результатов;
4) экспериментальная проверка, в результате которой определяется достоверность выбранной динамической модели.
Динамические модели условно разделяются на три вида: модели с распределенными параметрами, модели с сосредоточенными параметрами и комбинированные модели, состоящие из подсистем первых двух видов.
В моделях с распределенными параметрами наиболее полно отражаются свойства реальной механической системы. Однако из-за сложности решения подобных задач эти модели имеют весьма ограниченное применение. Они характеризуются бесконечным числом степеней свободы.
В инженерных расчетах наибольшее применение получили модели с сосредоточенными параметрами, в которых число степеней свободы ограничено. При построении таких моделей исходят из следующих предположений:
- инерционные свойства системы отображаются массами в случае поступательного движения, либо моментами инерции в случае вращательного движения, которые сосредоточены в отдельных точках или сечениях;
- эти точки или сечения соединены безынерционными упругодиссипативными, геометрическими и кинематическими связями.
2.1.Колебательные системы.
Процесс, характеризующийся многократным поочередным возрастанием и убыванием рабочего параметра во времени будем называть колебательным процессом или просто колебаниями.
Большинство наблюдаемых в природе и технике процессов являются колебательными: вибрация звучащей струны, землетрясения, распространение электромагнитных волн и т.п.
Ниже рассматриваются колебательные процессы, происходящие в механических системах, которые принято называть механическими колебаниями либо применяют термин вибрация.
Термин вибрация чаще всего применяют для процессов, характеризующихся малыми амплитудами колебаний и достаточно высокими частотами.
В качестве примера на рис. 2.1. изображены графики возможных механических колебаний

Классификация колебательных систем.
1. Число степеней свободы.
Количество независимых числовых параметров однозначно определяющих положение всех точек системы в пространстве. Различают системы с конечным и бесконечным числом степеней свободы. Если число степеней свободы несчетно, т.е. бесконечно, то в этом случае такие системы называют распределенными.
2. Линейные и нелинейные системы.
Система называется линейной, если ее свойства (упругость, масса, коэффициент трения) остаются постоянными при изменении состояния системы, т.е. не зависят от смещений, скоростей. Процессы в линейных системах описываются линейными дифференциальными уравнениями. Если это условие не соблюдается, то система нелинейная, а процессы описываются нелинейными дифференциальными уравнения
3. Стационарные и нестационарные системы.
Если свойства системы не изменяются на данном отрезке времени, то систему называют стационарной.
В противном случае, при изменении свойств системы во времени ее называют нестационарной. Процессы, происходящие в стационарных системах, описываются дифференциальными уравнениями с постоянными коэффициентами; нестационарные процессы - дифференциальными уравнениями с переменными коэффициентами.
4. Автономные и неавтономные системы.
Колебательные процессы в автономных системах происходят за счет внутренних источников энергии, либо энергии, сообщенной системе в виде начального возмущения. Остальные системы называются неавтономными.
5. Консервативные и неконсервативные системы.
Если полная механическая энергия системы остается постоянной при колебаниях, то система называется консервативной. В противном случае система неконсервативная. Среди неконсервативных систем можно выделить две системы, обладающие характерными свойствами.
Диссипативная система - система, в которой полная механическая энергия при любом движении соответствующей автономной системы убывает.
Систему называют автоколебательной, если она стационарна и автономна и если при определенных условиях в ней возможно самовозбуждение колебаний. Эти системы характеризуются наличием в них источника энергии не колебательной природы, причем поступление энергии регулируется движением самой системы.
Классификация колебательных процессов
1. Свободные колебания. Колебания, совершающиеся при отсутствии переменного внешнего воздействия и без поступления энергии извне, называются свободнымиколебаниями. Они происходят за счет первоначального накопления энергии системой. Свободные колебания происходят только в автономных системах.
2. Вынужденные колебания. Вызываются переменным внешним воздействием и характерны для неавтономных систем.
3. Параметрические колебания вызываются изменением во времени параметров самой системы и возникают в нестационарных системах.
4.Автоколебания (самовозбуждающиеся колебания).
Кинематические характеристики периодических колебаний.
Колебания называются периодическими, если любые значения колеблющейся величины повторяются через равные промежутки времени. На рис.2.2. представлен график периодических колебаний

Математическая запись периодических колебаний 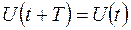 , где Т - период колебаний, с. Величина, обратная периоду колебаний называется частотой колебаний:
, где Т - период колебаний, с. Величина, обратная периоду колебаний называется частотой колебаний: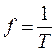 , [Гц]. В технике вводится понятие угловой частоты колебаний:
, [Гц]. В технике вводится понятие угловой частоты колебаний: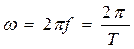 , [рад/с].
, [рад/с].
Простейшим и наиболее важным видом периодических колебаний являются гармонические колебания, переменная величина которых " U " (перемещение, скорость и т.п.) изменяется во времени по закону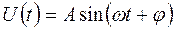 (2.1),где
(2.1),где 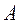 - амплитуда колебаний, наибольшее отклонение U(t);
- амплитуда колебаний, наибольшее отклонение U(t); 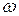 - угловая частота колебаний;
- угловая частота колебаний; 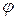 - начальная фаза колебаний.
- начальная фаза колебаний.
График гармонических колебаний представлен на рис. 2.3.
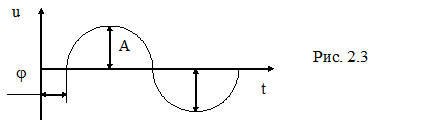
Аргумент (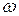 t +
t +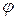 ) называется фазой колебаний в момент времени t.
) называется фазой колебаний в момент времени t.
Скорость гармонических колебаний 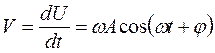 , а ускорение -
, а ускорение - 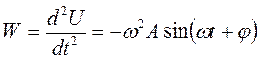 .
.
В технической литературе перемещение, скорость и ускорение при колебательном движении называют соответственно виброперемещение, виброскорость, виброускорение.
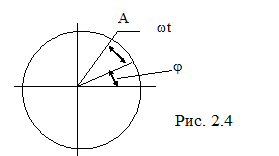
Для наглядного представления гармонических колебаний можно использовать круговую диаграмму (рис.2.4.).
Введем вектор длиной "А", который вращается с постоянной угловой скоростью. Начальное положение вектора задается углом 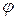 . Проекция вектора на вертикальную ось дает закон движения в форме (2.1). . Проекция вектора на вертикальную ось дает закон движения в форме (2.1).
|
Классификация сил.
Силы, действующие на механическую систему, разнообразны по своей природе и по роли, которую они оказывают на характер колебательного процесса. Рассмотрим основные из них.
Позиционные силы - силы, величина которых определяется отклонением системы от положения равновесия. К их числу относятся:
восстанавливающая сила упругости 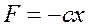 , где
, где 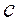 - коэффициент жесткости,
- коэффициент жесткости, 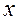 - перемещение (рис. 2.5а); при рассмотрении колебания плавающих конструкций выталкивающая сила Архимеда
- перемещение (рис. 2.5а); при рассмотрении колебания плавающих конструкций выталкивающая сила Архимеда 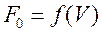 , где V - объем жидкости, вытесненный телом (рис. 2.5б); сила тяжести Q (рис. 2.5в); смешанные силы (рис. 2.5г)
, где V - объем жидкости, вытесненный телом (рис. 2.5б); сила тяжести Q (рис. 2.5в); смешанные силы (рис. 2.5г)
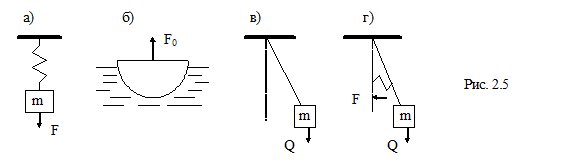
Восстанавливающие силы могут быть линейными (рис. 2.5а) и нелинейными, когда восстанавливающая сила не является линейной функцией перемещения системы от положения равновесия. Например, рис. 2.6 а, б.
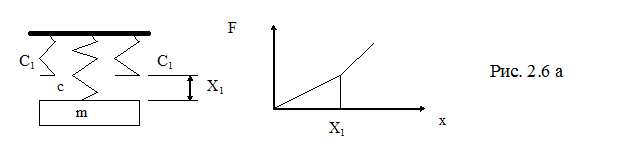
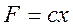 , где
, где 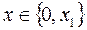 .
. 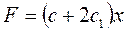 , где
, где 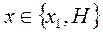
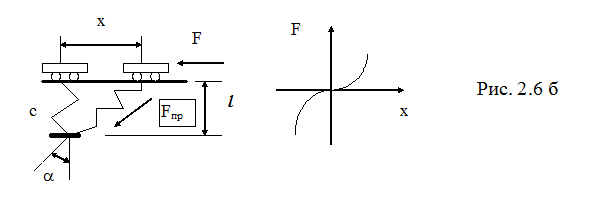
при 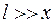 .
. 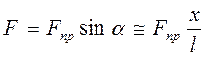 ;
; 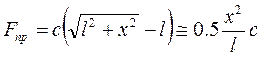 ;
; 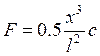 . (Известно, что
. (Известно, что 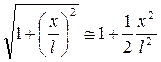 ).
).
Диссипативные силы - силы сопротивления пропорциональные скорости перемещения системы, приводящие к рассеиванию механической энергии при колебаниях. К их числу относятся, например. Сила сухого трения 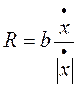 , где
, где 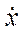 - скорость;
- скорость; 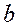 - положительная постоянная (рис. 2.7а). Сила вязкого трения
- положительная постоянная (рис. 2.7а). Сила вязкого трения 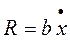 (рис. 2.7 б) и др..
(рис. 2.7 б) и др..
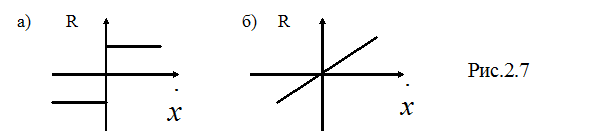
Диссипативные силы также могут быть нелинейными (рис. 2.7а).
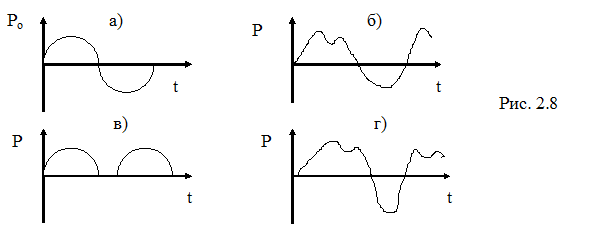
Вынуждающие силы - внешние силы, действующие на систему и вызывающие ее колебания. Они являются функциями времени и не зависят от движения системы, к которой приложены. К их числу относятся. Гармонические силы 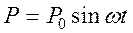 , возникающие, например, в результате вращения неуравновешенных масс (рис. 2.8а). Периодические силы негармонического характера
, возникающие, например, в результате вращения неуравновешенных масс (рис. 2.8а). Периодические силы негармонического характера 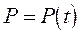 , например, инерционные нагрузки в кривошипно-шатунных механизмах (рис. 2.8б). Импульсные силы, возникающие в работе ударных устройств (рис. 2.8в). Нестационарные силы, действующие, например, на подвеску автомобиля во время его движения по неровностям дороги (рис. 2.8г).
, например, инерционные нагрузки в кривошипно-шатунных механизмах (рис. 2.8б). Импульсные силы, возникающие в работе ударных устройств (рис. 2.8в). Нестационарные силы, действующие, например, на подвеску автомобиля во время его движения по неровностям дороги (рис. 2.8г).
2.2. Системы с одной степенью свободы.
Механическая система обладает одной степенью свободы, если ее геометрическое положение в пространстве определяется одной координатой. Так, например, положение поршня в цилиндре определяется заданием расстояния от дна цилиндра; положение коленчатого вала - углом поворота и т.п.
Положим, что некоторая масса 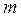 подвешена посредством пружины с коэффициентом упругости с и амортизатора с коэффициентом вязкого сопротивления
подвешена посредством пружины с коэффициентом упругости с и амортизатора с коэффициентом вязкого сопротивления 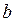 , как показано на рис. 2.9. Пусть переменная внешняя сила
, как показано на рис. 2.9. Пусть переменная внешняя сила 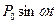 называемая вынуждающей силой и вызываемая каким-либо устройством, действует на массу
называемая вынуждающей силой и вызываемая каким-либо устройством, действует на массу 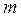 .
.
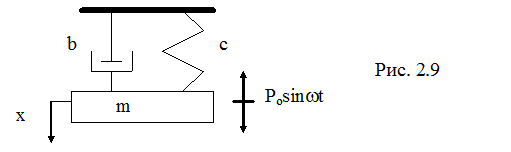
Задача состоит в том, чтобы определить закон движения массы m, вызванный вынуждающей силой, т.е. определить положение массы m в любой момент времени вдоль ординаты х.
При составлении уравнения динамики воспользуемся принципом ДôАламбера: - уравнения динамики механической системы формально совпадают с уравнениями равновесия этой системы, если к действующим внешним и внутренним силам, а также реакциям связей добавить фиктивные ( ДôАламбер овы) силы инерции.
Имеем 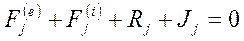 (2.2), где
(2.2), где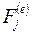 - внешние силы;
- внешние силы; 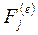 - внутренние силы;
- внутренние силы; 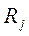 - реакции связей;
- реакции связей; 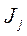 - силы инерции. В рассматриваемом случае имеем
- силы инерции. В рассматриваемом случае имеем
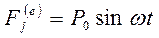 ;
; 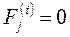 ;
; 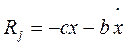 ;
; 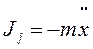 (2.3)
(2.3)
Подставив (2.3) в (2.2) и проведя группировку слагаемых, имеем
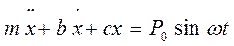 (2.4)
(2.4)
Полученное уравнение (2.4) принято называть дифференциальным уравнением движения системы с одной степенью свободы. Уравнение (2.4.) принято записывать в следующем виде. Разделим члены уравнения на 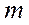 , получим
, получим 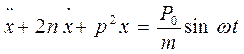 , где
, где 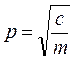 - угловая частота собственных колебаний, [рад/с];
- угловая частота собственных колебаний, [рад/с]; 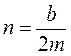 - коэффициент демпфирования.
- коэффициент демпфирования.
Замечание. При выводе уравнения (2.4) не принималось во внимание действие силы тяжести, т.к. отсчет ординаты 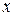 осуществлялся от положения равновесия. В этом положении сила тяжести
осуществлялся от положения равновесия. В этом положении сила тяжести 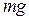 уравновешивается силой пружины
уравновешивается силой пружины 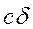 , где
, где 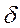 - статическое удлинение пружины под действием силы тяжести. С учетом силы тяжести уравнение (2.4) примет вид:
- статическое удлинение пружины под действием силы тяжести. С учетом силы тяжести уравнение (2.4) примет вид: 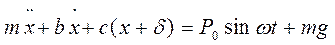 .
.
Рассмотрим второй способ составления дифференциального уравнения колебаний рассмотренной системы, который наиболее удобен в применении при рассмотрении систем с несколькими степенями свободы.
Воспользуемся уравнением Лангранжа: 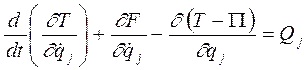 (а), где
(а), где 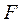 - диссипативная функция Релея;
- диссипативная функция Релея; 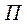 - потенциальная энергия;
- потенциальная энергия; 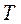 - кинетическая энергия системы; t - время;
- кинетическая энергия системы; t - время; 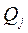 - обобщённая сила;
- обобщённая сила; 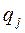 - обобщённая координата. Понятия обобщенных сил и обобщенных перемещений (координат) были предложены Релеем.
- обобщённая координата. Понятия обобщенных сил и обобщенных перемещений (координат) были предложены Релеем.
При малых перемещениях механических систем с голономными стационарными связями выражение функции Релея, потенциальной и кинетической энергий через обобщённые координаты 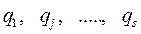 и обобщённые скорости
и обобщённые скорости 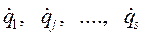 имеют вид:
имеют вид: 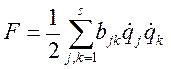 ,
, 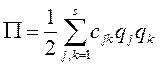 ,
, 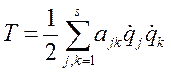 (б), где
(б), где 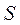 - число степеней свободы;
- число степеней свободы; 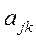 - инерциальные коэффициенты (в случае поступательного движения массы
- инерциальные коэффициенты (в случае поступательного движения массы 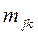 );
); 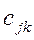 - коэффициенты жесткости;
- коэффициенты жесткости; 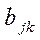 - коэффициенты вязкого сопротивления.
- коэффициенты вязкого сопротивления.
В механических системах связи являются голономными, т.е. геометрическими, если они налагают ограничения только на перемещения точек системы, но не на их скорости. Обобщенная сила - внешнее усилие (сила или момент). Обобщённые координаты – независимые между собой параметры любой размерности, число которых равно числу степеней свободы механической системы и которые однозначно определяют положение системы в пространстве.
С учетом (б) выражения для функции Релея, потенциальной и кинетической энергий имеют вид: 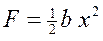 ,
, 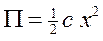 ,
, 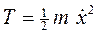 (в). Обобщенная сила
(в). Обобщенная сила 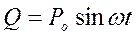 .
.
Найдём производные от выражений (2.7), необходимые для составления уравнений: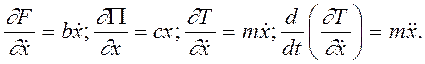
В соответствии с найденными выражениями дифференциальное уравнение колебаний примет вид: 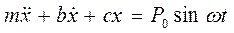 . (г)
. (г)
Очевидно, выражение (г) тождественно выражению (2.4).
При изучении изгибных колебаний балок и рамных конструкций применяют обратныйспособ составления уравнения движения системы, основанный на введении сил инерции приложенных к безмассному упругому “скелету ”. Во многих случаях приемлемой схемой балочных (рамных) конструкций служит упругая невесомая ось, с которой связано некоторое конечное число сосредоточенных масс.
Замечание. Естественным является описания упругого состояния балки с одной степенью свободы, представленной на рис.D, при помощи единичного главного удельного перемещения 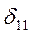 . Перемещение
. Перемещение 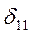 – перемещение в направлении “
– перемещение в направлении “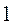 ”, вызываемое единичной силой
”, вызываемое единичной силой 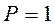 , действующей в направлении “
, действующей в направлении “ ”. Если в направлении “
”. Если в направлении “  ” действует сила
” действует сила 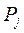 , то суммарное перемещение равно
, то суммарное перемещение равно 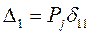 . Единичное перемещение при изгибе определяются по формуле Мора:
. Единичное перемещение при изгибе определяются по формуле Мора: 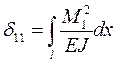 , где
, где 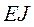 жёсткость геометрического сечения балки при изгибе;
жёсткость геометрического сечения балки при изгибе; 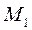 – изгибающий момент, вызванный единичной силой
– изгибающий момент, вызванный единичной силой 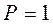 .
.
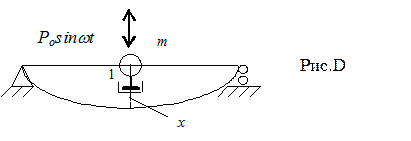
После введения некоторых понятий обратимся к составлению уравнений свободных колебаний системы.
Имеем невесомую балку на двух жёстких шарнирных опорах, несущую массу 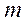 . Положим, что на массу
. Положим, что на массу 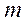 действует переменная сила
действует переменная сила 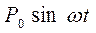 . Эта сила вызывает статическую деформацию в точке 1 расположения массы
. Эта сила вызывает статическую деформацию в точке 1 расположения массы 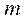 , величина которой равна
, величина которой равна 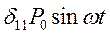 .
.
В точке, где размещена масса 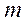 (точка 1), при колебаниях балки возникает ускорение
(точка 1), при колебаниях балки возникает ускорение 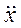 и соответствующая ему сила инерции
и соответствующая ему сила инерции 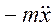 , вызывающая деформацию (перемещение)
, вызывающая деформацию (перемещение) 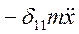 . Пусть диссипативная сила, действующая на массу
. Пусть диссипативная сила, действующая на массу 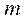 и равная
и равная 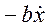 , возбуждает статическую деформацию
, возбуждает статическую деформацию 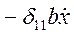 .
.
Прогиб 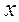 под действием этих сил в точке 1 равен:
под действием этих сил в точке 1 равен:
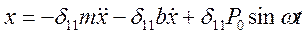 . (д)
. (д)
Уравнение (д) представляет собой дифференциальное уравнение вынужденных колебаний.
Определим размерность коэффициентов упругого и вязкого сопротивления, входящих в уравнение (2.4). Имеем 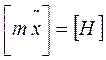 . Тогда
. Тогда 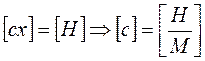 .
. 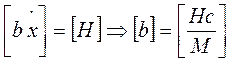 в отличие от коэффициента динамической вязкости
в отличие от коэффициента динамической вязкости 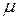 по Ньютону, имеющему размерность
по Ньютону, имеющему размерность 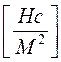 . Следовательно, коэффициент динамической вязкости
. Следовательно, коэффициент динамической вязкости 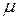 и коэффициент
и коэффициент 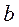 вязкого сопротивления имеют различный физический смысл.
вязкого сопротивления имеют различный физический смысл.
Рассмотрим частные случаи уравнения (2.4).
2.2.2. Свободные колебания без затухания. Пусть b =0 и 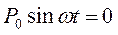 .
.
Уравнение (2.4) примет вид: 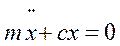 или
или 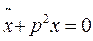 (2.5)
(2.5)
Положим, что масса 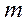 выведена из положения равновесия в положение
выведена из положения равновесия в положение 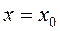 и отпущена c начальной скоростью. Для этого случая имеем начальные условия при t =0,
и отпущена c начальной скоростью. Для этого случая имеем начальные условия при t =0, 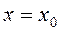 и
и 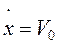 (2.6).
(2.6).
Решение уравнения (2.5) имеет вид 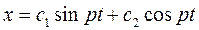 (2.7), где
(2.7), где 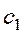 ,
,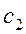 - произвольные постоянные. С учетом условия (2.6) получим
- произвольные постоянные. С учетом условия (2.6) получим 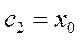 ;
; 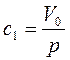 .
.
Поставив найденные значения произвольных постоянных в (2.7) получим выражение 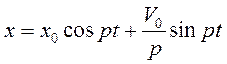 (2.8).
(2.8).
Выражение (2.8) представляет уравнение незатухающих свободных колебаний системы с одной степенью свободы при принятых начальных условиях.
Одно полное колебание совершается в течение такого промежутка времени, когда величина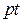 изменяется в пределах от 0 до
изменяется в пределах от 0 до 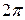 . Обозначая время одного колебания или период через T, имеем
. Обозначая время одного колебания или период через T, имеем 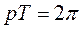 ,
, 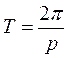 .
.
Очень часто уравнение (2.8) записывают в эквивалентной форме:
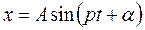 (2.9), где
(2.9), где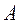 - амплитуда колебаний,
- амплитуда колебаний, 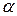 - начальная фаза.
- начальная фаза.
Найдем выражения для  и
и 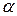 .
. 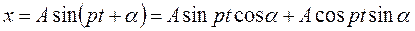
Очевидно для, тождественного равенства (2.8) и (2.9) необходимо, чтобы
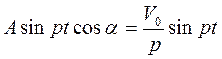 ,
, 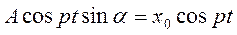
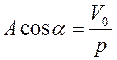 (2.10),
(2.10), 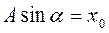 (2.11)
(2.11)
Разделив (2.11) на (2.10), получим 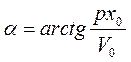 . Возводя в квадрат обе части равенств (2.10) и (2.11) и сложив, получим
. Возводя в квадрат обе части равенств (2.10) и (2.11) и сложив, получим 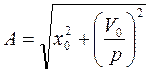 .
.
Если подвес груза образован несколькими упругими элементами (рис. 2.10а, б), то общий коэффициент жесткости определяется следующим образом.
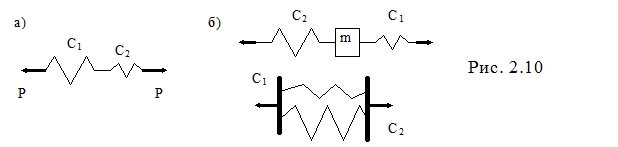
В случае последовательного соединения (рис. 2.10а) общая деформация системы 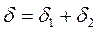 , где
, где 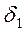 ,
,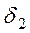 - соответствующая деформация упругого элемента.
- соответствующая деформация упругого элемента.
Так как 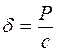 , где
, где 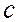 - общий коэффициент жесткости системы;
- общий коэффициент жесткости системы;
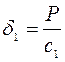 ,
,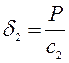 , имеем
, имеем 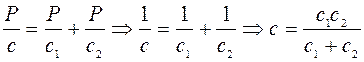 .
.
В случае параллельного соединения (рис. 2.10б) имеем
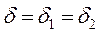 ;
; 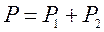 ,где
,где 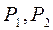 , - соответствующее усилие, воспринимаемое каждым упругим элементом
, - соответствующее усилие, воспринимаемое каждым упругим элементом 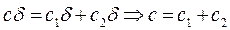 .
.
Пример. Определить жесткость и собственную частоту колебания системы, представленной на рис. 2.11. Система представлена массой М, размещенной на консольной балке. Причем М >>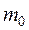 , где
, где 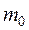 - распределенная масса балки. В подобных случаях считают балку, как упругую невесомую конструкцию, обладающую определенной жесткостью
- распределенная масса балки. В подобных случаях считают балку, как упругую невесомую конструкцию, обладающую определенной жесткостью
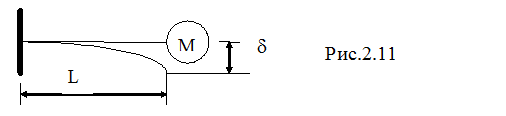
Имеем 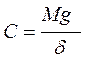 ;
; 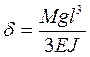 , где EJ - жесткость балки. Тогда
, где EJ - жесткость балки. Тогда 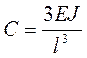
Собственная частота колебаний по определению равна: 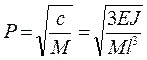
В заключении рассмотрим, какую работу совершает сила упругости 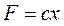 при свободных гармонических колебаниях за один период. Известно, что работа, совершаемая силой на малом перемещении
при свободных гармонических колебаниях за один период. Известно, что работа, совершаемая силой на малом перемещении 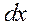 равна
равна 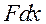 , либо
, либо 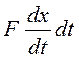 .
. 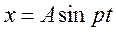 . За время полного колебания фаза
. За время полного колебания фаза 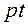 изменится от 0 до
изменится от 0 до 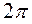 и, следовательно, время t изменится от 0 до
и, следовательно, время t изменится от 0 до 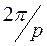 .
.
Работа W силы упругости F за время полного колебания равна:
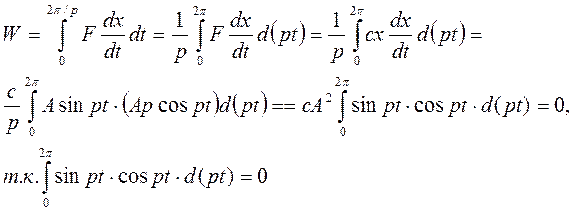
Вывод. Если работа сил упругости за время полного колебания равна нулю, то в процессе колебаний сумма потенциальной и кинетической энергии системы остается неизменной и, следовательно, рассматриваемая идеализированная модель после выведения ее из положения равновесия будет совершать колебания без затухания. По данной выше классификации колебательных систем рассматриваемая система – консервативная и автономная. Анализ идеализированных моделей в виде консервативных и автономных систем позволяет определить важную для практики характеристику исследуемого объекта – собственную частоту колебаний.
2.2.3. Свободные колебания с затуханием.
Пусть 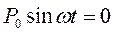 . Реально в технических устройствах возникают свободные колебания с затуханием, описываемые уравнением
. Реально в технических устройствах возникают свободные колебания с затуханием, описываемые уравнением 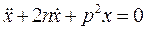 (2.12),
(2.12), 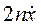 - член, определяющий силу затухания. Для решения уравнения (2.12) составим характеристическое уравнение
- член, определяющий силу затухания. Для решения уравнения (2.12) составим характеристическое уравнение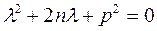 (2.13), корнями которого служит величина
(2.13), корнями которого служит величина 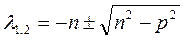
Очевидно, что значения 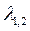 могут быть действительными либо комплексными.
могут быть действительными либо комплексными.
Рассмотрим характерный в практике проектирования вибрационного оборудования случай, когда n < р. Корни уравнения (2.13) комплексные и представятся в виде: 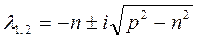 . Примем начальные условия в виде: при
. Примем начальные условия в виде: при 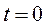 ,
, 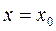 ,
, 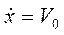 . Общее решение имеет вид
. Общее решение имеет вид 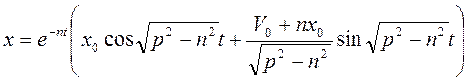 , либо в эквивалентной форме
, либо в эквивалентной форме 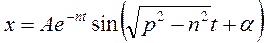 , где
, где 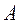 - амплитуда колебаний,
- амплитуда колебаний, 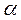 - начальная фаза
- начальная фаза 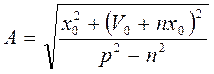 ,
, 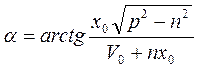 .
.
Решение представляет собой произведение двух функций экспоненты и синусоиды. Кривая колебаний представлена на
рис. 2.12.
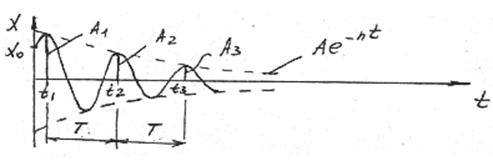 Рис.2.12 Рис.2.12
|
Величину 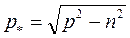 - называют собственной частотой свободных затухающих колебаний и обычно она мало отличается от собственной частоты системы без демпфирования (уравнение (2.5)). Период колебаний
- называют собственной частотой свободных затухающих колебаний и обычно она мало отличается от собственной частоты системы без демпфирования (уравнение (2.5)). Период колебаний 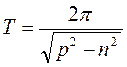 .
.
Величины последовательных отклонений, соответствующих моментам времени 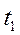 ,
, 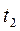 ,
, 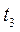 , когда
, когда 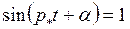 равны:
равны: 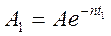 ;
;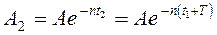 ;
;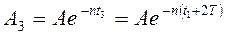 . Можно видеть, что
. Можно видеть, что 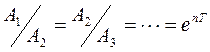 - есть постоянная величина. Следовательно, последовательность пиковых значений образует геометрическую прогрессию и
- есть постоянная величина. Следовательно, последовательность пиковых значений образует геометрическую прогрессию и 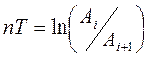 .
.
Величину 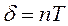 называют логарифмическим декрементом. Она часто используется как характеристика диссипативных свойств колебательной системы. Иногда для характеристики затухания используют величину
называют логарифмическим декрементом. Она часто используется как характеристика диссипативных свойств колебательной системы. Иногда для характеристики затухания используют величину 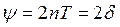 , называемую коэффициентом поглощения.
, называемую коэффициентом поглощения.
Конкретные значения коэффициента поглощения определяются материалом и конструктивными особенностями устройства.
Так, например, в расчетах строительных конструкций для стали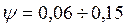 ; для железобетона
; для железобетона 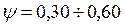 .
.
Пример. При изучении колебаний железобетонной конструкции установлено, что коэффициент поглощения 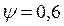 . Найти изменение собственной частоты колебаний конструкции при наличии затухания.
. Найти изменение собственной частоты колебаний конструкции при наличии затухания.
Имеем 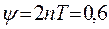 , откуда
, откуда 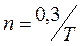 .
. 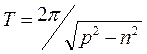 , тогда
, тогда 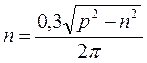 (2.14).
(2.14).
Решая (2.14), получим 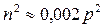 . Таким образом, собственная частота колебаний системы, равная
. Таким образом, собственная частота колебаний системы, равная 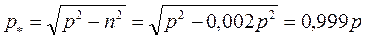 отличается от частоты соответствующих незатухающих колебаний на 0,1 %.
отличается от частоты соответствующих незатухающих колебаний на 0,1 %.
Вывод. При определении собственной частоты колебаний исследуемой системы диссипативные свойства системы не учитываются.
Теперь рассмотрим, какую работу совершает сила вязкого сопротивления 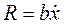 за один период гармонических колебаний
за один период гармонических колебаний 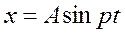 . Имеем:
. Имеем:
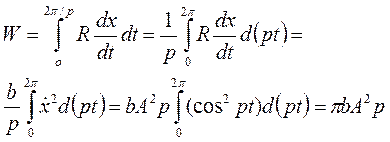
Эта работа изображается площадью заштрихованной на рис. 2.13 гистерезисной петли, имеющей форму эллипса.

Таким образом, при вязком трении относительный гистерезис прямо пропорционален частоте колебаний.
Пример. Определить коэффициент демпфирования гидравлического демпфера системы, представленной на рис. 2.14.
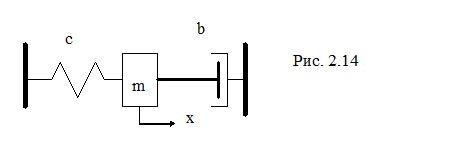
Гидравлический демпфер представляет закрытый цилиндр с поршнем, который имеет отверстия для протекания жидкости из одной полости в другую.
Пусть 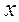 перемещение массы
перемещение массы 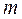 жестко связанной с поршнем за время t. Секундный объемный расход Q жидкости из одной полости в другую в результате перемещения поршня равен
жестко связанной с поршнем за время t. Секундный объемный расход Q жидкости из одной полости в другую в результате перемещения поршня равен 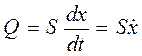 (2.15), где S - площадь поршня.
(2.15), где S - площадь поршня.
С другой стороны секундный объемный расход q жидкости по трубе определяется по формуле Пуазейля: 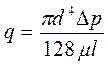 (2.16), где l,d соответственно длина и внутренний диаметр трубы, причем l>>d - коэффициент динамической вязкости (по Ньютону);
(2.16), где l,d соответственно длина и внутренний диаметр трубы, причем l>>d - коэффициент динамической вязкости (по Ньютону); 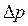 - перепад давлений в полостях цилиндра.
- перепад давлений в полостях цилиндра.
Обозначим через Z число пропускных отверстии, тогда Q=qZ. С учетом (2.15) выражение (2.16) имеет вид: 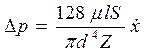 (2.17). Сила R, действующая на поршень, равна с учетом (2.17)
(2.17). Сила R, действующая на поршень, равна с учетом (2.17) 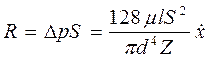 (2.18). Ранее сила вязкого сопротивления определялась как
(2.18). Ранее сила вязкого сопротивления определялась как 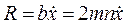 (2.19). Подставив (2.18) в (2.19), с учетом
(2.19). Подставив (2.18) в (2.19), с учетом 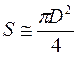 , где D - диаметр поршня (отверстиями пренебрегаем), получим
, где D - диаметр поршня (отверстиями пренебрегаем), получим 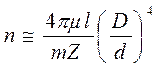 (2.20). Из формулы (2.20) вытекает, что основное влияние на коэффициент демпфирования n оказывает отношение диаметров поршня и отверстия. Выбирая параметры поршня и жидкость, которая заполняет цилиндр, можно получить затухающее колебательное движение (n<p).
(2.20). Из формулы (2.20) вытекает, что основное влияние на коэффициент демпфирования n оказывает отношение диаметров поршня и отверстия. Выбирая параметры поршня и жидкость, которая заполняет цилиндр, можно получить затухающее колебательное движение (n<p).
2.2.4. Вынужденные колебания без затухания.
Предположим, что наряду с восстанавливающей силой F=cx на тело действует вынуждающая сила, изменяющаяся по гармоническому закону. Тогда 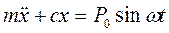 ;
; 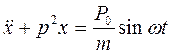 (2.21)
(2.21)
Как известно, общее решение уравнения (2.21) является суммой решения однородного уравнения (2.5) и частного решения и запишется в виде 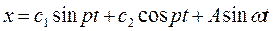 . Правая часть полученного решения представляет результат наложения свободных колебании на колебания, происходящие с частотой
. Правая часть полученного решения представляет результат наложения свободных колебании на колебания, происходящие с частотой  вынуждающей силы.
вынуждающей силы.
Величину 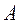 найдем из уравнения (2.21) путем подстановки частного решения
найдем из уравнения (2.21) путем подстановки частного решения 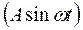 :
: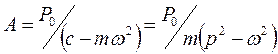 (2.22). Постоянные
(2.22). Постоянные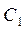 и
и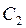 определим из нулевых начальных условий: при t =0, x =0,
определим из нулевых начальных условий: при t =0, x =0, 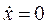 .
.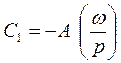 ;
; 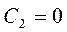 . Тогда общее решение имеет вид:
. Тогда общее решение имеет вид: 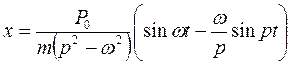 (2.23).
(2.23).
Выражение 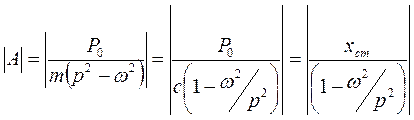 - амплитуда вынужденных колебаний, где
- амплитуда вынужденных колебаний, где 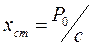 перемещение, соответствующее случаю статического приложения силы Р0 .
перемещение, соответствующее случаю статического приложения силы Р0 .
Характер колебаний имеет вид (рис. 2.15) если 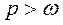
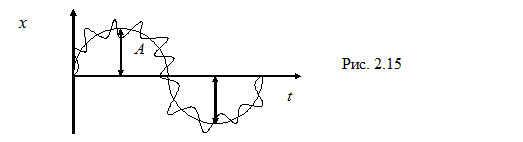
Выражение 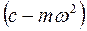 называют динамической жесткостью системы.
называют динамической жесткостью системы.
Динамичность действия вынуждающей силы характеризуют отношением
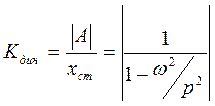 (2.24) и называют коэффициентом динамичности либо коэффициентом усиления. Зависимость коэффициента динамичности от соотношения
(2.24) и называют коэффициентом динамичности либо коэффициентом усиления. Зависимость коэффициента динамичности от соотношения 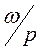 представлена на рис. 2.16 называется амплитудно-частотной характеристикой.
представлена на рис. 2.16 называется амплитудно-частотной характеристикой.

Вынужденные колебания системы описываются уравнением
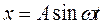 (2.25). Если
(2.25). Если 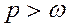 , то A >0 в соответствии с выражением (2.24) и согласно (2.25) вынужденные колебания по фазе совпадают с частотой возбуждающей силы. Если
, то A >0 в соответствии с выражением (2.24) и согласно (2.25) вынужденные колебания по фазе совпадают с частотой возбуждающей силы. Если 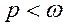 , то A <0, из формулы (2.25) получим
, то A <0, из формулы (2.25) получим 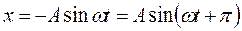 , что означает сдвиг по фазе на величину
, что означает сдвиг по фазе на величину 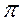 перемещения системы относительно возбуждающей силы. Обратим на это обстоятельство особое внимание, так как в системах виброизоляции, рассмотренных ниже, оно имеет большое значение. При
перемещения системы относительно возбуждающей силы. Обратим на это обстоятельство особое внимание, так как в системах виброизоляции, рассмотренных ниже, оно имеет большое значение. При 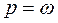
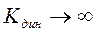 .
.
2.2.5. Вынужденные колебания с затуханием.
В реальных системах всегда присутствуют диссипативные силы. Уравнение колебаний при наличии силы затухания пропорциональной скорости примет вид:
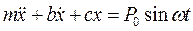 ,
, 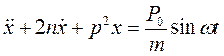 (2.26)
(2.26)
Общее решение (2.26) имеет вид: 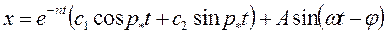 ,
,
где 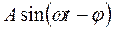 - частное решение уравнения;
- частное решение уравнения; 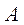 - амплитуда вынужденных колебаний;
- амплитуда вынужденных колебаний; 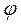 - угол сдвига фаз между направлением возбуждающей силы и перемещением.
- угол сдвига фаз между направлением возбуждающей силы и перемещением.
Можно отыскивать постоянные 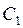 ,
, 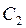 ,
, 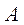 и
и 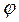 известными математическими способами. Тем не менее при нахождения решения пойдем иным путем, чтобы лучше понять явление с физической точки зрения. Известно, что искомое решение представляет собой вынужденные колебания по закону синуса и перемещение точки определяется уравнением
известными математическими способами. Тем не менее при нахождения решения пойдем иным путем, чтобы лучше понять явление с физической точки зрения. Известно, что искомое решение представляет собой вынужденные колебания по закону синуса и перемещение точки определяется уравнением 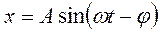 , где
, где 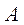 и
и 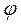 пока неизвестные постоянные величины. Тогда все силы (четыре слагаемых уравнения 2.26) также должны изменяться по закону синуса с частотой
пока неизвестные постоянные величины. Тогда все силы (четыре слагаемых уравнения 2.26) также должны изменяться по закону синуса с частотой 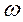 .
.
Представим эти силы векторами на векторной диаграмме (рис. 2.17), причем дифференцирование в этом случае эквивалентно умножению длины вектора на 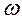 с одновременным поворотом его на прямой угол в сторону вращения.
с одновременным поворотом его на прямой угол в сторону вращения.
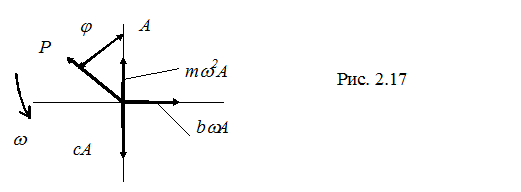
Рассмотрим подробнее построение диаграммы. Отложим амплитуду перемещения  вертикально вверх. Амплитуда восстанавливающей силы равна
вертикально вверх. Амплитуда восстанавливающей силы равна 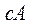 и направлена в противоположную сторону (вертикально вниз). Амплитуда силы затухания равна
и направлена в противоположную сторону (вертикально вниз). Амплитуда силы затухания равна 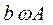 и повернута по отношению к восстанавливающей силе на 90° в сторону вращения. Амплитуда силы инерции равна
и повернута по отношению к восстанавливающей силе на 90° в сторону вращения. Амплитуда силы инерции равна 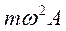 и повернута по отношению к силе затухания также на 90°. Возбуждающая сила P0 расположена под углом
и повернута по отношению к силе затухания также на 90°. Возбуждающая сила P0 расположена под углом 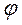 к перемещению А. Согласно закону Ньютона рассматриваемые силы, действующие на систему, должны находиться в равновесии:
к перемещению А. Согласно закону Ньютона рассматриваемые силы, действующие на систему, должны находиться в равновесии:
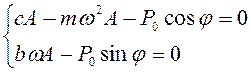 . Найдем выражения для неизвестных
. Найдем выражения для неизвестных 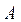 и
и 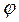 , решая систему уравнений следующим образом. Перенесем слагаемые включающие Р 0 в правую часть. Возведем обе части уравнений в квадрат и сложим. Найдем выражение для
, решая систему уравнений следующим образом. Перенесем слагаемые включающие Р 0 в правую часть. Возведем обе части уравнений в квадрат и сложим. Найдем выражение для  . Поделим второе уравнение на первое найдем
. Поделим второе уравнение на первое найдем 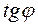 и
и 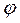 . (Предлагается проделать эти действия самостоятельно). В результате получим:
. (Предлагается проделать эти действия самостоятельно). В результате получим: 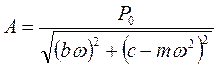 ,
, 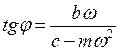 (2.27). Тогда вынужденные установившиеся колебания системы будут иметь вид:
(2.27). Тогда вынужденные установившиеся колебания системы будут иметь вид:
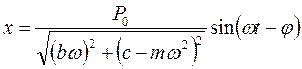 (2.28). Подставим в (2.27)
(2.28). Подставим в (2.27) 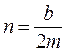 ,
,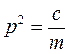 ,
,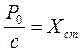 получим
получим 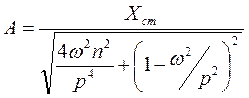 ,
,