Узагальнимо модель, яка введена в темі 2

Модель

Тема 7.

Глосарій

Резерв чистої премії	Net premium reserve
Чиста ризикова величина	Net amount at risk
Премія збережень	Savings premium
Ризикова премія	Risk premium
Чисте збереження	Pure savings
Контракт чистого дожиття	Pure endowment
Премія ризику виживання	Survival risk premium
Чиста річна премія	Net annual premium
Формула різниці премій	Premium difference formula
Середнє зважене	Weighted average
Теорема Хаттендорфа	Hattendorff's theorem
Універсальний (гнучкий) контракт страхування життя	Universal (flexible) life insurance policy
Технічний прибуток	Technical gain
Прибуток інвестицій	Investment gain
Прибуток смертності	Mortality gain
Диференціальне рівняння Тіле	Thiele's differential equation
Сила процента	Force of interest

Контрольні запитання для самоперевірки:

1. Що таке резерв чистої премії?

2. Наведіть приклад обчислення резерву чистої премії?

3. Що таке чиста ризикова величина?

4. Дайте визначення поняттю «премія збережень»?

5. Що таке ризикова премія?

6. Як визначається премія ризику виживання?

7. Як обчислюється резерв чистої премії за безтерміновим контрактом страхування життя?

8. За якими формулами обчислюється резерви чистої премії в проміжні моменти?

9. Охарактеризуйте зміст поняття «перетворення контракту».

10. Що таке технічний прибуток і як його визначити?

Тема 7. Декременти

План

7.1. Модель

7.2. Сила декременту

7.3. Вкорочений час життя

7.4. Загальна форма контракту страхування

7.5. Резерв чистої премії

7.6. Неперервна модель

7.7. Глосарій

Припустимо, що особа знаходиться в певному стані (статусі) у віці 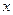. Людина покидає цей статус в момент 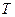з однієї з 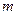попарно виключених причин (вони пронумеровані від 1 до 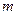). Ми будемо вивчати пару випадкових величин: час майбутнього життя в певному статусі 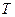і причину декремента .

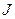В класичній ситуації, при страхуванні непрацездатності, початковий статус є "Активний" і можливі причини декремента – це "Непрацездатність" і "Смерть".

При іншому підході 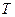- час життя, що залишився, для (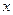), є з розділенням двох причин декремента, а саме смерть через "Нещасний випадок" і з "Іншої причини". Ця модель підходить для страхування з подвійною сумою страхування у випадку випадкової смерті.

Спільний розподіл імовірності для 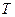і 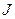можна записати в термінах функцій щільності 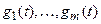таких, що

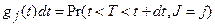(1.1)

є ймовірність декремента з причини 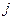протягом нескінченно малого інтервалу часу (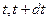). Очевидно,

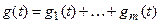. (1.2)

Якщо декремент виникає в момент 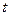, умовна ймовірність того, що причиною декремента є 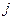дорівнює

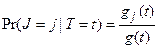. (1.3)

Введемо символ

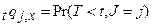(1.4)

або більш загально

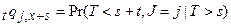. (1.5)

Остання ймовірність обчислюється за формулою

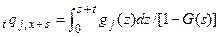. (1.6)

Дата добавления: 2014-01-11