Построение начального опорного плана

Рассмотрим закрытую транспортную задачу. Являясь задачей линейного программирования, транспортная задача может быть решена симплексным методом. Однако специфическая форма системы ограничений данной задачи позволяет существенно упростить обычный симплексный метод. Модификация симплексного метода применительно к транспортной задаче называется распределительным методом. По аналогии с общим случаем решение в нем осуществляется по шагам, и каждому шагу соответствует разбиение переменных на основные (базисные) и свободные.

Прежде чем исследовать методы нахождения опорного решения транспортной задачи, рассмотрим теорему о ранге матрицы из коэффициентов при неизвестных системы ее ограничений.

Теорема: Ранг матрицы из коэффициентов при неизвестных системы ограничений транспортной задачи равен т+п -1, где т и п - количество поставщиков и потребителей соответственно.

Следствие: Решение закрытой транспортной задачи должно содержать т+п -1 базисных переменных (где т – число поставщиков, п – число потребителей) и mn- (m+n- 1) небазисных, равных нулю переменных.

Каждому разбиению переменных 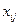задачи на базисные и свободные соответствует базисное решение и, как следствие, заполнение таблицы поставок, которое также назовем базисным. Иными словами, распределение поставок называется базисным, если переменные, соответствующие заполненным клеткам, можно принять за базисные переменные. Клетки, отвечающие базисным переменным, будем называть базисными или заполненными или загруженными (т.к. мы используем исключительно базисные распределения поставок), а клетки, соответствующие свободным переменным, - свободными или пустыми.

Подобно тому, как это было в симплексном методе, в распределительном методе решения транспортной задачи будем переходить от одного базисного распределения поставок к другому в сторону невозрастания целевой функции вплоть до оптимального решения. Для начала такого движения потребуется исходное базисное распределение поставок – так называемый опорный план.

Если в опорном решении транспортной задачи число отличных от нуля не­известных равно т+п -1, то решение называется невырожденным, а если их меньше, то вырожденным.

Специальная табличная структура транспортной модели для построения начального опорного плана позволяет применить следующие методы:

1) метод северо-западного угла (диагональный метод);

2) метод минимального элемента (метод наименьшей стоимости);

3) метод Фогеля.

Дата добавления: 2014-01-11