Уравнение движения

Применим к жидкости, протекающей через объем V, закон количества движения. Для твердого тела он может быть сформулирован следующим образом: скорость изменения количества движения тела 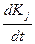равна силе F_j, действующей на тело, т.е.

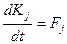. (4.9)

В этом уравнении количество движения K_j=mu_j, m – масса тела, u_j – скорость центра массы тела.

Для жидкости в контрольном объеме уравнение (4.9) можно записать исходя из следующих соображений. Количество движения жидкости, приходящееся на единицу объема, равно ru_j, следовательно, скорость изменения количества движения жидкости в контрольном объеме, состоящая из локальной и конвективной составляющих, будет равна:

. (4.10)

Теперь выразим силу F_j, вызывающую изменение количества движения жидкости в контрольном объеме, через параметры, характеризующие течение жидкости. Как известно, на жидкость в контрольном объеме действуют распределенные поверхностные и массовые силы – поверхностные и массовые напряжения. Поверхностные напряжения обязаны своим происхождением воздействию среды, окружающей выделенный объем V. Роль такой среды может играть твердая стенка или просто окружающая жидкость. Величину поверхностной силы dP_j, действующей на элементарную площадку n_idS, вычисляют как произведение dP_j=s_ijn_idS,

в котором s_ij – поверхностное напряжение, действующее на площадку dS с нормалью i в направлении оси j. Расчленим поверхностное напряжение s_ij на два слагаемых с помощью символа Кронекера d_ij, одно из которых не зависит от вязкости жидкости, давление p, а другое зависит от нее, это вязкие напряжения t_ij, нормальные и касательные. Получаем: s_ij=-pd_ij+t_ij.

Поверхностная сила, действующая на контрольный объем, тогда будет равна интегралу:

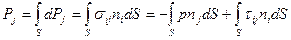. (4.11)

(Пояснение. Индекс j появился следующим образом. При вычислении интеграла 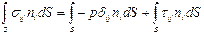символ Кронекера не равен нулю только при i=j).

Массовыми силами, действующими на каждую жидкую частицу, являются силы, не зависящие от наличия соседних частиц или от действия окружающей среды. Примером массовой силы является сила тяжести, пропорциональная массе. Обозначим массовое напряжение вектором f_j, тогда массовая сила, действующая на единицу объема, будет равна rf_j, а массовая сила, действующая на объем V, вычисляется как интеграл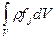. Подставляя ее, а также выражения (4.11) и (4.10) в уравнение (4.9) получаем интегральную форму уравнения движения в напряжениях:

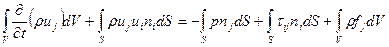. (4.12)

Здесь, как и в предыдущем случае, поверхностные интегралы могут быть преобразованы в объемные с помощью теоремы Остроградского – Гаусса, после чего, используя основную лемму механики сплошной среды, получим дифференциальную форму уравнения движения в напряжениях:

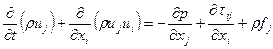. (4.13)

Левая часть уравнения (4.13) представляет собой соответственно нестационарную и конвективную скорости изменения количества движения в единице объема, три члена в правой части уравнения представляют собой силу давления, силу вязкости и массовую силу, приходящуюся на единичный объем жидкости.

Если продифференцировать произведения в левой части уравнения (4.13) и использовать уравнение неразрывности (4.5), то можно получить еще одну форму уравнения движения в напряжениях, в котором все члены отнесены к единице массы жидкости:

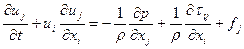. (4.14)

В случае невязкой жидкости уравнения движения (4.14) принимают тот вид, который называют уравнениями Л. Эйлера:

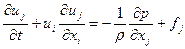. (4.15)

Контрольные вопросы

1. Пояснить, почему интеграл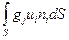представляет собой разность потоков свойства g_j жидкости (массы, количества движения), протекающей через контрольную поверхность.

2. Дать определение массового расхода жидкости.

3. Дать определение объемного расхода жидкости.

4. При каком движении жидкости будет происходить накопление (убывание) ее в контрольном объеме?

5. Записать уравнение неразрывности в дифференциальной форме с точки зрения неподвижного наблюдателя.

6. Записать уравнение неразрывности в дифференциальной форме с точки зрения наблюдателя, движущегося вместе жидкостью вдоль линии тока.

7. Получить уравнения движения в форме (4.14).

8. Получить дифференциальную форму уравнений движения (4.13).

Дата добавления: 2014-01-11