Круглая затопленная струя

ЛЕКЦИЯ 16

Рассмотрим затопленную струю. Затопленной называют струю, которая распространяется в покоящейся среде.

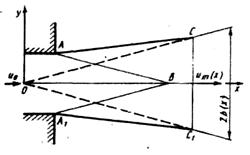Рис.6.6. Схема затопленной струи

Пусть из сопла с прямым срезом выходит поток с постоянной по сечению скоростью и0. На начальном участке струи образуются из-за турбулентного обмена количеством движения с окружающей средой турбулентные зоны смешения CAB и С1А1В (рис. 6.6). Внутри тре-

угольника АВА ₁, включая его границы, поток имеет скорость и₀. На линиях АС и А ₁ С ₁ скорость и = 0 (расположение системы координат показано на рисунке). На линиях АВ и А ₁ В и линиях АС и А ₁ С ₁ вертикальная составляющая скорости v = 0. Струя захватывает и ускоряет подсасываемую жидкость турбулентными пульсациями, но сама замедляется, так как при постоянном давлении вдоль струи суммарное количество движения постоянно.

Участок, в котором скорость по оси струи равна u ₀, называют начальным. Ниже по течению за начальным участком скорость начнет уменьшаться также и по оси струи. До сечения СС ₁ этот участок называют переходным. Далее течение в струе будет таким, как будто оно вызвано источником в точке О (рис. 6.6). За сечением СС ₁ расположен участок струи, который называют основным. На всем протяжении струя вовлекает в движение окружающую неподвижную жидкость, расширяется и подтормаживается.

Такая схема струи с гладкими границами является идеализированной (подобная идеализация полезна при создании расчетных методов).

Уменьшение скоростей в струе происходит иначе, чем при движении воздуха в диффузоре, когда через все поперечные сечения протекает одно и то же его количество. Струя же все время захватывает все новые и новые количества относительно спокойного окружающего воздуха.

Если струя распространяется в среде воздуха, имеющего температуру или концентрацию иные, чем в начальной массе струи, то вследствие перемешивания происходит постепенное изменение температур или концентраций в струе.

Изменение скоростей в струе вызывается обменом между турбулентными молями (частицами) основной массы струи с частицами окружающего воздуха. Обменом этих же частиц обусловливается изменение температур и концентраций, поэтому изменение их (температур и концентраций) должно находиться в соответствии с изменением скоростей.

Как показывают эксперименты, статическое давление в струе остается постоянным и почти точно равным статическому давлению в окружающем воздухе.

Вследствие равенства статических давлений (в струе и в окружающем воздухе) в соответствии уравнением движения в полных импульсах (5.3), количество движения Gu воздуха остается неизменным вдоль всей струи G ₀ u ₀ = G ₁ u ₁ = const и, следовательно, во сколько раз уменьшается средняя скорость u, во столько же раз увеличивается массовый расход воздуха G в сечении струи.

При изучении струй (изменений, происходящих вдоль струи, скоростей, расходов, температур, концентраций) пользуются не абсолютными величинами, а относительными - безразмерными. Так, например, линейные размеры (расстояния от выходного отверстия струи, ширину струи и др.) измеряют в долях какого-либо характерного размера, для круглой трубы - в долях диаметра трубы, для прямоугольной - в долях короткой стороны; скорости выражают в долях начальной скорости истечения, а изменение скоростей в каком-либо сечении - в долях осевой скорости в этом сечении и т. д.

Такой способ обработки экспериментальных данных в безразмерных - отно-сительных - величинах позволяет результаты единичного эксперимента распро-странять на целый класс подобных явлений.

Установлено, что струи, вытекающие из геометрически подобных патруб-ков (с геометрическим подобием всех элементов, формирующих струю), имеют одни и те же относительные величины независимо от абсолютных величин диаметра, начальной скорости и т. д.

На формирование и структуру струи, а следовательно, и на все закономер-ности ее решающее влияние оказывает степень турбулентности, определяющая интенсивность переноса и перемешивания частиц при истечении.

Степень турбулентности струи обусловливается, главным образом, формой подводящего участка трубы перед отверстием (соплом, конфузором) и формой самого отверстия, из которого вытекает струя.

Наличие в выходном сечении трубы неравномерного поля скоростей, которое может получиться вследствие, например, близости поворота или может быть вызвано искусственными мерами - вставкой в трубу разного рода «завих-рителей», вызывает турбулизацию струи.

Наиболее теоретически изученными являются струи, вытекающие из круглого отверстия и прямоугольной бесконечного протяжения щели. Полученные таким путем зависимости приведены в табл. 1 и достаточно удовлетворительно согласуются с опытными данными. Относительные величины скоростей, расходов и пр. даны в таблицах в зависимости от величины, характеризующей интенсивность перемешивания: коэфициента турбулентности струи а. Численные значения величины a определяются экспериментальным путем и приведены в табл.2.

B соответствии с теорией принципиальная схема струи представляется в следующем виде (рис.6.7, а). Границы струи прямолинейны и при своем продолжении пересекаются на некотором расстоянии внутри трубы, в точке 0, называемой полюсом струи. Можно представить себе, что в полюсе помещен точечный источник и из него распространяются лучи, граница которых обус-ловлена кромками трубы. Как следует из схемы, положение полюса относительно кромок трубы определяет угол расширения струи. Чем больше угол расширения струи, тем интенсивнее перемешивание и тем больше численное значение коэфициента турбулентности а и тем ближе полюс струи к кромкам трубы.

Численные значения коэфициентов турбулентности струи а определяют экспериментальным путем.

Таблица 1

В этих выражениях индекс х — относится к сечению, расположенному на расстоянии x от сопла, 0 —к сечению на выходе из сопла, окр — к окружающеку воздуху, в котором распространяется струя.

Распределения скоростей в выходных отверстиях Таблица 2

	для круглого отверстия, поджатого на выходе (конфузора) а = 0,066 … 0,07
	для трубы без поджатия а = 0,07 … 0,08
	для трубы, снабженной коротким диффузором, а = 0,08
	для короткого отрезка трубы с осевым венти-лятором в ней а ≈ 0,2
v 0 – скорость на оси струи; c 0 – средняя скорость в отверстии

В практических расчетах для круглой струи значение a принимается обычно равным 0,08. Центральный угол конуса границы струи составляет ≈ 30,5˚.

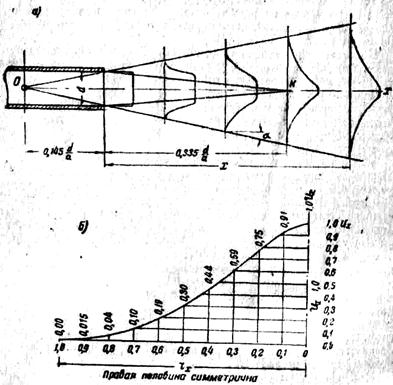
Рис. 6.7. Свободная круглая струя

Кроме границ внешнего конуса, в котором движется вся масса струи, на рис. 6.7, а показаны еще границы внутреннего обращенного конуса (начало его у кромок трубы и конец в точке К. В границах, образованных внутренним конусом скорости, температуры и концентрации остаются неизменными и такими же, как в отверстии трубы. От границ внутреннего конуса до внешнего простирается пограничный слой; скорости в нем постепенно уменьшаются до нуля на границах струи.

На рис. 6.7, б приводится половина профиля круглой струи на основном участке. За единицу принята осевая скорость. За единицу принята осевая скорость. В безразмерных координатах профиль скорости является универсальным и описывается уравнением Шлихтинга

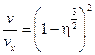, (6.1)

где η = y/r_x – безразмерная радиальная координата точки струи;

y – радиальная координата точки струи;

r_x – радиус внешней границы струи

Построение круглой свободной струи производится следующим образом.

1. Проводим прямую, изображающую геометрическую ось трубы; она же будет и аэродинамической осью струи. Наносим кромки выходного сечения трубы.

2. Находим полюс струи. Он лежит на оси внутри трубы, от выходной кромки ее на относительном расстоянии .

Из полюса через кромки трубы проводим лучи внешней границы струи (тангенс угла расширения внешней границы):

tgα = 3,4 а.

3. Отыскиваем конец начального участка (переходное сечение), для чего от кромки трубы откладываем .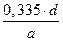

Радиус переходного сечения равен 3,3 r (r - радиус отверстия трубы).

Соединяя центр переходного сечения с кромками отверстия трубы, получаем границы ядра.

Тангенс угла сужения границ ядра равен:

tg α₁ = 1,5 а.

Радиус r_x струи на заданном расстоянии х от отверстия трубы:

r_х = r + 3,4 а х.

4. График распределения скоростей в поперечном сечении струи можно построить, пользуясь безразмерным профилем скоростей в основном участке струи (рис. 6.7, б).

Остальные закономерности круглой струи приводятся в табл.1.

Дата добавления: 2014-01-11