Часть 2

Автоматика, автоматизация и автоматизирование системы управления технологическими процессами».

Курс лекций по дисциплине

End Sub

Loop

End If

End Sub

Loop

End Sub

Do

End Sub

Loop

End Sub

Do

End Sub

Loop

MsgBox "Выполнено " & count & " итераций цикла."

В процедуре ChkLast инструкции внутри цикла выполняются только один раз до того как условие примет значение False.

Пример:

Sub ChkLast()

count = 0

Num = 9

Num = Num - 1

count = count + 1

Loop While Num > 10

MsgBox "В цикле выполнено " & counter & " итераций."

Имеется два способа проверки условия в конструкции Do...Loop с помощью ключевого слова Until:

· условие проверяется до входа в цикл (процедура Sub ChkFirstUntil())

· условие проверяется после хотя бы однократного выполнения цикла (Процедура Sub ChkLastUntil())

Пример:

Sub ChkFirstUntil()

count = 0

Num = 20

Do Until Num = 10

Num = myNum - 1

count = count + 1

MsgBox "В цикле выполнено " & counter & " итераций."

Пример:

Sub ChkLastUntil()

count = 0

Num = 1

Num = Num + 1

count = count + 1

Loop Until Num = 10

MsgBox "В цикле выполнено " & counter & " итераций."

Инструкции Do...Loop можно завершить с помощью инструкции Exit Do. Например, для завершения бесконечного цикла используется инструкция Exit Do If...Then...Else. Если условие имеет значение False, цикл будет выполняться как обычно.

В следующем примере переменной Num присваивается значение, приводящее к бесконечному циклу. В блоке If...Then...Else проверяется условие Num, а затем завершается выполнение инструкции Do...Loop, таким образом предотвращая бесконечный цикл.

Пример:

Sub ExitExample()

count = 0

Num = 9

Do Until Num = 10

Num = myNum - 1

count = count + 1

If Num < 10 Then Exit Do

MsgBox "В цикле выполнено " & count & " итераций."

Примечание. Для прекращения бесконечного цикла используются клавиши ESC или CTRL+BREAK.

В приведенном ниже примере показано, как можно использовать инструкции Do...Loop. Внутренний цикл Do...Loop выполняется 10 раз, затем логической переменной присваивается значение False, после чего он преждевременно завершается с помощью инструкции Exit Do. Внешний цикл завершается немедленно после проверки значения логической переменной.

Пример:

Sub Test()

Dim Check, Count

Check = True: Count = 0 ' Инициализирует переменные.

Do ' Внешний цикл.

Do While Count < 20 ' Внутренний цикл.

Count = Count + 1 ' Увеличивает счетчик.

If Count = 10 Then ' Если условие истинно.

Check = False ' Присваивает переменной значение False.

Exit Do ' Завершает внутренний цикл.

Loop Until Check = False ' Немедленно завершает внешний цикл.

Лектор: к.т.н. Червинский Вячеслав Леонидович.

Математический аппарат исследования систем автоматического управления

§ Математическое представление сигналов

Сигналы являются информацией обуславливающей функционирование систем автоматического управления. Они делятся на регулярные (детерминированные), а так же могут быть случайные сигналы. Регулярным называется сигнал, математического представления, который, является заранее заданной функцией времени. К основным типам регулярных сигналов относится периодические, почти периодические и непериодические сигналы. Периодические сигналы, представляющие функции времени, которые записываются в виде f(t)=f(T+t).

Почти периодические сигналы являются функцией времени. Представляются суммой гармонических составляющих с произвольными частотами. Могут получаться в результате сложения двух синусоид с некратными частотами.

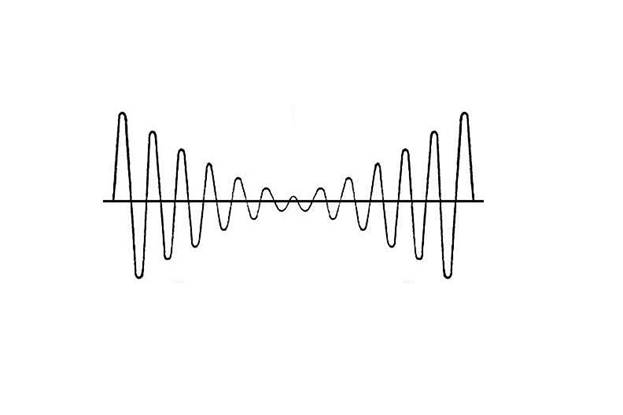
Непериодические сигналы, которые задаются функцией времени в пределах конечного (в интервале t₁ ≤ t ≤ t₂) или же полубесконечного t₁ ≤ t ≤ ∞ интервала времени вне которых она тождественно равна 0.

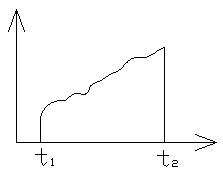
Случайный, это такой сигнал, который не может быть описан заранее заданной функцией времени.

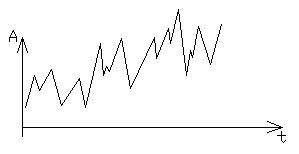
Для математического представления случайных сигналов используют методы теории вероятности и математической статистики. По технике управления применяются непрерывные и дискретные сигналы. Непрерывные сигналы представляют непрерывную функцию времени, в некоторых случаях эта функция может иметь разрывы первого или второго рода, приобретают при этом некоторые конечные или же бесконечные сигналы.

Дискретные сигналы могут быть дискретные по уровню и по времени. Для исследования динамических свойств САУ используются типовые сигналы, к которым относятся ступенчатый, импульсный, гармонический, линейно-возрастающий и т.д.

Ступенчатый сигнал:

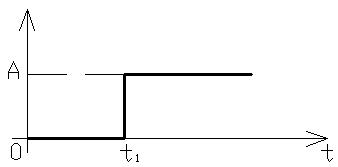
x(t)=A*f(t)

Существует единичная ступенчатая функция, которая показывает, что момент времени ступенчатый сигнал – это один из наиболее простых видов сигнала используется при расчетах переходных процессов. Он представляет функцию времени которая в момент времени

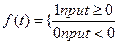
2) Импульсный сигнал. Его можно рассматривать как предел прямоугольного импульса высотой h и длительностью ∆t. При h -> ∞ и ∆t -> 0 при этом площадь этого импульса A=h*∆t.

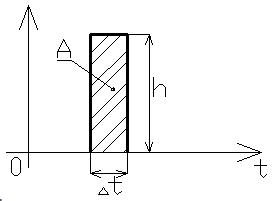
3) Гармонический синусоидальный и косинусоидальный. Широко используется для исследования частотных свойств, элементов и систем автоматического управления. Они представляют собой функцию вида: x(t)=A*sin(ωt+φ)

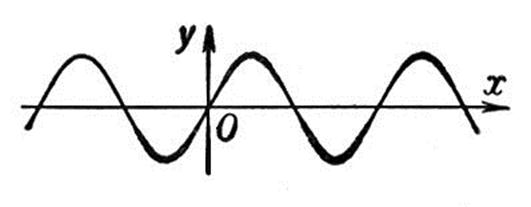
4) Линейно-возрастающий сигнал используется для исследования динамики следящихся систем.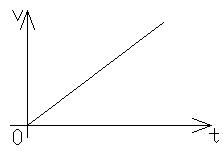

ТЕМА: Понятие о статических и динамических характеристик САУ

Оценка качества функционирования САУ базируется на исследовании их статической и динамической характеристик.

Статической называются характеристики отображающие связь между входными воздействиями и выходными координатными в стационарном (установившемся) режиме. Для систем с одним входом и одним выходом существует одна статическая характеристика, представляющая собой зависимость выходной величины от входной в стационарном режиме вида: x_уст=β*U_уст

β – коэффициент усиления

x_уст­ – входная величина; U_уст – выходная для линейных систем β=const, а для нелинейных β=f(U)

Системы с несколькими входами характеризуются семействами статических характеристик. Каждое такое семейство представляет зависимость выходной величины от входной.

Динамическими называются характеристики, отображающие переходной процесс в системе при различных формах воздействий. Они могут быть получены на базе передаточных систем.

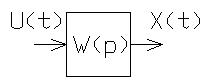
Передаточной функцией называется отношение операторных изображений по Лапласу, выходной и входной величин при нулевых начальных условиях, слева от нуля. Если же система имеет один вход, то ее передаточная функция определяется по формуле:

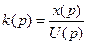
Где: x(p) и U(p) – изображение превращений выходной и входной величин при нулевых начальных условиях.

В общем виде передаточная функция является правильной рациональной дробью следующего вида:

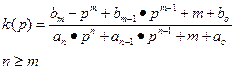
a_i и b_i – коэффициенты которые выражаются через параметры систем.

Нули и полюса передаточной функции, корни характеристического уравнения могут быть либо вещественными, либо комплексно-сопряженными. Если же в качестве входного воздействия используется единичная ступенчатая функция, то получается переходной процесс, который представляет собой переходную функцию. Эта функция является зависимостью выходной величины от времени и в общем случае записывается выражением:

h(t)=X_в(t)+X_св(t)

X(t) – вынужденная составляющая которая при единичном ступенчатом воздействии равна коэффициенту усиления системы.

X_св(t) – свободная составляющая которая характеризует процесс перехода систем в новое состояние. В устойчивой системе X_св(t) с течением времени -> 0. Если же входное воздействие представляет единичную импульсную функцию, то получаемый при этом процесс называется импульсной переходной функцией.

Импульсная переходная функция является производной от переходной функции.

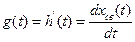
При оценке динамических свойств системы, широкое распространение получили частотные характеристики. Они характеризуют реакцию системы на гармонические воздействия следующего вида:

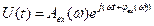
При изменении ω от нуля до ∞.

Частотные характеристики обычно используются для исследования устойчивости систем. А так же для построения переходного процесса САУ.

Амплитудно-фазовая частотная характеристика (АФЧХ) представляет собой отношение комплексных выражений вида:

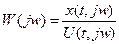
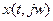- выходной сигнал

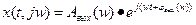
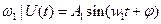
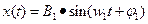
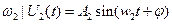
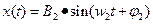
В теории автоматического управления так же пользуются логарифмическими частотными характеристиками (ЛЧХ). Они широко применяются для определения структуры и параметров регуляторов, которая формирует заданный закон переходного процесса систем автоматического управления.

Характеристический вектор системы при изменении ω от нуля до ∞, описывает своим концом на комплексной плоскости кривую, которая называется годографом.

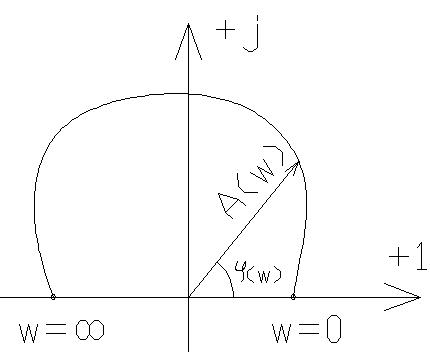
ТЕМА: Типовые звенья и структурные схемы автоматического регулирования.

При приложении к системе возмущающих или же задающих воздействии, ее стационарное состояние соответствует новому значению нагрузки или же задание устанавливается не сразу, а по прошествии некоторого времени определяется переходным процессом. Характер переходного процесса в любой системе автоматического регулирования зависит от динамических свойств элементов из которых состоит эта система.

В зависимости от области применения САР эти элементы могут быть самыми разнообразными и иметь различное конструктивное исполнение, принципы устройства работы и т.д. Они могут выполняться в виде машин операторов, приборов и устройств различного принципиального действия (механического, электрического, пневматического, гидравлического и т.д.). Однако, все эти элементы независимы от назначения и конструкции исполнения. Могут быть подразделены на ограниченное число звеньев, обладающих одинаковыми динамическими свойствами, такие звенья называются типовыми динамическими звеньями. Т.е. типовые звенья могут отличаться друг от друга характером протекаемых в них переходных процессов, различные по своему назначению и конструкции исполнения элементы САР могут описываться одинаковыми дифференциальными уравнениями.

Типовые динамические звенья делятся на следующие группы:

1. Безинерционное звено (усилительное)

2. Инерционное звено первого порядка, апериодическое звено первого порядка

3. Колебательное звено

4. Дифференциальное звено

5. Интегрирующее звено

6. Звено транспортного запаздывания

Будем считать, что все типовые динамические звенья являются звеньями направленного действия, т.е. они имеют один вход и один выход и лишены внутренних обратных связей.

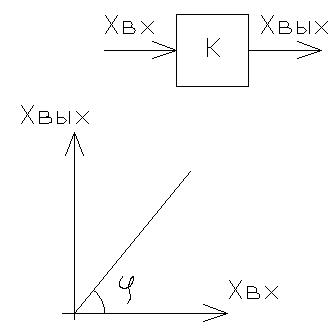
1. Безинерционное звено (усилительное).

Называется такое звено, в котором в каждый момент времени существует пропорциональность между входной и выходной величинами, которое записывается формулами:

x_вых=k*x_вх

R – Коэффициент пропорциональности, который так же называется коэффициентом усиления звена.

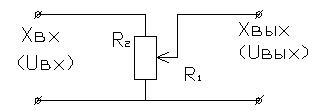
Примером безинерционного звена может служить реостатический датчик, в котором выходное напряжение определяется соотношением между сопротивлением реостата и участка реостата.

2. Инерционное звено 1-го порядка.

Оно описывается следующим уравнением:

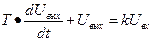
Т – постоянная времени звена

К – коэффициент усиления звена

Пример:

Дифференциальное уравнение нарастания температуры в термокамере

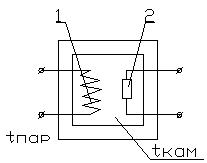
1-нагреватель

2-датчик температуры

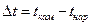
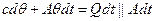
С – теплоемкость термокамеры

Θ – превышение температуры воздуха в камере над температурой нагреваемого воздуха

А – теплопередача нагревательного элемента, т.е. это энергия, которая отдается нагревательным элементам в термокамеру за 1 секунду и поднимает температуру на 1⁰С

Q – мощность нагрева от нагревательного элемента

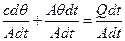
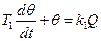
Т­₁=С/А; к₁=1/А

Т₁ – постоянная времени термокамеры

К₁ – коэффциент теплопередачи термокамеры, (с*град)/кал

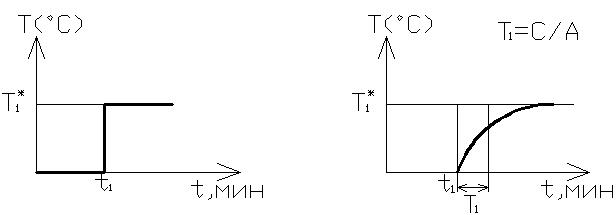
Передаточная функция апериодического звена 1-го порядка записывается в следующем виде:

W(p)=k₁/Т_{1 p+1}

P – оператор Лапласа

3. Колебательное звено

Типовое колебательное звено описывается дифференциальным уравнением 2-го порядка. При этом колебательное звено образуется при наличии двух ёмкостей, одна из которых способна запасать потенциальную энергию, а вторая кинетическую энергию. При приложении к такому звену внешнего воздействия, запас энергии ёмкостей может периодически меняться и сопровождаться переходом потенциальной энергии в энергию кинетическую, но из-за того, что с течением времени запас энергии в С/С уменьшается за счет теплового рассеяния энергии (в следствии электрического сопротивления и т.д.), то это приводит к затуханию колебаний и таким образом к устойчивому состоянию работы устройства.

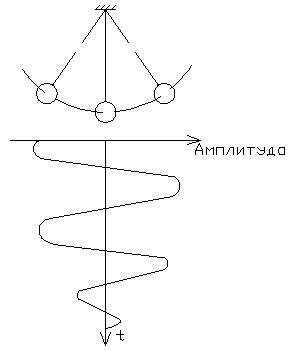
Но так же возможен и другой процесс. В случае, если запас энергии в С/С повышается, то А колебаний с течением времени будет расти, что в конечном счете приведет к неустойчивому состоянию работы С/С.

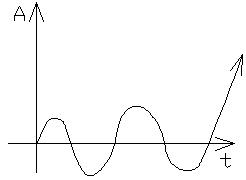
Электрическая аналогия колебательного звена.

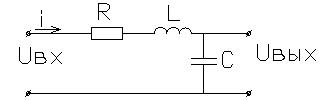
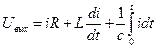
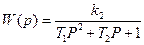
Т₁, Т₂ – постоянные времени

K₂ – коэффициент усиления колебательного звена

4. Дифференцирующее звено

Идеальным дифференцирующим звеном называется звено в котором выходная величина пропорциональна скорости изменения входной величины

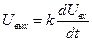
K – коэффициент передачи дифференцирующего звена

Уравнение реального диф. Звена в общем случае может быть представлено в след. виде:

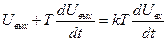
Т – постоянная времени звена

K – коэффициент передачи звена

В реальных САР наибольшее распространение получили дифференцирующие трансформаторы, мостовые схемы.

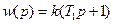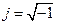p=jw 0<w<∞

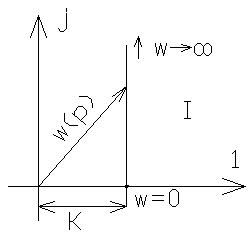
5. Дифференцирующее звено 2-го порядка

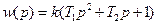
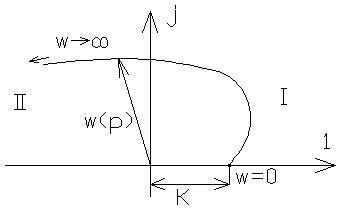
6. Интегрирующее звено

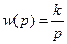
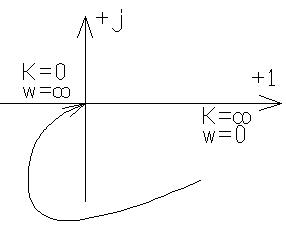
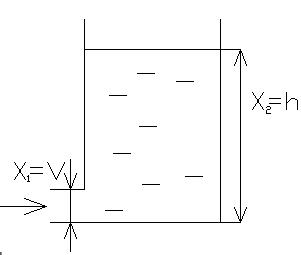
Входная величина – это объем поступающей воды, а выходная – уровень воды в сосуде. Таким образом способность изменения выходной величины пропорционально входной величине.

7. Звено транспортного запаздывания.

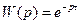
τ – время запаздывания

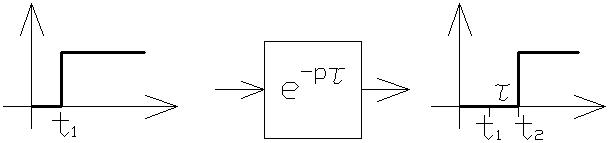
τ=t₂-t₁

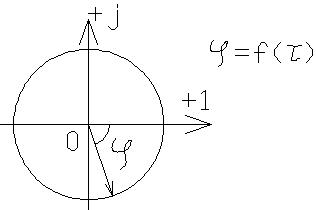
Таким образом соединением апериодического звена 2-го порядка со звеном транспортного запаздывания годограф объединенной С/С поворачивается по часовой стрелке на угол φ пропорционально времени запаздывания τ.

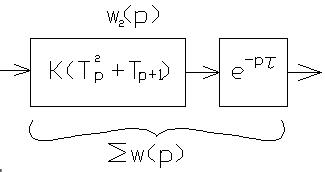
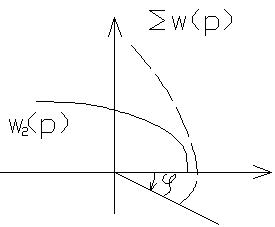
Звено транспортного запаздывания негативно влияет на устойчивость С/С, т.е. устойчивость ухудшается.

§Логарифмические частотные характеристики

Исследование САР намного упрощается, если пользоваться не обычными амплитуда-фазовыми характеристиками (АФЧХ - это годографы С/С), а логорифмическими частотными характеристиками.

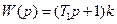
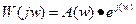
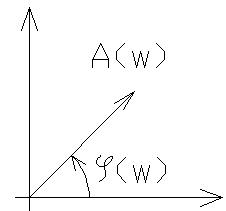
Кривые соответствующие функциям lnA(w) и φ(w) построенные в ln масштабе частот, называется логарифмическими амплитудной и фазовой частотными характеристиками.

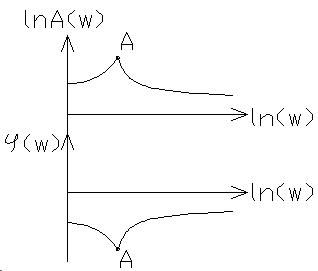
т. А – точка перегиба или резонанса частот

§ Операции с элементарными динамическими звеньями.

САР состоит из элементарных звеньев, которые могут образовывать различные соединения, основными из которых являются последовательное и параллельное соединение звеньев. Кроме этого соединения могут охватываться обратной связью, в таком случае они образуют замкнутую С/С. А когда не охватываются обратной связью, то образуют разомкнутую С/С.

Считается, что элементарные звенья обладают направленным действием, т.е. нисходящие звенья практически не связывают воздействие на предыдущие звенья.

1). Последовательное соединение

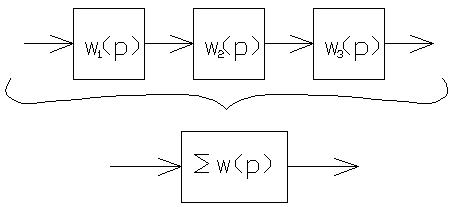
2). Параллельное

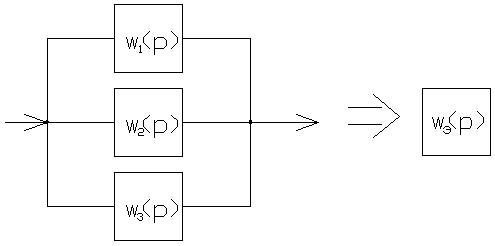
Для С/С с обратной связью

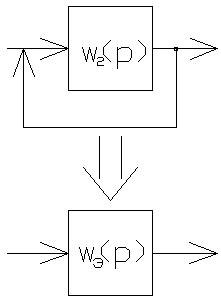
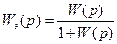
Обратная связь применяется для повышения устойчивости работы С/С. Чаще всего для этого используется отрицательная обратная связь.

Устойчивость С/С САР.

Под управлением САР понимается перевод С/С из некоторого неустойчивого состояния в устойчивое. В общем виде характеристическое уравнение, описывающее состояние САР записывается:

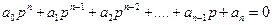
Где:

a₀, a₁,…a_n – коэффициенты, которые описывают параметры САР

Для повышения устойчивости, мы можем воздействовать на некоторые из этих коэффициентов. Таким образом при исследовании устойчивости определить параметры характеристического уравнения и по ним определить знак вещественной части.

Корневой метод оценки устойчивости С/С заключается в том, что если все параметры имеют отрицательные вещественные части и таким образом располагаются в левой части полуплоскости на комплексной плоскости, то С/С в таком случае будет являться устойчивой.

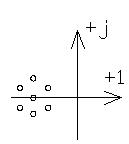
Этот метод подходит для определения устойчивости С/С не выше 3-го порядка. Однако часто для определения устойчивости достаточно определиться только в отрицательности вещественных частей корней, поэтому представляется целесообразным воспользоваться другими, более простыми методами определения устойчивости, основанными на установлении факта «-» вещественных корней уравнения без нахождения их значений. Такие методы основываются на использовании критерия устойчивости и выделении областей устойчивости.

В теории автоматического регулирования и управления наибольшее распространение получили следующие критерии устойчивости:

1. Алгебраические критерии устойчивости Рауса и Гурвица

2. Частотные критерии устойчивости Михайлова и Найквиста

3. Условия устойчивости, определяемые lg частотными характеристиками (ЛЧХ)

Критерии устойчивости Рауса - Гурвица

Корни характеристического уравнения связаны с коэффициентами этого уравнения по теореме Виета. Алгебраические критерии устойчивости позволяют установить факт «-» корней по результатам математических действий над коэффициентами характеристического уравнения. Условия, устанавливающие факт «-» корней и будут являться критериями устойчивости.

Пусть дано характеристическое уравнение следующего вида:

Если все коэффициенты этого уравнения «+», то вещественные части всех корней будут «-» в том случае, когда все диагональные миноры главного определителя будут «+».

Главный определитель составляется так, что по главной диагонали выписываются коэффициенты уравнения начиная с a₁ в возрастающем порядке до a_n. И от каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими индексами.

Места в матрице коэффициентов с индексами >n и <0 заканчиваются нулями.

Пример:

Пусть дано характеристическое уравнение 3-го порядка следующего вида:

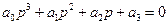
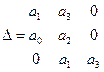
Условие Гурвица:

При 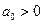и

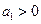
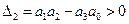
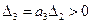
Критерий устойчивости Гайсса и Гурвица: С/С будет устойчива, когда все коэффициенты характеристического уравнения «+» и диагональный минор 2-го порядка >0.

Критерий Михайлова

Он дает возможность судить об устойчивости по годографу, описываемому концом характеристического вектора замкнутой С/С.

Критерий Михайлова формируется следующим образом: замкнутая С/С устойчива в том случае, когда характеристический вектор при изменении от 0 до ∞ проходит в «+» направлении m-квадрантов комплексной плоскости начиная своё движение от «+» вещественной полуоси, при этом нигде не обращаясь в 0.

Критерий Найквиста

Критерий Найквиста, основанный на использовании частотных характеристик позволяет определить устойчивость замкнутой С/С автоматического регулирования по амплитудно-фазовой характеристике разомкнутой С/С.

Преимуществом этого критерия является то, что амплитудно-фазовая характеристика разомкнутой С/С и её звеньев может быть построена не только расчетным, но и эксперементальным путем.

Замкнутая С/С является устойчивой, если устойчива разомкнутая С/С и её АФХ не охватывает точку с координатами (-1; j0)

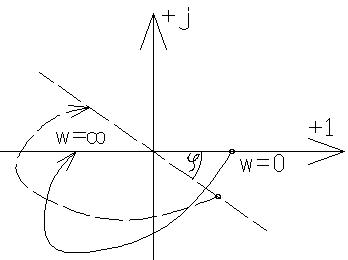
Устойчивости САУ с запаздыванием

Так как умножение комплексного числа на величину e^-jwτ

где τ – время запаздывания, означает поворот вектора на угол ωτ можно сказать, что частичное запаздывание снижает устойчивость замкнутой С/С.

§ Структурная устойчивость САУ

Структурная схема САУ состоит из звеньев. Число, свойства и характер соединений выбирается исходя из требований статических и динамических характеристик С/С. Помимо типовых динамических звеньев в состав С/С могут входить и другие звенья. Формирующая, звено с обратным статизмом и т.д.

Структуроустойчивой называется такая С/С, которая может быть сделана устойчивой путем выбора соответствующих параметров без изменения ее структуры.

Структурноустойчивая С/С будет не устойчивой при особых значениях параметров и ее можно сделать устойчивой только путем изменения структурной схемы.

Качество С/С управления и формирования их структур

§ Показатели качества регулирования

В большинстве практических случаев устойчивость не является достаточным условием нормального функционирования С/С в зависимости от необходимого технологического режима САУ должна обеспечивать требуемое качество работы установки в переходных режимах. Качество регулирования определяется следующими основными параметрами:

1. Величиной перерегулирования

2. Быстродействием (временем регулирования)

3. Числом колебаний регулируемой величины за время переходного процесса

Перерегулированием называется разности между max и становившимся отклонениями регулируемой величины к установившемуся отклонению.

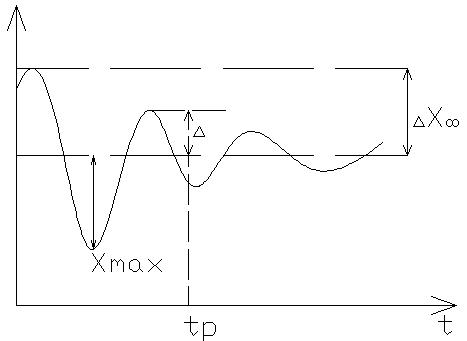
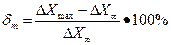
Допустимое перерегулирование определяется конкретными условиями работы и назначением САУ. Для С/С работающих при задающем воздействии обычно допускают δ_m=18-25%. А для С/С поддержания определенного значения регулируемой величины, работающих при возмущающих воздействиях, значения могут достигать гараздо больших величин.

Быстродействие представляет собой время, в течение которого отклонение регулируемой величины превышает некоторое допустимое значение, т.е.

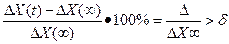
Число колебаний регулируемой величины N за время переходного процесса

Это число колебаний за время переходного процесса t_p обычно принимают не более трех колебаний.

Точность

Под точностью понимается степень приближения действительного выходного сигнала X и его задающему значению X₀.

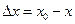называют ошибкой САУ

Установившаяся ошибка обработки постоянного сигнала называется статической ошибкой.

Текущая ошибка обработки переменного сигнала называется динамической ошибкой САУ. Динамическая ошибка С/С изменяется с течением времени. Она зависит от структуры, параметров и характера изменений воздействия в САУ. Статическая ошибка определяется структурными параметрами и величиной постоянного воздействия САУ.

Статическая ошибка замкнутой САУ может быть определена непосредственно по передаваемой функции С/С, путем приравнивания оператора p к нулю (p=0).

При оценке качества переходных процессов в САУ могут быть применены прямые и косвенные методы.

Наиболее достоверные данные можно получить прямым методом по кривой переходного процесса. Такая кривая переходного процесса может быть найдена экспериментальным, расчетным путем, либо моделированием (MATLAB).

Расчет переходного процесса производится на основании дифференциального либо операторного уравнения С/С. Такие уравнения могут быть составлены на основании структурной схемы, состоящей из элементарных звеньев.

Возможны и другие методы расчета, например метод, основанный на использовании вещественно-частотной характеристика.

В случае уравнений более высоких порядков определение корней уравнения расчетным путем является трудоемкой задачей.

§ Интегральные методы оценки качества регулирования

Интегральные методы позволяют по некоторым определенным интегралам вида:

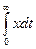
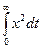
Судить о быстродействии и колебательности процесса.

Метод интегральных ошибок заключается в определении параметров С/С, соответствующих min интегральной ошибке.

Оценка быстродействия по линейной интегральной ошибке

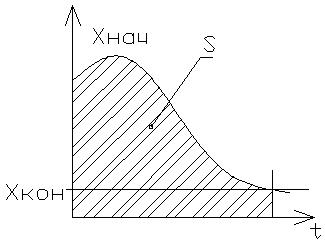
Процесс получается наиболее качественным и быстродействующим в случае минимизации площади S (это минимум линейной интегральной ошибки)

В идеальном случае процесс перехода из одного состояния X_нач в другое X_кон происходил бы мгновенно и площадь, характеризующая линейную интегральную ошибку S была бы =0. В реальных же условиях при апериодическом процессе интегральная ошибка зависит от интенсивности снижения величины X.

Интегральная ошибка тем меньше, чем меньше время регулирования t.

В случае колебательного процесса или же наличия перерегулирования, необходимо применять квадратичную интегральную ошибку.

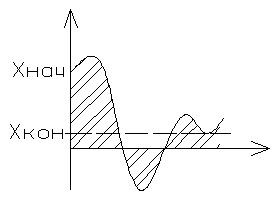
§ Постановка задач формирования структур САУ

Под синтезом понимается определение структуры и параметров регуляторов САУ в соответствии с ее целевым назначением и требуемыми параметрами качества функционирования.

САУ состоит из объекта управления и управляющего устройства.

В С/С управления электроприводами объект управления включает двигатели различных типов, передаточные звенья от вала двигателя к механизму, преобразователи одного вида энергии в другой и т.д.

Основным показателем для выбора элементов оборудования объекта управления является род тока, мощность, напряжение, частота питающего напряжения, требуемое передаточное число редуктора и т.д.

Состав объекта управления, его математическая модель и параметры должны быть определены до синтеза С/С.

Математическая модель объекта может быть представлена дифференциальным, операторным уравнениями, либо структурной схемой.

Исходными данными для синтеза С/С является статическая и динамическая точности С/С.

На первом этапе проектирования САУ определяется структура С/С, которая зависит от функционального назначения С/С. В основу структура ложится один из фундаментальных принципов управления, т.е. по отклонению, возмущению, или же комбинированный принцип.

При необходимости адаптации, система дополняется контуром адаптивного управления.

На практике наибольшее распространение получило управление по отклонению, в связи с его главным свойством – самовыравниванием. Т.е. способностью нормально функционировать при возникающих возмущениях.

Чтобы построить структуру С/С управления надо определить, что является выходной величиной, как воздействовать на объект, чтобы управлять этой величиной в определенных пределах, как получить информацию о значениях выходной величины (какие датчики мы можем поставить), каковы возмущающие и задающие воздействия. Если же объектом управления является электрический привод компрессора (вентилятора), а выходной величиной является производительность компрессора (вентилятора), т.е. скорость вращения двигателя компрессора (вентилятора), то надо выяснить, как управлять этой скоростью.

В случае частотного управления используется частотные контроллеры с управляемыми транзисторами большой мощности. В качестве датчиков скорости используются преимущественно бесконтактные схемы на основе подсчета пульсаций за 1 оборот.

Во многих случаях задающее воздействие формируется как программное управление с учетом критериев оптимальности.

1-ый критерий оптимальности характерный для холодильных С/С – это поддержание определенной температуры в холодильной камере при наличии возмущающих воздействий и при min энергозатратах.

Окончательный выбор структуры С/С выполняется с учетом возможностей технической реализации, а так же чувствительности к возмущениям и помехоустойчивости на основании результатов математического регулирования.

§ Выбор структуры системы управления пуско-тормозными режимами.

В качестве главного критерия оптимальности САУ должно быть принято быстродействие, а в некоторых случаях принимается условие min потерь энергии за цикл управления работы электропривода.

При формировании процессов запуска и торможения, а в случае реверсирования двигателя так же и реверса, должно быть учтено требование обеспечения max производительности.

Блочная схема пуска, останова и реверса асинхронного электропривода:

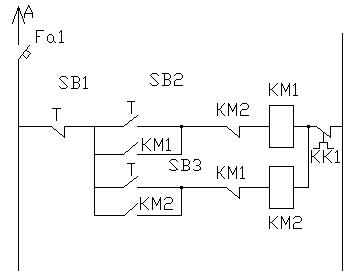
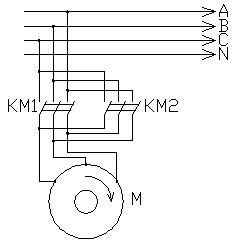
SB1 – кнопка СТОП

SB2 – кнопка ВВЕРХ

SB3 – кнопка ВНИЗ

§ Математическая постановка задачи оптимального управления

Оптимальным процессом называется наилучший в определенном смысле процесс, который не только приводит систему из начального состояние в конечное, но и удовлетворяет определенной оценке качества. Так при необходимости получить высокую производительность критерием служит быстродействие, а при необходимости экономии энергии – min потерь энергии и min затрат энергии. Обычно критерии оценивают процесс в целом, ставя ему в соответствие определенное численное значение. Таким образом, устанавливается взаимно-однозначное соответствие между множеством функции времени или же процессов и множеством соответствующих этому процессу чисел (критерий качества). Такое соответствие называется функционал. Задача оптимального управления имеет решение лишь в том случае, когда объект обладает свойством управляемости.

Объект называется полностью управляемым в какой-то определенной области, если же для любой пары точек внутри области, таких как: X₀=X(t₀); X_f=X(t_f)

В этой области существует допустимое управление U, которое за время t_f-t₀ переводит объект из т. X₀ в объект X_f. Свойство управляемости практически означает возможность формирования любого требуемого процесса путем надлежащего выбора сигнала управления.

§ Синтез регулятора С.О.

Выбор метода определяется структурой САУ, которая может быть одноконтурной, либо многоконтурной. Одноконтурная структура имеет одну главную отрицательную обратную связь по выходной координате охватывающую все звенья прямого канала. Корректирующее устройство таких систем обычно включается последовательно со звеньями прямого канала и соответственно с обратной связью образовывают регулятор. Критерием качества работы системы: заданное значение перерегулирования (max динамического отклонения по температуре, скорости нарастания температуры или ее убывания, а так же быстродействие в переходном режиме). Многоконтурные системы характеризуются наличием кроме главной отрицательной обратной связи, еще и несколькими обратными связями по различным переменным составляющих САУ. Синтез регуляторов таких систем состоит из двух этапов:

1. Этап определения структуры системы;

2. Этап определения параметров регулятора в зависимости от выбранного типа переходного процесса.

Синтезируемые таким образом системы обладают высокими качественными показателями переходных процессов и гарантируют заданную точность регулирования.

§ Синтез многомерных С/С

Многомерной (многосвязной) называется система, имеющая 2 или более входных и 2 или более выходных величин.

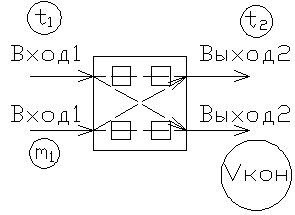
Примером многомерной системы является система управления поточным холодильным агрегатом на промысловом судне, в этом случае система управления различными техническими агрегатами связаны через охлаждаемый материал. В этом случае каждый агрегат имеет свою систему управления, но поскольку агрегаты связаны единым технологическим процессом, то и сигнал управления должен формироваться с учетом координации работы отдельных агрегатов.

ТЕМА: Линейные, цифровые и импульсные системы автоматического управления.

Системы импульсного действия имеют управляющее воздействие не непрерывное, а в виде серий импульсов. Система называется импульсной (дискретной) если она содержит хотя бы одно импульсное звено.

Импульсным звеном (модулятором) называется динамическое звено преобразующее непрерывный сигнал в последовательность импульсов. Импульсные звенья отличаются способом модуляции:

1. Амплитудно-импульсная модуляция (АИМ)

2. Широтно-импульсная модуляция (ШИМ)

3. Время-импульсная модуляция (ВИМ)

В свою очередь ВИМ бывает:

1. Частотно-импульсная модуляция (ЧИМ)

2. Фазоимпульсная модуляция (ФИМ)

В зависимости от способа модуляции, амплитуда, ширина, фаза или же частота импульсов пропорциональна величине входного сигнала в соответствующие моменты времени. Остальные же параметры импульсов остаются постоянными. Помехоустойчивость возникает потому, что хотя бы один из параметров импульса остается постоянным. Наиболее благоприятный для них режим – переключение. Импульсная модуляция хорошо используется так же для управлением силовыми полупроводниковыми приборами.

Блочная схема импульсной САУ

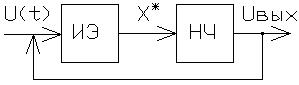
ИЭ – импульсный элемент

НЧ – непрерывная часть САУ

В этой схеме ИЭ включен в сеть основного воздействия последовательно с эквивалентным звеном непрерывной части (НЧ) САУ. В дальнейшем будем рассматривать непрерывную часть как линейную НЧ. Для упрощения исследования линейных САУ, целесообразно представить импульсный элемент состоящий из двух частей:

1. Идеального импульсного элемента (ИИЭ)

2. Формирующего звена (ФЗ)

Блочная схема ИЭ

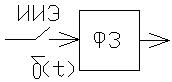
ИИЭ – в виде переключателя преобразует непрерывную величину X(t) в последовательность импульсов следующих друг за другом через равные интервалы времени и представляющий собой δ-функцию.

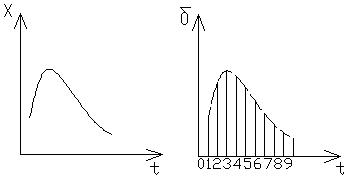
Величина каждой δ-функции, т.е. интеграл от нее по времени, пропорционально значению непрерывной величины в моменты замыкания ключа. Формирующее звено преобразует каждый ИИ в импульс конкретной формы. Чаще всего импульсы имеют форму прямоугольников.

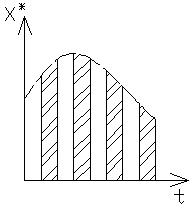
§ Синтез цифровых С/С

Цифровой называется система, управление в которой осуществляется с помощью цифровых вычислительных устройств. Кроме цифровых применяются цифро-аналоговые системы, в состав управляющего устройства которых наряду с цифровыми устройствами входят звенья непрерывного действия, т.е. аналоговые звенья.

Входными данными для цифрового устройства управления могут быть: задающий сигнал и сигнал обратной связи, который преобразуется в выходной сигнал управления, представлены в двоичной системе счисления.

Преимущество цифрового управления перед непрерывным заключается в высокой помехоустойчивости и точности, а так же в возможности создания однотипных цифровых элементов сложных С/С управления сложными технологическими процессами.

Цифровые устройства управления могут быть построены на основе программной или аппаратной реализации.

В случае аппаратной – преобразование входных данных в сигнал управления осуществляется по алгоритму, зависящему от электрических соединений между элементами цифрового устройства.

В случае программной реализации – преобразование входных данных в сигнал управления осуществляется путем вычисления по программе, записанной в память компьютера.

Вычислительное устройство предназначенное для управления – это специализирует ЭВМ и называется контроллером (микропроцессор).

Блочная схема системы с программной реализацией цифрового управления.

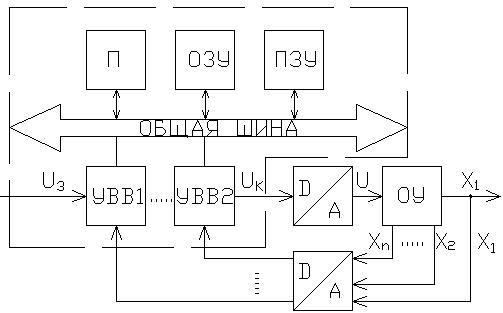
П – процессор

ОЗУ – оперативно-запаминающее устройство

ПЗУ – постоянно-запоминающее устройство

УВВ1…УВВ_n – устройство ввода и вывода информации

D/A – цифро-аналоговый и аналогово-цифровой преобразователь

ОУ – объект управления

X₁…X_n – переменная состояния

U_з – задающее воздействие

Процессор выполняет вычислительные сигналы правления по программе, хранящейся в ПЗУ. ПЗУ защищено от несанкционированного доступа, путем программных средств. Исходная информация для вычисления служит задающим воздействием УЗ. Информация о переменном состоянии поступающая по каналам обратной связи, а так же основные параметры для расчета (формулы хранящиеся в памяти компьютера). В результате полученного сигнала управления U_к в виде двоичного кода, который затем после цифро-аналогового преобразователя преобразует сигнал управления Y, понятный объекту управления. Как аппаратная, так и программная реализация управления имеет преимущества и недостатки. Аппаратная реализация обладает более высоким быстродействием, недостатком его является отсутствие гибкости системы, т.к. переход к другому алгоритму потребует изменение в электрической схеме устройства управления. Преимуществом программной реализации является гибкость устройства управления, которая выражается в возможности изменять алгоритм управления программным путем, не изменяя электрической схемы устройства. Недостаток – низкое быстродействие, поскольку время обработки информации зависит от времени выполнения командных программ, которые в свою очередь определяются тактовой частотой процессора.

Случайные процессы в САУ

Случайные процессы называются случайными процессами времени, т.е. такая функция, которая в каждый момент времени описывается случайно величиной. Случайные процессы так же называются вероятностными или стохастическими. В природе имеют место различные случайные процессы. В динамических системах случайные процессы возникают под действием случайных воздействии. Они характеризуются изменением координат, которые в этом случае представляют случайную функцию времени. Конкретный случайный процесс называется реализацией. Для изучения случайных процессов используют вероятностные характеристики. Наиболее полно случайный процесс может быть определен с помощью функцией распределения вероятностного значения случайного процесса в различные моменты времени. Функцией распределения вероятности случайного процесса могут быть одномерными и многомерными. Одномерный дифференциальный закон распределения вероятности случайного процесса характер этого процесса в произвольный момент времени. С помощью этого закона получаем представление о случайном процессе в любой момент времени из имеющегося диапазона от нуля до t.

Случайный процесс:

Рис.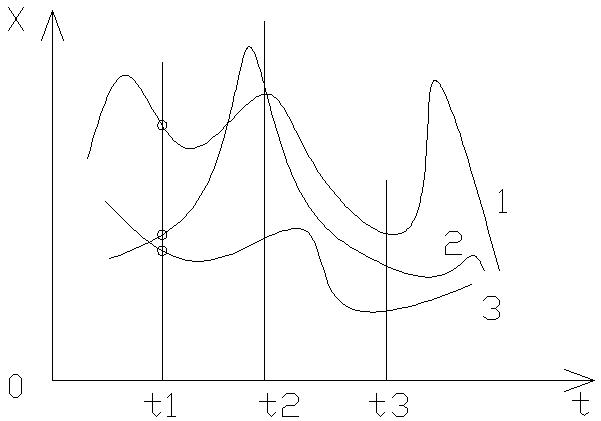

Дифференциальная функция разветвления вероятности

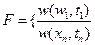
Характеризует вероятность появления в этот момент времени соответствующего значения искомой величины X.

Корреляционная функция

Корреляция характеризует степень тесноты связей между двумя переменными. Коэффициент корреляции может изменяться от нуля до 1. В случае коэффициента корреляции r=0 связь между переменными отутствует

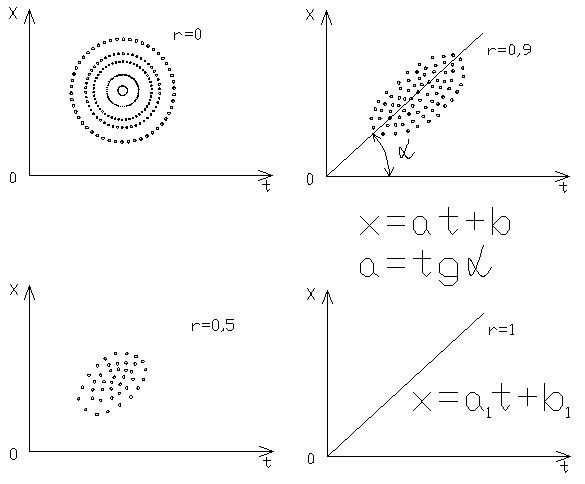
Корреляционная функция является мерой взаимной связи между значениями случайной функции x(t₁) и x(t₂) разделенной интервалом времени τ.

При больших значениях τ x(t₁) и x(t₂) можно считать независимыми случайными величинами, с уменьшением времени τ взаимосвязь этих величин возрастает и степень их взаимной связи, определяется корреляционной функцией. Функция в таком случае имеет вид:

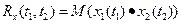
Корреляционная функция представляет собой математическое ожидание произведения значений случайной функции в моменты времени t₁ и t₂. Корреляционная функция отображающая связь значений одной и той же случайной функции называется автокорреляционной. Существует взаимно-корреляционная функция, которая показывает связь значений двух случайных функции x(t) и y(t).

R_xy(t₁,t₂)=M(x(t₁)y(t₂))

Случайные процессы обычно делятся на стационарные и нестационарные.

Стационарным называется процесс x(t), если его n-мерная плотность вероятности ω_n(x₁, x₂ … x_n; t₁, t₂ … t_n) при любом n зависит от величины интервала t₂-t₁ и не зависит от положения этих интервалов области изменения аргумента t. Случайные процессы которые не попадают под определение стационарных по отношению к нестационарным. Больших нестационарных процессов обладают эргодичностью. Общим свойством эргодичных процессов является то, что статические характеристики полученные усреднением по времени при достаточно большом интервале наблюдения первой реализации совпадают с характеристиками полученными усреднением по множеству реализации для фиксированного момента времени. Другими словами, наблюдение случайного процесса на первом объекте в течение достаточно длительного времени. Дает в среднем ниже результаты, что и наблюдение проведенного в одно и то же время на большом числе объектов первого типа.

§ Особенности нелинейных систем и основные типы нелинейности.

Нелинейной называется система среди элементов, в который есть хотя бы один с нелинейной зависимостью между ее выходными и входными сигналами.

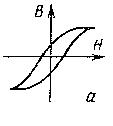
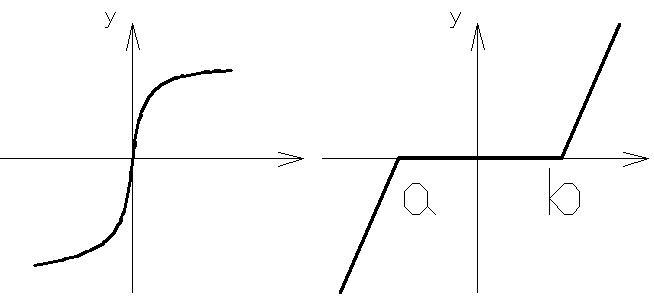
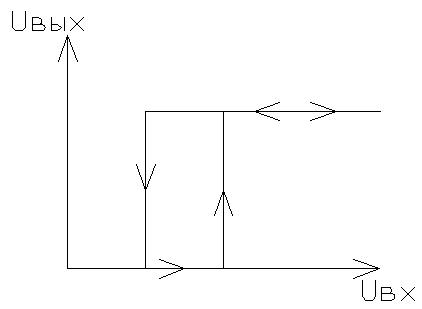
В таких нелинейных системах процессы в большинстве случаев не могут исследованы методами линейной теории. Для нелинейных систем характерна работа в режимах принципиально неосуществимых в линейной системе. К таким режимам относится смена состояния равновесия в зависимости от начальных условий, автоколебания, дискретное изменение амплитуды сигналов, изменение частоты вынужденных колебаний, зависимость частоты автоколебаний от частоты внешнего воздействия, подавление слабого сигнала сильным.

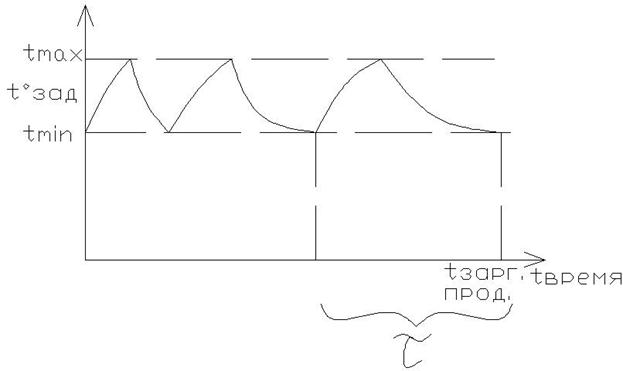
График измененения температуры в камере холодильника компрессора, который включается релейным линейным элементом.

Блочная схема холодильной установки.

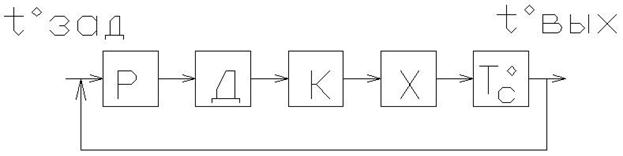
Р – реле включения двигателя

Д – двигатель компрессора (однофазный, асинхронный)

К – компрессор

Х – камера холодильника

Т_с⁰ – датчик температуры, который измеряет температуру в камере.

Данная блочная схема работает в режиме автоколебаний, частота которых зависит от массы и температуры охлаждаемого продукта, от температурных установок датчика температуры Т_с⁰, от хладопрозводительности компрессора холодильника.

Адаптивные системы

При решении технических задач связанных с использованием самоприспосабливающихся систем (СПС). Принципиальное значение имеет классификация по характеру процесса адаптации.

Классификация адаптивной системы.

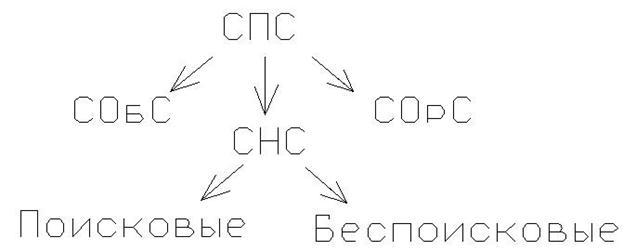
СНС – самонастраивающиеся системы представляют собой системы, в которых адаптация при изменении условий работы осуществляется путем изменения параметров и управляющих воздействий.

Самоорганизующиеся системы – это системы, в которых адаптация осуществляется за счет изменения не только параметров и управляющих воздействий, но так же и структуры системы. Самоорганизующиеся системы для своего функционирования используют меньший объем априорной информации по сравнению с самонастраивающимися системами, поэтому они являются системами более сложного типа. Самообучающиеся системы СОбС – это системы автоматического управления, в которых оптимальный режим работы управления объекта определяется с помощью управляющих устройств, алгоритм работы которого автоматически целенаправленно совершенствуется в процессе обучения путем автоматического поиска. Поиск производится с помощью второго управляющего устройства, который является органической частью самообучающийся системы. СНС делятся на поисковые (экстремальные) и беспоисковые (аналитические). В поисковых системах, изменение параметров управления устройства или же управляющее воздействие осуществляется в результате поиска условий экстремума определенных показателей качества.

Поиск условий экстремума осуществляется в результате пробных воздействий по оценке полученных результатов. В беспоисковых системах определение параметров управляющего воздействия производится на основе аналитического определения условий обеспечивающих определенное качество управления без применения специальных поисковых сигналов. Важным достоинством беспоисковых систем является отсутствие беспоисковых движений и поэтому время самонастройки у беспоисковых самонастраивающихся систем, намного меньше, чем у поисковых систем. При применении адаптивных систем решают следующие основные задачи:

1. В процессе функционирования системы управления при изменении параметров структуры и внешних воздействий обеспечивается такое управление, при котором сохраняется заранее определенные динамические и статические свойства систем.

2. В процессе проектирования и наладки при начальном отсутствии полной информации о параметрах структуры объекта управления и внешних воздействий автоматической настройки системы в соответствии с определенными динамическими и статическими свойствами систем.

Экстремальные системы позволяют таким образом обеспечивать поддержание показателей качества процесса на экстремальном значении не только при первоначальной настройке, но и при сдвиге экстремума в процессе работы.

§ Применение нечеткой логики для синтеза систем управления.

Методы нечеткой логики относятся к области искусственного интеллекта и применяются к нечетким множествам. Нечеткое множество А, определяется функцией принадлежности М_а(x) который указывает степень принадлежности элемента X множеству А. Эта функция изменяется от нуля до 1 (0≤ М_а(x) ≤1).

Границы нечеткого множества размыты к относительности его элементов. Нету точных данных об их принадлежности к данному множеству. Применяя нечеткие множества можно осуществить переход от числовых к лингвистическим переменным. Числовые переменные обеспечивают высокую точность, которая целесообразна, если имеются точные исходные данные и необходимо получить точные результаты. Лингвистические элементы дают возможность применять математические аппараты к исходным данным, которые заданны неточно и если результат не требует высокой точности, при этом нечеткие алгоритмы управления позволяют определять управляющий сигнал на основании нечетких значений рассогласования и сигналов обратных связей. Применение такого управления целесообразно для объектов, динамического свойства, который плохо изучаем или же поврежден изменениями, а высокой точности и быстродействия не требует. Преимущество нечеткого управления является простая его реализация программными методами, а так же возможность обеспечить удовлетворительное качества при удовлетворительном качестве воздействия.

Дата добавления: 2014-01-11