Определение значимости показателей качества

Практические указания по выполнению задачи №6

Дано: Сравнить четыре варианта возможной реализации измерительного преобразователя по пяти показателям качества и выбрать лучший из них, если условия применения системы характеризуются следующим рядом ранговых соотношений этих показателей: d = l > S > С > V.

Табл. 1.

Показатели	Оценки показателей качества вариантов изделия
качества	I	II	III	IV
V
C
d
S
l´10^-6

Анализ оценок вариантов системы (табл. 1) показывает, что среди них нет ни одного явно предпочтительного по всем показателям качества. Чтобы решить, какой из рассмотренных вариантов является лучшим, необходимо:

Øопределить значимость показателей качества;

Øпривести все оценки к единой безразмерной системе оценивания;

Øсвести многокритериальную задачу к однокритериальной.

Последовательность решения второй задачи представлена в п.п. 1-3.

Показатели качества, как частные, так и общие, имеют различную значимость для конкретных условий использования системы. Поэтому в зависимости от условий работы каждому показателю назначается определенный вес – коэффициент значимости k_j, где j = 1,.. n, n – количество показателей, по которым проводится сравнение вариантов решений. Коэффициент значимости k_j характеризует степень влияния показателя на принятие решения, его важность относительно других показателей. При этом должно соблюдаться нормирующее условие [3]:

. (2)

Задача определения значений коэффициентов значимости показателей является весьма сложной, поскольку точных математических методов ее решения нет, и на этом этапе принятия решения вносится субъективизм (произвол!). Для снижения степени субъективизма в назначении коэффициентов k_j применяют метод попарного сравнения важности показателей. В соответствии с этим методом составляется квадратная матрица размерностью n ´ n. В столбце и строчке, ограничивающих матрицу, располагаются в одинаковой последовательности показатели. Элементами этой матрицы являются коэффициенты предпочтимости е_rj, соответствующие знакам “ > ”, “ = ”, “ < ” и равные 1,5; 1,0; 0,5. Определяются коэффициенты предпочтимости путем попарного сопоставления показателей и выявления наиболее важного из двух.

По окончания сравнения показателей подсчитываются величины относительных приоритетов Р_отнj показателей, каждый из которых равен сумме всех элементов матрицы в соответствующей строке:

(3)

Далее вычисляются значения абсолютных приоритетов каждого показателя по формуле:

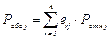(4)

Величина коэффициента значимости j-го показателя определяется выражением:

. (5)

В домашней задаче варианты сравниваются по пяти показателям (n = 5), а условия применения системы заданы рядом ранговых соотношений показателей качества: d = l > S > С > V. В этом случае матрица предпочтимости имеет размерность 5´5 (табл. 2).

Определим по этой таблице коэффициент значимости, например, показателя d. Величина относительного приоритета этого показателя в соответствии с (3) равна:

Р_отн (d) = 1,0+1,0+1,5 + 1,5 + 1,5 = 6,5.

Величина абсолютного приоритета этого показателя в соответствии с (4) равна:

Р_абс (d) = 1,0×6,5 + 1,0×6,5 + 1,5×5,0 + 1,5×4,0 + 1,5×3,0 = 31,0.

Коэффициент значимости показателя Q в соответствии с (5) равен:

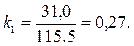
При вычислении коэффициентов значимости k_i полученные результаты следует округлить так, чтобы их сумма была равна 1, чтобы выполнялось нормирующее условие (2).

Табл. 2.

Матрица предпочтимости показателей качества
Показа-тели	d = l > S > С > V	Ротн	Рабс	kj
d l S С V	1,0 1,0 1,5 1,5 1,5 1,0 1,0 1,5 1,5 1,5 0,5 0,5 1,0 1,5 1,5 0,5 0,5 0,5 1,0 1,5 0,5 0,5 0,5 0,5 1,0	6,5 6,5 5,0 4,0 3,0	31,0 31,0 22,0 17,5 14,0	0,27 0,27 0,19 0,15 0,12
Суммы			115,5	1,000

Дата добавления: 2014-01-11