
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрический смысл метода сопряженного направления
|
|
|
|
|

Применение H равно сильно повороту осей эллипсов так, чтобы одна из осей проходила через точку А 1 (А2) т.е. за один шаг мы попали на главную ось и следующим шагом попадаем в extr. Вычислять на каждом шаге.
Метод сопряженных градиентов, тоже что и метод сопряженных направлений, только 1-ый шаг делается не в произвольном направлении, а по градиенту.
В технике, как правило, задачи на extr всегда имеют некоторые дополнительные ограничения.
Если задача ставится так:
1.  . Найти её extr на ограничениях равенствах
. Найти её extr на ограничениях равенствах  . Примечание. Ограничений типа
. Примечание. Ограничений типа  здесь нет, то это классическая задача Лагранжа.
здесь нет, то это классическая задача Лагранжа.
2. Вторая задача (неклассическая).  . Найти extr на ограничениях –неравенствах
. Найти extr на ограничениях –неравенствах  .
.
Задача линейного программирования
Как мы уже говорили ранее, термин «линейное программирование» связывается с исследованием и решением следующей типовой задачи.
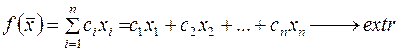
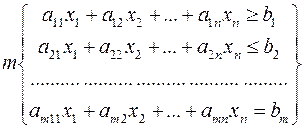
|
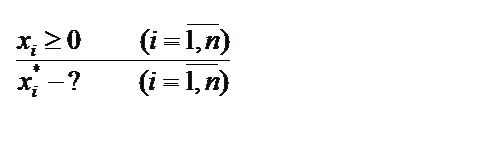
 Видно, что в ограничениях стоят соотношения ≥, ≤, =. При решении задачи ЛП эту систему из «m» ограничений сводят к системе из m уравнений, что легко сделать введя добавочные переменные
Видно, что в ограничениях стоят соотношения ≥, ≤, =. При решении задачи ЛП эту систему из «m» ограничений сводят к системе из m уравнений, что легко сделать введя добавочные переменные  так, чтобы в зависимости от знака неравенства имело место одно из двух выражений:
так, чтобы в зависимости от знака неравенства имело место одно из двух выражений:

Такие изменения просто приводят к увеличению числа переменных, что непринципиально.
Итак, ограничения запишутся виде:
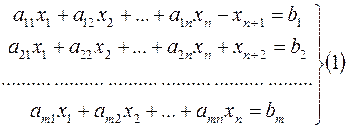
Обозначим для удобства 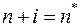 и задачу ЛП запишем:
и задачу ЛП запишем:
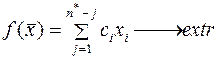


Характерной особенностью задачи является то, что число уравнений меньше числа неизвестных т.е.  . Введем некоторую терминологию, широко употребляемую в задачах ЛП.
. Введем некоторую терминологию, широко употребляемую в задачах ЛП.
Базисом называется любой набор переменных таких, что определить, составленный из коэффициентов при этих переменных, не равен нулю. Эти 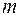 переменных называются базисными переменными (по отношению к данному базису). Остальные
переменных называются базисными переменными (по отношению к данному базису). Остальные 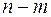 переменных называются небазисными или свободными переменными. В каждой конкретной системе уравнений (1) может существовать несколько различных базисов с различными базисными переменными.
переменных называются небазисными или свободными переменными. В каждой конкретной системе уравнений (1) может существовать несколько различных базисов с различными базисными переменными.
Если положить все свободные переменные равными нулю и решить полученную систему 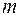 уравнений с
уравнений с 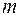 неизвестными, то получим базисное решение. Однако среди различных базисных решений будут такие, которые дают отрицательные значения некоторых переменных. Эти базисные решения противоречат условию задачи и являются недопустимыми.
неизвестными, то получим базисное решение. Однако среди различных базисных решений будут такие, которые дают отрицательные значения некоторых переменных. Эти базисные решения противоречат условию задачи и являются недопустимыми.
Допустимые базисные решения дают неотрицательные значения базисных переменных. Допустимые базисные решения являются наиболее простыми из возможных решений системы (1).
ЛП возникло в связи с рассмотрением вопросов о нахождении наивыгоднейших вариантов при решении различны управленческих и планово производных задач. К таким задачам относятся задачи нахождения наиболее рационального способа использования сырья и материалов, определения наивыгоднейших производственных режимов, повышения эффективности работы транспорта и т. п.
Рассмотрим, например, следующею задачу об использовании ресурсов. Для осуществления  различных технологических процессов
различных технологических процессов  заводу требуется
заводу требуется 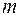 видов ресурсов
видов ресурсов  (сырьё, топливо, комплект инструментов и т.п.). Запасы ресурсов каждого вида ограничены и равны
(сырьё, топливо, комплект инструментов и т.п.). Запасы ресурсов каждого вида ограничены и равны 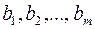 . Известен расход ресурсов на единицу продукции по каждому технологическому процессу. Требуется определить в каком количестве выпускать продукцию каждого вида, чтобы доход от реализации этой продукции был максимальным.
. Известен расход ресурсов на единицу продукции по каждому технологическому процессу. Требуется определить в каком количестве выпускать продукцию каждого вида, чтобы доход от реализации этой продукции был максимальным.
Обозначим через  расход ресурсов вида
расход ресурсов вида  на единицу продукции вида
на единицу продукции вида  , а через
, а через 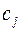 - доход от реализации единицы продукции вида
- доход от реализации единицы продукции вида  . Все имеющиеся данные представим в виде таблицы, положив в конкретности
. Все имеющиеся данные представим в виде таблицы, положив в конкретности 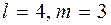 .
.
| Виды ресурсов | Расход ресурсов на ед. продукции | Запасы ресурсов | |||
| T1 | T2 | T3 | T4 | ||
| S1 | а11 | а12 | а13 | а14 | b1 |
| S2 | а21 | а22 | а23 | а24 | b2 |
| S3 | а31 | а32 | а33 | а34 | b3 |
| Доход от реализации ед. продукции | С1 | С2 | С3 | С4 | ______ |
Обозначим через  количество единицы выпускаемой продукции вида
количество единицы выпускаемой продукции вида  . Ограничениями в этой задаче являются требования, чтобы расход ресурсов вида
. Ограничениями в этой задаче являются требования, чтобы расход ресурсов вида  на выпуск всех видов продукции не превышал имеющихся запасов:
на выпуск всех видов продукции не превышал имеющихся запасов:
 .
.
Эти ограничения легко превратить в уравнения, введя переменную 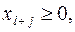 которые можно трактовать как использованные ресурсы вида
которые можно трактовать как использованные ресурсы вида  . При этом получим
. При этом получим

Добавим сюда очевидное  .
.
Доход от реализации выпускаемой продукции
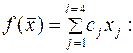
Оптимальным планом выпуска продукции будет такое неотрицательное решение (2), при котором целевая функция 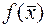 будет максимальна.
будет максимальна.
Для того, чтобы получить более полное представление о задаче линейного программирования, дадим геометрическую интерпритацию следующей задачи.
Имеется система уравнений
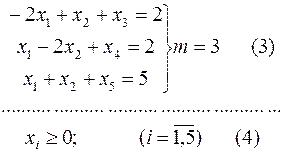
Целевая функция  . Требуется найти неотрицательные значения переменной удовлетворяющих (3) и максимизирующих целевую функцию (5).
. Требуется найти неотрицательные значения переменной удовлетворяющих (3) и максимизирующих целевую функцию (5).
В данном примере число уравнений 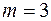 , а число неизвестных
, а число неизвестных  , так что имеется
, так что имеется 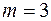 базисных переменных и
базисных переменных и 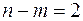 свободных переменных. То, что число свободных переменных равно 2, дает возможность проиллюстрировать решение задачи геометрически в 2-х мерном пространстве, т.е. на плоскости.
свободных переменных. То, что число свободных переменных равно 2, дает возможность проиллюстрировать решение задачи геометрически в 2-х мерном пространстве, т.е. на плоскости.
Систему (3) можно разрешить относительно 3-х переменных, например,  выразив их через
выразив их через  и
и  .
.
При это получим:

По условию задачи ЛП переменная может принимать только неотрицательные значения, т.е. областью допустимых значений переменной будут область определяемая условиями (4). Каждое из неравенств (4) определяет некоторую полуплоскость на плоскости 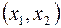 . Так неравенство
. Так неравенство  определяет правую полуплоскость, а неравенство
определяет правую полуплоскость, а неравенство  определяет полуплоскость, лежащую по одну сторону от прямой
определяет полуплоскость, лежащую по одну сторону от прямой  а именно ту, которая содержит начало координат, что легко проверяется подстановкой в первое из соотношений (6) координат точку (0,0) область, соответствующая
а именно ту, которая содержит начало координат, что легко проверяется подстановкой в первое из соотношений (6) координат точку (0,0) область, соответствующая  т.е. слева от
т.е. слева от  является запрещенной. Из рисунка, приведенного ниже, видно, что допустимой областью значений переменной
является запрещенной. Из рисунка, приведенного ниже, видно, что допустимой областью значений переменной  и
и  является замкнутый выпуклый многоугольник o a b c d.
является замкнутый выпуклый многоугольник o a b c d.
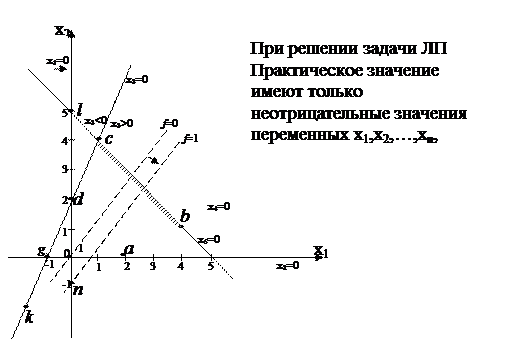
Рис.1
Проведенное построение позволяет дат геометрическую интерпретацию базисному решению. Т.к. каждая прямая на рисунке соответствует обращению в нуль одной из переменной, то в точках пересечения 2-х прямых будут обращаться в нуль две, т.е. в нашем случае 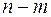 переменных. Но
переменных. Но 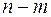 есть число свободных переменных, обращения которых в нуль соответствует базисному решению. Таким образом, точки пересечения прямых
есть число свободных переменных, обращения которых в нуль соответствует базисному решению. Таким образом, точки пересечения прямых 
 определяют базисное решение задачи ЛП (т.т. о, a, b, c, d, e, f, g, n, k).
определяют базисное решение задачи ЛП (т.т. о, a, b, c, d, e, f, g, n, k).
Среди базисных решений имеются такие, которые не принадлежат области допустимых решений. Это недопустимые базисные решения (т.т., e, f, g, n, k). Области допустимых решений принадлежат только те точки пересечения прямых  , которые являются вершинами многоугольника допустимых решений. Следовательно, вершины многоугольника допустимых решений соответствуют допустимым базисным решениям.
, которые являются вершинами многоугольника допустимых решений. Следовательно, вершины многоугольника допустимых решений соответствуют допустимым базисным решениям.
Рассмотрим теперь условия обращения в «max» и формулы (5) геометрически при любом 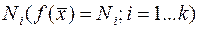 . Выражение (5) определяет прямую, проведенную под углом 450 к оси абсцисс, причем увеличению
. Выражение (5) определяет прямую, проведенную под углом 450 к оси абсцисс, причем увеличению 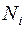 соответствует перемещению прямой в направлении стрелки, показанной на рисунке 1. Это прямая будет совместна с допустимым решением задачи только в том случае, если она имеет общие точки с областью допустимых решений. Максимальное значение
соответствует перемещению прямой в направлении стрелки, показанной на рисунке 1. Это прямая будет совместна с допустимым решением задачи только в том случае, если она имеет общие точки с областью допустимых решений. Максимальное значение 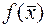 получается при крайнем положении прямой, когда она только касается многоугольника допустимых решений. Ясно, что такая прямая обязательно проходит хотя бы через одну из её вершин, которые, как мы видим, соответствует допустимым базисным решениям. (Отметим, что если бы, скажем, прямая
получается при крайнем положении прямой, когда она только касается многоугольника допустимых решений. Ясно, что такая прямая обязательно проходит хотя бы через одну из её вершин, которые, как мы видим, соответствует допустимым базисным решениям. (Отметим, что если бы, скажем, прямая  , бала бы параллельной
, бала бы параллельной  , то тогда бы линия целевой функции достигла max значения на линии
, то тогда бы линия целевой функции достигла max значения на линии  , т.ею сразу двух вершин (a b n - мерном случае – и более) и решениями были бы бесчисленные множества точек на участке a b).
, т.ею сразу двух вершин (a b n - мерном случае – и более) и решениями были бы бесчисленные множества точек на участке a b).
Таким образом, мы приходим к очень важному выводу, что решение задач ЛП, обращается в extr Ц.Ф. 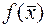 , обязательно лежит среди допустимых базисных решений. Кстати, этой вывод легко обобщается на случай произвольных
, обязательно лежит среди допустимых базисных решений. Кстати, этой вывод легко обобщается на случай произвольных 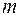 и
и  , когда
, когда  . Полученный вывод позволяет наметить путь решения задачи ЛП. Поскольку решение должно находится среди допустимых базисных решений, число которых, то можно найти все допустимые базисные решения и для каждого из них вычислить значение
. Полученный вывод позволяет наметить путь решения задачи ЛП. Поскольку решение должно находится среди допустимых базисных решений, число которых, то можно найти все допустимые базисные решения и для каждого из них вычислить значение 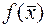 . Окончательным решением явится то из найденных решений, для которого значения
. Окончательным решением явится то из найденных решений, для которого значения 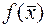 будет
будет  .
.
Такой путь решения задачи хотя и возможен, но весьма трудоемок, т.к. число допустимых базисных решений может быть весьма большим. Однако существуют рациональные способу последовательного перебора базисных решений, которые позволяют рассматривать не все допустимые базисные решения, а их минимальные число. Одним из наиболее распространенных методов такого перебора является так называемый симплексный метод.
Существо Симплекс –метода состоит в следующем. Прежде всего, находится какое–либо допустимое базисное решение. Его можно найти, приняв какое–либо 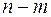 переменных за свободные приравняв их нулю и решив получившуюся систему уравнений (1) т.е. получив значения базисных переменных. Если при этом некоторые из базисных переменных окажутся отрицательными, то нужно выбрать другие свободные переменные, т.е. перейти к новому базису.
переменных за свободные приравняв их нулю и решив получившуюся систему уравнений (1) т.е. получив значения базисных переменных. Если при этом некоторые из базисных переменных окажутся отрицательными, то нужно выбрать другие свободные переменные, т.е. перейти к новому базису.
После того, как найдено допустимое базисное решение, проверяется, не достигнут ли уже extr целевой функции 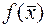 . Если нет, то ищут новое допустимое базисное решение, но не любое, а такое, которое увеличивает значение целевой функции
. Если нет, то ищут новое допустимое базисное решение, но не любое, а такое, которое увеличивает значение целевой функции 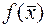 . Затем процедура повторяется. Данный метод довольно быстро приводит к цели, т.к. позволяет исключить из рассмотрения большое число базисных решений, заведомо не обращающих в extr целевую функцию.
. Затем процедура повторяется. Данный метод довольно быстро приводит к цели, т.к. позволяет исключить из рассмотрения большое число базисных решений, заведомо не обращающих в extr целевую функцию.
Разберем метод более подробно на рассмотренном ранее примере (3)-(5).
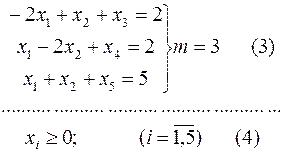

Поскольку 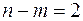 , то в качестве свободных переменных можно взять любые две переменные, например,
, то в качестве свободных переменных можно взять любые две переменные, например,  и
и  .
.
Положив их равными нулю, из (3) находим базисное решение  ,
,  которое является допустимым и при котором
которое является допустимым и при котором
 .
.
Проверку того, не достигнут ли при найденном решении extr (в данном случае max) целевой функции, можно сделать путем поиска нового базисного решения, при котором целевая функция будут больше. Для перехода к новому допустимому базисному решению одну из свободных переменных  или
или  следует сделать базисной. При этом, т.е. после перевода её из свободных, когда она была =0, в базисные, она согласно (4) будет отличной от нуля, т.е. возрастает. Следовательно, если какие-либо из свободных переменных входит в выражение для целевой функции со знаком «+», а значит при её увеличении целевой функции возрастает, то «max» целевой функции не достигнут и данную переменную следует превратить в базисную, сделать её отличной от нуля. Вместо этой переменной, переведенной из свободной в базисную, надо из старого базиса перевести одну из переменных в свободную. Но какую именно?
следует сделать базисной. При этом, т.е. после перевода её из свободных, когда она была =0, в базисные, она согласно (4) будет отличной от нуля, т.е. возрастает. Следовательно, если какие-либо из свободных переменных входит в выражение для целевой функции со знаком «+», а значит при её увеличении целевой функции возрастает, то «max» целевой функции не достигнут и данную переменную следует превратить в базисную, сделать её отличной от нуля. Вместо этой переменной, переведенной из свободной в базисную, надо из старого базиса перевести одну из переменных в свободную. Но какую именно?
Однако при возрастании свободной переменной некоторые из базисных переменных начнут уменьшатся, причем одни из них при возрастании этой свободной переменной достигнут нуля раньше, другие позднее. Так как отрицательные значения переменной недопустимы, в качестве новой свободной переменной в замен той свободной, которую мы только что перевели в базисную, которая раньше других обратится при этом в нуль.
В рассматриваемом примере в выражении для целевой функции (5) со знаком «+» входит свободная переменная  . Значит «max» целевой функции не достигнут и переменную
. Значит «max» целевой функции не достигнут и переменную  следует сделать из свободной базисной. Для определения новой свободной переменной взамен
следует сделать из свободной базисной. Для определения новой свободной переменной взамен  , перешедшей в базисные, выразим старые базисные переменные
, перешедшей в базисные, выразим старые базисные переменные  через сиарые свободные
через сиарые свободные  и
и  , приведя уравнение (5) к (6).
, приведя уравнение (5) к (6).

Из этих уравнений видим, что если положить свободную переменную 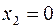 (а свободные переменные для базисного решения и должны быть равны нулю),то при увеличении
(а свободные переменные для базисного решения и должны быть равны нулю),то при увеличении  переводимой из свободных в новые базисные,
переводимой из свободных в новые базисные,  не уменьшается, а уменьшается
не уменьшается, а уменьшается  и
и 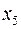 ,причем с ростом
,причем с ростом  переменной
переменной  быстрее достигнет нулю, чем
быстрее достигнет нулю, чем 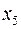 .
.  обратится в нуль при
обратится в нуль при  , а
, а 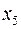 при
при  . Таким образом, её переменная
. Таким образом, её переменная  и сделаем новой свободной вместо
и сделаем новой свободной вместо  , что приводит нас к новому базису
, что приводит нас к новому базису  .
.
Для продолжения решения преобразуем (3) к виду, когда новые базисы переменных  зависят от новых свободных переменных
зависят от новых свободных переменных  и
и  . Из 2-го уравнения системы (6) сразу получаем:
. Из 2-го уравнения системы (6) сразу получаем:
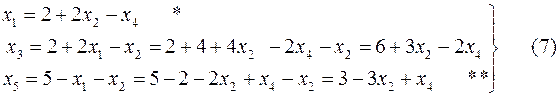
Целевую функцию также выразим через новые свободные переменные  и
и 
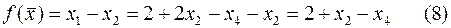
Повторив приведенные ранее рассуждения, приходим к выводу, что «max» целевой функции не достигнут т.к.  входит в (8) со знаком «+». Значит надо свободную переменную
входит в (8) со знаком «+». Значит надо свободную переменную  перевести в базисную, а какую базисную надо перевести в свободные вместо
перевести в базисную, а какую базисную надо перевести в свободные вместо  ?
?
Обратимся к (7) когда свободная переменная  , то видно, что при возрастании новой базисной переменной
, то видно, что при возрастании новой базисной переменной  переменные
переменные  и
и  не уменьшаются, а
не уменьшаются, а 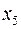 уменьшается. Её и переведем из базисных в свободные. Итак, новый базис
уменьшается. Её и переведем из базисных в свободные. Итак, новый базис 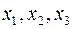 , новые свободные переменные
, новые свободные переменные  и
и 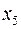 . Разрешая (7) относительно новых базисных переменных
. Разрешая (7) относительно новых базисных переменных  и
и 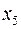 , получим
, получим

Целевая функция при этом принимает вид
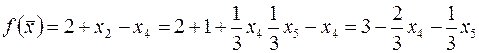
Из этого выражения видно, что при увеличении свободной переменных  и
и 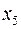 значение
значение 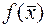 уменьшается. Следовательно при данном базисе достигается «max». Целевой функцией
уменьшается. Следовательно при данном базисе достигается «max». Целевой функцией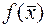 и решением поставленной задачи будет следующий набор переменных
и решением поставленной задачи будет следующий набор переменных


При этом  .
.
Рассмотренный метод решения задачи линейного программирования обладает тем недостатком, что связан с громоздкими преобразованиями системы линейных уравнений из одной формы в другую. Значительного упрощения преобразований можно добиться, если представлять уравнения в виде таблиц, содержащих коэффициенты при переменной (так называемая табличная форма симплекс-метода). Переход от одной системы уравнений к другой при этом сводится к пересчету коэффициентов в таблицах, что осуществляется по чисто формальным правилам, хорошо приспособленным для решения на ЭВМ. Программы решения задач линейного программирования входят в математическое обеспечение большинства ЭВМ.
Классическая задача Лагранжа

На l найти точку, из которой отрезок АВ виден под наибольшим углом. Это типичная задача Лагранжа. Она может решаться двумя путями: 1-путь- путь перебора, что является неэффективно;
2-путь –построение линий равного уровня угла 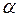 .
.
 т.е. в точке касания.
т.е. в точке касания.

Решение задачи на ограничениях будет единственно тогда, когда 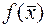 и
и  есть функции выпуклые или вогнутые.
есть функции выпуклые или вогнутые.
Решение находится в точке касания линий уравнения и ограничения. А как найти решение аналитически?
Возьмем:
Найти 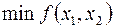 на ограничении
на ограничении  =0
=0
|


точка А0 абсолютно безусловный 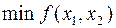 и пусть она не лежит на ограничении.
и пусть она не лежит на ограничении.
Предположим, что 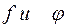 - гладкие выпуклые функции.
- гладкие выпуклые функции.
Решение задачи будет на линии уровня, касающейся ограничения.
Проведем общую касательную к 2-м кривым.
 и
и 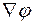 в extr точки лежат на одной линии т.е. на перпендикулярной к обшей касательной.
в extr точки лежат на одной линии т.е. на перпендикулярной к обшей касательной.
Из подобия треугольников имеем:
 или в виде 2-х равенств:
или в виде 2-х равенств:
 Это из геометрии для экстремума точки
Это из геометрии для экстремума точки

(1)
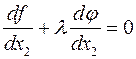
Составим функцию Лагранжа:
 Скалярное произведение
Скалярное произведение

Специально по сконструированная функция 
1-ое слагаемое
2-ое слагаемое произведение 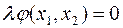 .
.
Найдем безусловный extr такой функции.
По теореме Ферма.
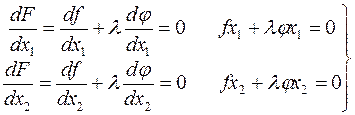 тоже самое что (*)
тоже самое что (*)
 уравнение связи.
уравнение связи.
Имеем три уравнения и три неизвестные -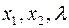
 - неопределенное множество Лагранжа.
- неопределенное множество Лагранжа.
С помощью  задача на условный extr нелинейной функции сводится к задачи на безусловный extr функции Лагранжа.
задача на условный extr нелинейной функции сводится к задачи на безусловный extr функции Лагранжа.
Мы (поскольку имеем необходимый условный extr) находим точки, подозрительные на extr.
Пример.
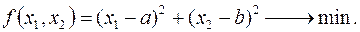
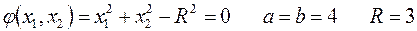

Конструируем вспомогательную функцию.
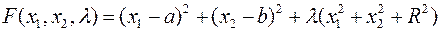
Данную функцию исследуем на extr.
 Если система совместна, то она имеет единственное решение.
Если система совместна, то она имеет единственное решение.

Подставим  и
и  в уравнение 3
в уравнение 3
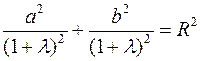 : откуда
: откуда
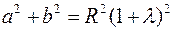
Находим:



Откуда:
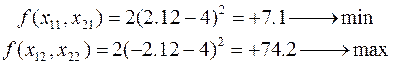
|


Если много ограничений
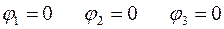 тогда
тогда

Такие задачи бывают несовместны т.к. иногда ограничения экранируют друг друга

Пример:
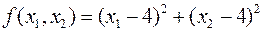

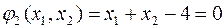

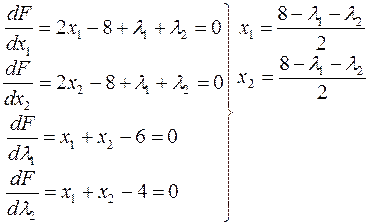
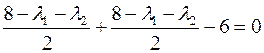

Откуда:
 Видно, что эти уравнения несовместимы.
Видно, что эти уравнения несовместимы.
Из рисунка видно, что  экранирует
экранирует  т.е. второе ограничение здесь не работает.
т.е. второе ограничение здесь не работает.

Поэтому, когда ограничений много проще вычисляя точки находить решение для каждого ограничения.
Какие задачи можно решить методом Лагранжа из тех, которые были поставлены? Можно решать задачу распределения мощностей.
Пример.
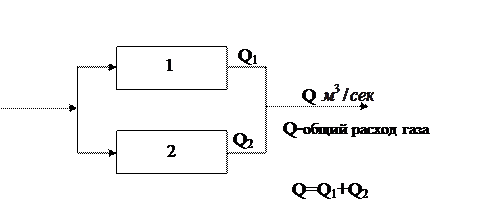
Мощность, затрачиваемая на перекачку  , где
, где
 -характеризуют состояние мощности гидр. цепей (трубопроводы, задвижки, колена и т.д).
-характеризуют состояние мощности гидр. цепей (трубопроводы, задвижки, колена и т.д).
Здесь могут быть две постановки задачи:
1) При ограничении равенства  обеспечить
обеспечить  N (т.е.
N (т.е. 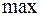 к.п.д.).
к.п.д.).
2) При заданной мощности агрегатов обеспечить 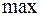 производительности.
производительности.
Решим задачу методом Лагранжа.




Пусть 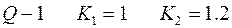
Тогда,  т.е. так необходимо распределить мощности между машинами, чтобы обеспечить
т.е. так необходимо распределить мощности между машинами, чтобы обеспечить  N.
N.
Т.к. нагрузка меняется, то меняется и Q (пунктир). Для каждого режима заранее находится точки режима (0) и используют его при изменении нагрузки. 
2) Задана  получить
получить 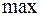 производительность.
производительность.
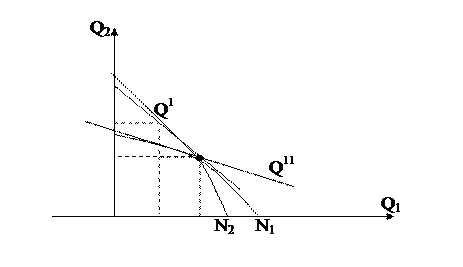
Пример. Имеем последовательное соединение машин, когда надо сильно поднять давление.
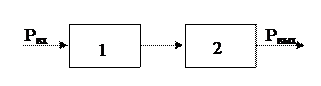 Ei - степень старения
Ei - степень старения

 уравнение связи.
уравнение связи.
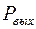 должен быть постоянным
должен быть постоянным 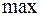 при
при  .
.
Отсюда видно, чтобы обеспечить это должно быть  .
.
Мощность машин
 где
где
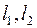 -такие же коэффициенты, как
-такие же коэффициенты, как  и
и 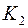 т.е. характеризуют состояние машин, их изношенность, производительность и т.д.
т.е. характеризуют состояние машин, их изношенность, производительность и т.д.
Постановка задачи:
1) Задано 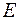 , получить
, получить 
 .
.
2) Задано  , получить
, получить 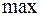
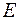 .
.


Из физики работы 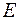 не может быть отрицательным поэтому нам надо брать одно значение
не может быть отрицательным поэтому нам надо брать одно значение  , а именно «-».
, а именно «-».
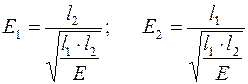

Пусть 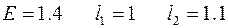 , тогда
, тогда  .
.
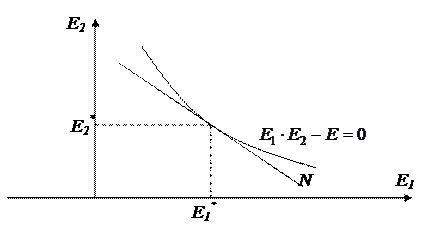
Задача Лагранжа в технике имеет ограниченное применение. Поэтому в технике чаще рассматриваются задачи.
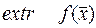 на
на 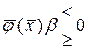 т.е. на ограничениях неравенства.
т.е. на ограничениях неравенства.
Нет общих аналитических методов решения этих задач, только численные или в частных случаях аналитические.
Проанализируем эти задачи качественно. Нам для этого понадобятся новые математические понятия.
Пусть дано уравнение:
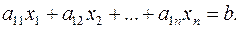
Это уравнение называется уравнением гиперплоскости.
Гиперплоскость - множество точек, удовлетворяющих этому уравнению.
Пусть есть нелинейное уравнение.
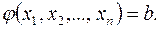 Это гиперповерхность –множество точек, удовлетворяющих этому решению.
Это гиперповерхность –множество точек, удовлетворяющих этому решению.
В 2-х мерном пространстве гиперплоскость это прямая линия, а гиперповерхность – кривая.
Возьмем

Это неравенство характеризует полупространство, т.е. множество точек, удовлетворяющих этому неравенству. Это открытое (незамкнутое) полупространство.
Возьмем
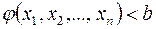 - это неравенство характеризует открытое полупространство, т.е. множество точек, удовлетворяющих этому неравенству.
- это неравенство характеризует открытое полупространство, т.е. множество точек, удовлетворяющих этому неравенству.
Проведем операцию замыкания:
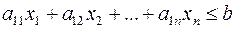 т.е. полупространство включаем и гиперплоскость. Получим замкнутое полупространство, т.е. множество точек, удовлетворяющему этому неравенству.
т.е. полупространство включаем и гиперплоскость. Получим замкнутое полупространство, т.е. множество точек, удовлетворяющему этому неравенству.
Также
 тоже характеризует замкнутое полупространство.
тоже характеризует замкнутое полупространство.
Свойство этих множеств (полупространств) зависит от свойств функции  .
.
В множествах также различают выпуклые и невыпуклые множества.
Теорема. Замкнутые множества, образованные выпуклыми или вогнутыми функциями, являются выпуклыми.
Определение выпуклости множества
 , т.е. любые две точки множества и отрезок их соединяющий должны принадлежать множеству.
, т.е. любые две точки множества и отрезок их соединяющий должны принадлежать множеству.

Теорема конструктивна, ибо всегда мы можем определить выпуклая функция или нет.
Теорема. Пересечение выпуклых  является выпуклым множеством.
является выпуклым множеством.

Если берут 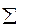 множеств, т.е.
множеств, т.е. 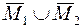 то уже нельзя сказать о выпуклости
то уже нельзя сказать о выпуклости  множеств.
множеств.
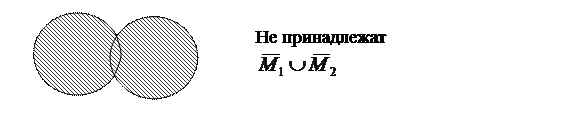
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 414; Нарушение авторских прав?; Мы поможем в написании вашей работы!
