
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод динамического программирования
|
|
|
|
В течение 50-х годов XX века американский математик Р. Беллман и ряд его сотрудников развили новый общий метод решения вариационных задач, названный или динамическим программированием. Этот метод пригоден для оптимизации любых сложных систем, описываемых не только дифференциальными уравнениями с ограничениями на переменной, или без них, но и другим математическим аппаратом, включая различные статические системы, СМО и экономические системы.
МДП по своей идее значительно отличается от классического вариационного исчисления и принципа максимума Понтрягина. Методика решения последними двумя способами заключается в том, что оптимальная траектория считается уже каким то образом найденной известной. Затем вся эта оптимальная траектория варьируется целиком, в целом их множества проварьируемых траекторий находится оптимальная.
В МДП принят иной путь нахождения оптимальной траекторий, который заключается в том, что оптимальная траектория и соответствующая ей уравнение ищутся на отдельных участках или ступенях. Иными словами, проще разбиваются на несколько ступеней, на каждой стоится множество траекторий и соответствующих им управлений. Теперь казалось бы достаточно перебрать все траектории, и выбрать оптимальную, но это нерациональный титанический труд. Создатели МДП пошли другим путем – на каждой стадии они выбирают оптимальную и отбрасывают неоптимальные, бесперспективные участки траекторий (на отдельной стадии для участка это сделать много легче, чем для траектории в целом). При этом оказывается, что отбрасывается не только не оптимальный кусочек траектории на этой стадии, но и вся траектория в целом, которые в своем составе имеют неперспективный кусочек на рассматриваемой стадии. Выбор оптимальной траектории при этом ставится намного легче и короче.
Для подтверждения сказанного рассмотрим статическую задачу по выбору оптимальной траектории.
Пример.
Пусть между пунктами 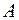 и
и 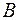 следует проложить железную дорогу или шоссейную минимальной стоимости. Рельеф местности очень сложный и предварительные изыскания показали, что если дорогу проложить по прямой
следует проложить железную дорогу или шоссейную минимальной стоимости. Рельеф местности очень сложный и предварительные изыскания показали, что если дорогу проложить по прямой  , её стоимость будет очень высокой. Геодезисты и экономисты рассмотрели отдельные сравнительно простые для строительства участки между
, её стоимость будет очень высокой. Геодезисты и экономисты рассмотрели отдельные сравнительно простые для строительства участки между 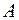 и
и 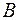 и определили стоимость строительства этих участков. Стоимость строительства дороги будет суммой стоимости строительства этих участках. Данную задачу можно решить перебором всех возможных траекторий между
и определили стоимость строительства этих участков. Стоимость строительства дороги будет суммой стоимости строительства этих участках. Данную задачу можно решить перебором всех возможных траекторий между 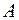 и
и 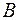 и выбрать самую дешевую. Однако этот путь практически необозрим. По этому найдем по пути МДП. Разобьем весь район строительства на стадии, из которых до начальной
и выбрать самую дешевую. Однако этот путь практически необозрим. По этому найдем по пути МДП. Разобьем весь район строительства на стадии, из которых до начальной 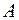 или конечной
или конечной 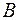 точек можно попасть за одинаковое количество шагов. В МДП решение начинается с конца и хотя в нашем случае начало
точек можно попасть за одинаковое количество шагов. В МДП решение начинается с конца и хотя в нашем случае начало 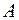 и конец
и конец 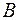 неразличимы, по традиции МДП решение начинается с конца
неразличимы, по традиции МДП решение начинается с конца 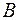 . Рассмотрим переход стадии
. Рассмотрим переход стадии 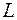 к точке
к точке 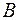 . Причем нас совершено не интересует предыстория движения, т.е. каким образом мы попали на стадию
. Причем нас совершено не интересует предыстория движения, т.е. каким образом мы попали на стадию 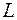 , но уже если попали в точку
, но уже если попали в точку  или
или 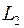 , то попасть в точку
, то попасть в точку 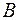 мы можем за один шаг с затратами 8 из точки
мы можем за один шаг с затратами 8 из точки  или 9 из точки
или 9 из точки 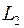 . Эти затраты и ставим в соответствующие кружочки. Других траекторий из стадии
. Эти затраты и ставим в соответствующие кружочки. Других траекторий из стадии 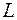 в точку
в точку 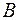 нет.
нет.
Сдвинемся еще на шаг назад на стадию 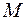 и проанализируем траектории, по которым а точку
и проанализируем траектории, по которым а точку 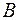 можно попасть за два шага из точки
можно попасть за два шага из точки 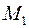 до стадии
до стадии 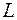 можно попасть единственным образом
можно попасть единственным образом 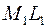 , а в точку
, а в точку 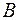 за два шага можно попасть по единственной траектории
за два шага можно попасть по единственной траектории  и стоимость это го участка 8 денежных единиц. А из точки
и стоимость это го участка 8 денежных единиц. А из точки  до стадии
до стадии 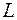 можно попасть единственным образом
можно попасть единственным образом 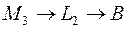 и стоимость этого участка 25 д. ед. А из точки
и стоимость этого участка 25 д. ед. А из точки  до стадии
до стадии 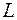 можно попасть двумя путями
можно попасть двумя путями  (стоимость 10 д.ед.) и
(стоимость 10 д.ед.) и 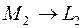 (стоимость 11 д.ед.). И здесь на стадии (а не на всей траектории) очень легко выбрать оптимальный путь (
(стоимость 11 д.ед.). И здесь на стадии (а не на всей траектории) очень легко выбрать оптимальный путь ( ) и отвергнуть бесперспективный (
) и отвергнуть бесперспективный (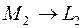 ). При этом отвергается не только бесперспективный путь
). При этом отвергается не только бесперспективный путь 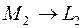 , но и все траектории, исходящие из точки
, но и все траектории, исходящие из точки 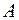 и включающие участок к
и включающие участок к 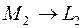 . В кружочек
. В кружочек  поставим наименьшую стоимость пути
поставим наименьшую стоимость пути 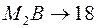 д.ед.
д.ед.
Продолжая понятное движение и отсекая неперспективные траектории, доходим до точки 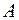 , из которой до стадии
, из которой до стадии 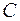 два пути
два пути  и
и  , отсекая неоптимальный путь
, отсекая неоптимальный путь  , выбираем наилучший
, выбираем наилучший  , стоимостью в 4 д.ед.
, стоимостью в 4 д.ед.
Теперь двигаемся из точки 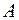 по не отвергнутым траекториям, мы выбираем оптимальный путь
по не отвергнутым траекториям, мы выбираем оптимальный путь 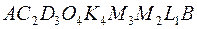 , стоимостью
, стоимостью 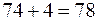 д.ед.
д.ед.
Понятно, что отвергая неперспективные маленькие участки между стадиями, мы тем самым, не проделывая непосредственно этого, отвергаем все неоптимальные траектории, включающие в себя этот отвергнутый участок т.е. эффективность выбора оптимальной траектории очень высока.
Обратимся теперь к шестой типовой задаче управления, т.е. к динамической задаче в которой объект управления характеризуется уравнением 
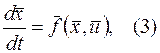 .
.
Причем 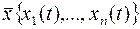 -вектор координат состояния
-вектор координат состояния
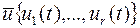 - вектор управления
- вектор управления
Пусть 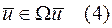 и требуется минимизировать интеграл
и требуется минимизировать интеграл
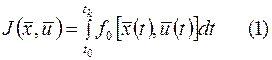
В основе МДП лежит принцип оптимальности. Этот принцип сформулирован Р. Беллманом для широкого круга систем, будущее поведение которых полностью определяется их состоянием в настоящем. Поэтому оно не зависит от характера их «предыстории», т.е. поведение системы в прошлом, коль скоро система находится в данный момент в данном состоянии. Для иллюстрации рассмотрим оптимальную траекторию в 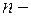 мерном фазовом пространстве с начальным и конечным значением вектора
мерном фазовом пространстве с начальным и конечным значением вектора 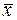 , равным
, равным  при
при 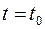 и
и 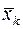 при
при 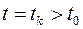 .
.
Пусть начальное условие  заданы, значение
заданы, значение 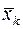 , вообще говоря, не известно.
, вообще говоря, не известно.
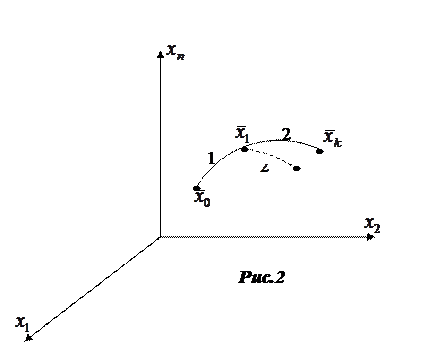
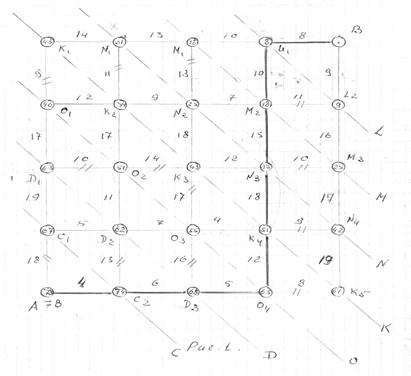
Отметим какую-либо промежуточную точку 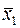 , траектории, соответствующую
, траектории, соответствующую 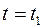 ,где
,где  и назовем участок траектории от
и назовем участок траектории от  до
до 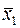 первым, а от
первым, а от 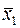 до
до 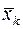 - вторым.
- вторым.
Второму участку соответствует часть интеграла (1), равная
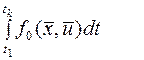
Второй участок траектории может рассматриваться и как самостоятельная траектория. Она будет оптимальной, если соответствующий ей интеграл минимален. Принцип оптимальности можно сформулировать так:

Это означает, что в том случае, когда начальное состояние системы есть 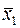 , а начальный момент времени
, а начальный момент времени 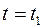 , то не зависимо от того, каким образом пришла система к этому состоянию. Ее оптимальным последующим движением будет траектория 2. Действительно допустим противное – тогда критерий (1), рассматриваемый для интервала времени от
, то не зависимо от того, каким образом пришла система к этому состоянию. Ее оптимальным последующим движением будет траектория 2. Действительно допустим противное – тогда критерий (1), рассматриваемый для интервала времени от 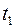 до
до 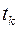 , будет наименьшим не для траектории 2, а для какой-либо иной траектории
, будет наименьшим не для траектории 2, а для какой-либо иной траектории 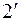 , исходящей из точки
, исходящей из точки 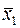 и показанной пунктиром на рис.2. Но в этом случае можно было бы построить «лучшую» траекторию, чем траектория 1-2, и для первоначальной задачи, нужно лишь выбрать управление
и показанной пунктиром на рис.2. Но в этом случае можно было бы построить «лучшую» траекторию, чем траектория 1-2, и для первоначальной задачи, нужно лишь выбрать управление 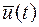 таким, чтобы описываемая траектория 1, а затем
таким, чтобы описываемая траектория 1, а затем 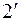 . Между тем мы исходим из того, что траектория 1-2 оптимальна. Противоречие доказывает невозможность существования траектории
. Между тем мы исходим из того, что траектория 1-2 оптимальна. Противоречие доказывает невозможность существования траектории 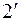 , обеспечивающее меньшее значение,
, обеспечивающее меньшее значение, 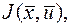 чем траектория 2. И так траектория 2 оптимальна.
чем траектория 2. И так траектория 2 оптимальна.
Сформулированный выше принцип оптимальности является весьма общим необходимым условием оптимального процесса, справедливым как для непрерывных, так и для дискретных систем.
Принцип оптимальности выглядит почти тривиальным и, на первый взгляд бедным по содержанию утверждением. Однако из него можно, как показывал Беллман, методически рассуждая вывести необходимое условие для оптимальной траектории, имеющее отнюдь не тривиальный характер. В сущности, принцип оптимальности не так уж тривиален, как может в начале показаться. Это видно хотя бы из того, что утверждение, кажущееся его обобщением: «Любой участок оптимальной траектории является оптимальной траекторией» - вообще говоря, не справедливо. Так, например, первый участок траектории 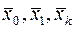 на рис.2 может сам по себе не быть оптимальной траекторией, т.е. не давать минимум интегралу
на рис.2 может сам по себе не быть оптимальной траекторией, т.е. не давать минимум интегралу 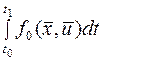 , если заданы только лишь начальные условия
, если заданы только лишь начальные условия  .
.
Поясним это утверждение элементарной иллюстрацией. Как распределяет свой силы хороший бегун при беге на длинную дистанцию? Действует ли он по принципу: Беги на каждом отрезке на столько быстро, на сколько сможешь? Конечно нет, ведь, бегун может «выдохнуться» за долго до подхода к цели. Разумно распределяя свои ресурсы в соответствии с конечной целью, бегун в начале экономит свои силы, чтобы не «выдохнуться» в конце дистанции. Аналогичным образом любое управлением не должно быть «близоруким», не должно руководствоваться лишь достижением наилучшего моментального, локального эффекта. Оно должно быть «дальновидным», оно должно быть подчинено конечной цели, т.е. минимизации функционала (1) на всем интервале от 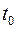 до
до 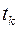 . Только в том случае, когда задана конечная точка
. Только в том случае, когда задана конечная точка 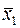 первого участка при
первого участка при 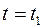 , первый участок также сам по себе является оптимальной траекторией.
, первый участок также сам по себе является оптимальной траекторией.
Можно дать и другую формулировку принципа оптимальности:
 Эквивалентность этой и предыдущей формулировок очевидно, если понимать под «предысторией» системы ту траекторию 1, по которой изображающая точка пришла в положение
Эквивалентность этой и предыдущей формулировок очевидно, если понимать под «предысторией» системы ту траекторию 1, по которой изображающая точка пришла в положение 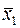 (рис.2). Под состоянием системы в рассматриваемый момент времени понимается в данном случае именно то состояние, соответствующее точке
(рис.2). Под состоянием системы в рассматриваемый момент времени понимается в данном случае именно то состояние, соответствующее точке 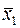 при
при 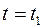 .
.
Поясним метод рассуждения Беллмана на простом принципе управляемого объекта с управлением
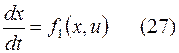 .
.
Где  – единственная координата системы:
– единственная координата системы:
 - единственное управляемое воздействие, ограниченное некоторой областью
- единственное управляемое воздействие, ограниченное некоторой областью  .
.
Пусть задано начальное условие 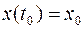 . Допустим, что требуется найти закон управления
. Допустим, что требуется найти закон управления 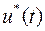 минимальный интеграл
минимальный интеграл
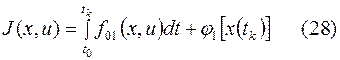
где для удобства за 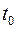 примем время равное нулю, т.е.
примем время равное нулю, т.е. 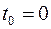 ; значение
; значение 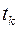 будем для простоты считать фиксированным.
будем для простоты считать фиксированным.
Прежде всего дискретизируем задачу, т.е. приближено значением непрерывную систему дискретно-непрерывной. Основания для этого следующее: во первых, дискретизация является неизбежным этапом подготовки задачи для ее решения на ЭВМ.
Во вторых, методику рассуждений проще пояснить на примере дискретно – непрерывной системы. Вообще говоря, основная сфера применения метода динамического программирования лежит в области дискретно-непрерывных либо чисто дискретных систем, либо систем, приближению к ним приводимых.
Разобьем интервал 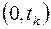 на
на  равных участков малой длины
равных участков малой длины 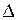 и будем рассматривать лишь дискретные значения
и будем рассматривать лишь дискретные значения 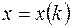 и
и 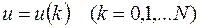 в моменты времени
в моменты времени 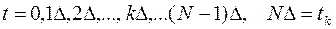 . Тогда дифференциальное уравнение (27) объекта можно приближенно заменить уравнением в конечных разностях
. Тогда дифференциальное уравнение (27) объекта можно приближенно заменить уравнением в конечных разностях


или 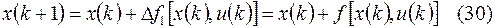 т.е.
т.е.
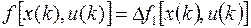
Начальное условие остается прежним
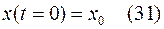
Интервал (28) приближенно заменяется суммой
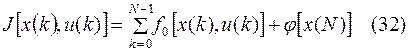
где 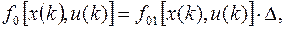
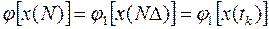
Задача теперь состоит в определении последовательности дискретных значений управляющего воздействия  , т.е. величины
, т.е. величины  , минимизирующих сумму (32) при условиях (4), (30) и (31), наложенных на систему таким образом, требуется найти минимум сложной функции многих переменных. Однако МДП дает возможность свести эту операцию к последовательности минимизаций значительно более простых функций одного переменного.
, минимизирующих сумму (32) при условиях (4), (30) и (31), наложенных на систему таким образом, требуется найти минимум сложной функции многих переменных. Однако МДП дает возможность свести эту операцию к последовательности минимизаций значительно более простых функций одного переменного.
Для решения задачи применяется прием, заключающийся в «понятном» движении о конца процесса, т.е. от момента 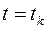 , к его началу. Допустим сначала, что рассматривается момент
, к его началу. Допустим сначала, что рассматривается момент 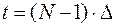 . Все значения
. Все значения 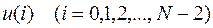 , кроме последнего
, кроме последнего 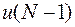 , уже каким то образом были осуществлены, причем получено некоторое значение
, уже каким то образом были осуществлены, причем получено некоторое значение 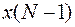 , соответствующие моменту
, соответствующие моменту 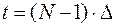 . Согласно принципу оптимальности воздействие
. Согласно принципу оптимальности воздействие 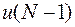 не зависит от «предыстории» системы и определяется лишь состоянием
не зависит от «предыстории» системы и определяется лишь состоянием 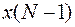 и целью управления.
и целью управления.
Рассмотрим последний участок траектории от 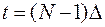 до
до 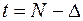 . Величина
. Величина 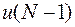 влияет лишь на те члены суммы (32), которые относятся к этому участку.
влияет лишь на те члены суммы (32), которые относятся к этому участку.
Обозначим сумму этих членов через  .
.
 из (30) получаем
из (30) получаем
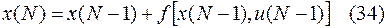
Следовательно, 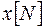 так же зависит от
так же зависит от 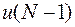 . Найдем допустимое значение
. Найдем допустимое значение 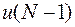 , удовлетворяющее (4) и минимизирующее величину
, удовлетворяющее (4) и минимизирующее величину  . Обозначим найденное минимальное значение
. Обозначим найденное минимальное значение  через
через 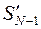 . Эта величина очевидно зависит от состояния системы при
. Эта величина очевидно зависит от состояния системы при 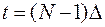 т.е. от значения
т.е. от значения 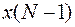 , входящее в (33) и (34). И так
, входящее в (33) и (34). И так 
Обратим внимание на то, что для определения  нужно проводить минимизацию только по одному переменному
нужно проводить минимизацию только по одному переменному 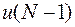 простого выражения (33)
простого выражения (33)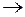 (вместо минимизации по многим переменным
(вместо минимизации по многим переменным 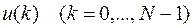 ) сложного выражения (32), выполнив этот процесс, получим
) сложного выражения (32), выполнив этот процесс, получим  в виде функций от
в виде функций от 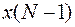 ; эту функцию следует запомнить, например, в каком либо запоминающем устройстве при вычислении на ЭВМ) при переходе к последующим стадиям решения.
; эту функцию следует запомнить, например, в каком либо запоминающем устройстве при вычислении на ЭВМ) при переходе к последующим стадиям решения.
Переедем теперь к предполагаемому участку времени. Рассматривая два участка – последний и предпоследний – вместе, можно заметить, что выбор 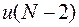 и
и 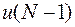 повлияет только на те слагаемые суммы (32), которые входят в состав выражения
повлияет только на те слагаемые суммы (32), которые входят в состав выражения
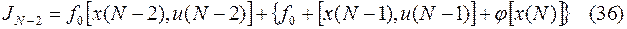
Величину 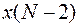 начальный момент последнего интервала полученную в результате «предыстории» процесса, будем считать. Из принципа оптимальности следует, что лишь значение
начальный момент последнего интервала полученную в результате «предыстории» процесса, будем считать. Из принципа оптимальности следует, что лишь значение 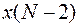 и цель управления – минимизация
и цель управления – минимизация  - определяют оптимальное управление на рассматриваемом участке времени.
- определяют оптимальное управление на рассматриваемом участке времени.
Найдем величину 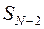 - минимум
- минимум  по
по 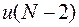 и
и 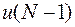 . Но минимум по
. Но минимум по 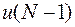 слагаемого, содержащегося в фигурной скобке выражения (36), уже был найден выше для каждого значения
слагаемого, содержащегося в фигурной скобке выражения (36), уже был найден выше для каждого значения 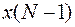 , а это последнее зависит от
, а это последнее зависит от 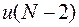 . Кроме того, при минимизации
. Кроме того, при минимизации  было попутно найдено и соответствующее оптимальное значение
было попутно найдено и соответствующее оптимальное значение 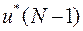 . Если учесть также, что первое слагаемое в (36) не зависит от
. Если учесть также, что первое слагаемое в (36) не зависит от 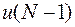 , то можно записать
, то можно записать
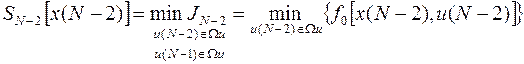
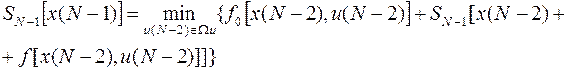
поскольку из (34)следует
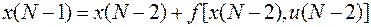
Отметим, что минимизация здесь производится также всего лишь по одному переменному 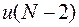 . При этом находим
. При этом находим  - оптимальное значение
- оптимальное значение 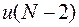 и величину
и величину 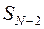 - минимум функционала
- минимум функционала  . Как
. Как  так и
так и 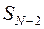 являются функционалами от
являются функционалами от 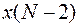 . Теперь можно поместить функцию
. Теперь можно поместить функцию 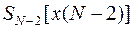 в ячейки блока памяти и стереть отныне не нужную функцию
в ячейки блока памяти и стереть отныне не нужную функцию 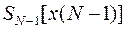 , находившуюся в блоке памяти раннее.
, находившуюся в блоке памяти раннее.
Важно отметить, что найденное оптимальное значение  . минимизируют все выражения в фигурной скобке формулы
. минимизируют все выражения в фигурной скобке формулы 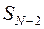 , а отнюдь не одно лишь слагаемое
, а отнюдь не одно лишь слагаемое 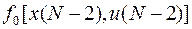 . Следовательно, стратегия, в которой каждое значение
. Следовательно, стратегия, в которой каждое значение  выбирается путем минимизации только лишь «своего» слагаемого
выбирается путем минимизации только лишь «своего» слагаемого 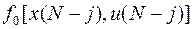 в сумме (32) вовсе не оптимальна. Она слишком «близорука», о чем уже упоминалось выше. Оптимальная стратегия учитывает конечную цель, т.е. минимизацию всего выражения в фигурной скобке, зависящего от
в сумме (32) вовсе не оптимальна. Она слишком «близорука», о чем уже упоминалось выше. Оптимальная стратегия учитывает конечную цель, т.е. минимизацию всего выражения в фигурной скобке, зависящего от  .
.
Можно продолжить описанную выше процедуру «понятного» движения от конца к началу промежутка 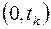 . Легко получить рекуррентную формулу
. Легко получить рекуррентную формулу

Параллельно в процессе минимизации правой части этой формулы определяется оптимальное значение
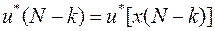 и минимизирующее выражение (37).
и минимизирующее выражение (37).
Вычисляя по формуле (37) последовательно 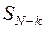 для
для 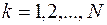 , приходим наконец, к определению оптимального значения
, приходим наконец, к определению оптимального значения 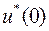 , требуемого в начальный момент времени.
, требуемого в начальный момент времени.
В некоторых простейших случаях удается провести всю описанную процедуру аналитически. Однако в общем случае аналитическое выражение результатов минимизации оказывается невозможным; поэтому данную процедуру можно рассматривать лишь как программу вычислений, производимых в простейших случаях вручную, а в более сложных на ЭВМ.
Весь процесс решения без затруднений переносится на объект любого порядка « » с уравнением (3) и любым числом управляющих воздействий
» с уравнением (3) и любым числом управляющих воздействий 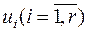 . Нужно лишь заменит скаляры
. Нужно лишь заменит скаляры 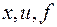 в приведенных выше формулах векторами
в приведенных выше формулах векторами  .
.
Выше изложенное может разочаровать тех читателей, которые представляли себе МДП неким волшебным рецептом для получения решений любых задач, причем эти решения мыслятся в виде готовых общих формул. Однако получит решение в таком виде большей частью невозможно, а иногда просто и ненужно. Обычно требуется решение в виде графиков и таблиц. Путь к получению этого решения, указанный выше, представляет собой процедуру вычислений для получения требуемой результата. Чем проще процедура вычислений, тем лучше метод. МДП отличается именно радикальным упрощением процедуры вычислений, ибо позволяет заменить минимизацию сложной функции по многим переменным последовательностью минимизаций по одной переменно гораздо менее сложных функций.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 857; Нарушение авторских прав?; Мы поможем в написании вашей работы!