Измерение больших радиусов кривизны сферических поверхностей с помощью зрительной трубы

Об

S П С ^¢

С

-z -f d f ^‘ z^’

Для измерения больших R применяется Автоколлимационные ЗТ. Если поместить вблизи Об. З.Т. с фокусным расстоянием f^/(на расст. d) исследуемую поверхность S, то автоколлимационное изображение С,^¢ являющееся изображением точки C, которая является центром радиуса R исследуемой поверхности. Используя обозначения, принятые в геометрической оптике, из формулы Ньютона zz^¢ = - f ^¢2 следует.

Для выпуклой поверхности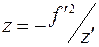

где: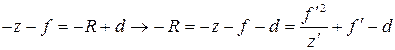

при f ^¢ >> d, R >> d, z^¢ = a₁ - a_{0 ,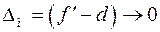} (4.9)

z^/ - измеряют как разницу между двумя установками: а₀ - положение автоколлимационного окуляра при установке ЗТ на ¥, для этого ставят плоское зеркало перед объективом ЗТ и находят положение заднего фокуса; а₁ - положение изображения точки С ^¢.

Для вогнутой поверхности аналогично предыдущему получим

z = R + (- f^’ - d) ® R = z + f + d

R = (- f^’2 / z ‘) - f’ +d ® R = - f’² / z’, где z’<0 (4.10)

Методическая погрешность измерения определится из (4.9), (4.10)

.

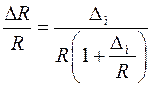Дифференцируя (4.9), (4.10) получим формулы для вычисления случайной погрешности

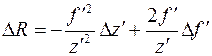
(4.11)

4.2.3. Интерференционный метод измерения радиусов кривизны сферических поверхностей (метод НЬЮТОНА)

Метод Ньютона применяется при R>1000 мм., где в качестве пробного стекла используют плоскопараллельную пластину.

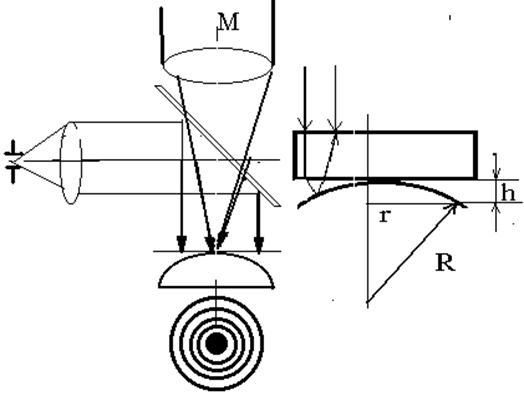
Из рисунка следует:

,

откуда

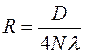, (4.12)

N- число темных интерференционных колец, ограниченных диаметром D N-го кольца. Для увеличения точности измерения R измеряют диаметры колец на периферии интерференционной картины с номерами i и j (j=i+N_i). Считая r_i,r_j радиусом i -го и j -го колец запишем аналогично предыдущему

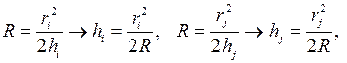
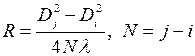(4.13)

Погрешность измерения ® 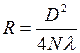1-ый способ (дифферинц.):

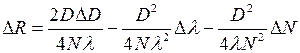(4.14)

2-ой способ

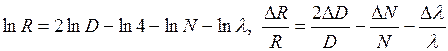
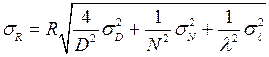(4.14)

Используя (4.13) определить s_R =? (самостоятельно)

ЛЕКЦИЯ 12

Дата добавления: 2014-01-11