Примеры. Пусть R – радиус шара, Р – любая точка на сфере, а во внутренней точке Р0 помещен единичный заряд

1. Функция Грина для шара

Пусть R – радиус шара, Р – любая точка на сфере, а во внутренней точке Р₀ помещен единичный заряд.

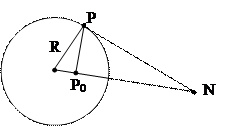На проводящей сфере индуцируется заряд, потенциал которого равен потенциалу некоторого точечного заряда, помещенного в инверсионном образе N точки Р₀, относительно сферы так, что выполнено равенство:

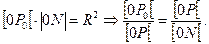
Треугольники ОРР₀ и ОРN подобны (общий угол и стороны пропорциональны).

Поэтому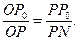

Пусть 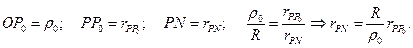Тогда

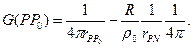(10)

Действительно, 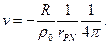Очевидно гармонична по Р в замкнутом шаре. Если же точка Р лежит на сфере, то

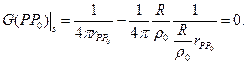
Как видно из (10) функция Грина для шара есть потенциал электростатического поля, созданный двумя точечными зарядами.

2. Функция Грина для полупространства

В качестве области ω берем часть, где 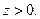Граница S имеет уравнение 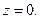В точке 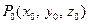помещаем единичный заряд, который создает поле с потенциалом .

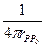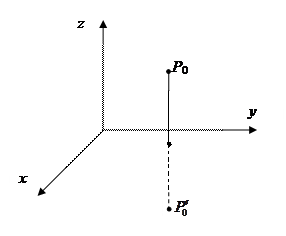Внесение проводящей поверхности 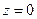приводит к индуцированию зарядов, потенциал которых можно заменить потенциалом отрицательного единичного заряда, помещенного в точку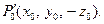

Суммарный потенциал

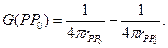
Рассмотрим задачу Дирихле для полупространства .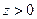

.

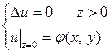Ее решение:

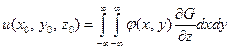
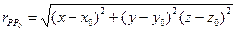
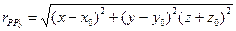
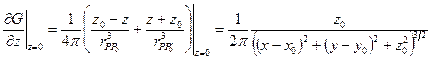
или

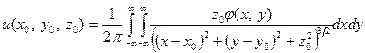
3) Функции Грина для полушара.

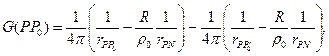
где

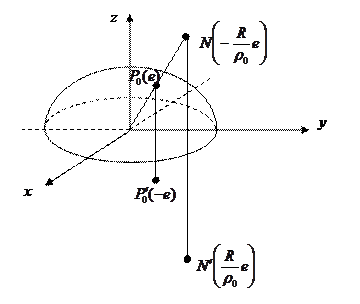
Тема 6. Метод Фурье.

Лекция 1. Разделение переменных.

Рассматриваемые вопросы.

1. Решение основных краевых задач методом Фурье.

2. Интеграл Пуассона.

3. Внешняя и внутренняя задачи Дирихле.

Пусть ω – круг радиуса R с центром в начале координат, а S – окружность (граница области ω.

Рассмотрим задачу Дирихле

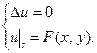(1)

Перейдем к полярным координатам по формулам

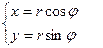
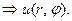
Оператор Лапласа в полярных координатах

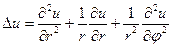
и задача (1) эквивалентна задаче

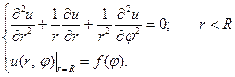(2)

Будем искать решение 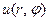в виде:

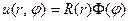
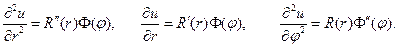
Подставим в уравнение Лапласа

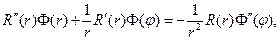
или

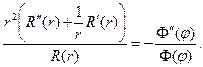
Следовательно, и левая и правая части этого равенства суть const (можно показать, что эта постоянная положительна)

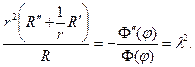
Угловая функция Ф(φ) должна быть периодической. Учитывая это, получим задачу Штурма-Лиувилля.

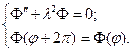(3)

Равенство (3) возможно лишь в случае

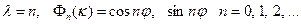
Для искомой функции R(r) получаем уравнение

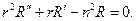
Будем искать решение этого уравнения в виде 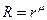, тогда

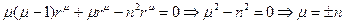
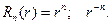
Если же n =0, то 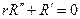. Как нетрудно проверить имеет своими решениями 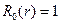и ln r. Таким образом, мы получаем набор функций, гармонических в круге

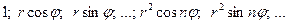
Если предположить, что ряд

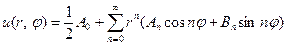(4)

можно дифференцировать почленно, то его сумма 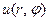также будет гармонической функцией.

Подберем коэффициенты этого ряда так, чтобы

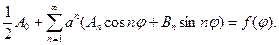
Отсюда с учетом формул для коэффициентов Фурье следует:

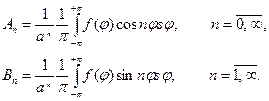
Замечание. Ряд (4) очевидно дает общий вид гармонической функции для круга r<a. Угловые функци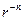и и 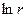при этом не использовались, так как они при 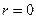разрывны. Вместе с тем, если рассматривать область r>a (внешняя сторона круга), то общий вид гармонической функции для этой области будет задаваться рядом:

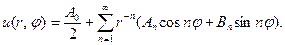(5)

И, наконец, для кольца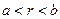

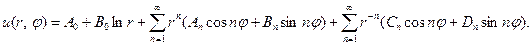(6)

Преобразуем теперь найденные решения к более удобному представлению

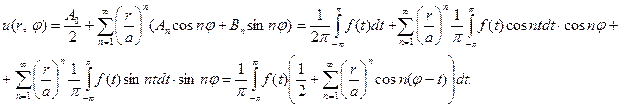
Перестановка операций суммирования и интегрирования законна, так как ряд

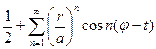
сходится равномерно по φ и t нутрии круга r<a. Найдем сумму этого ряда

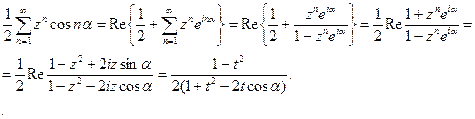
Поэтому

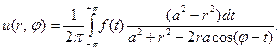(7)

Представление (7) известно как интеграл Пуассона.

Замечание. Среди двумерных областей, для которых задача Дирихле для уравнений Лапласа решается эффективно методом разделения переменных в декартовых координатах, можно отметить прямоугольник со сторонами параллельными осям координат и в, частности, полуполосу.

Тема 7. Теория потенциала.

Лекция 1. Теория потенциала.

Рассматриваемые вопросы.

1.Объемный и логарифмический потенциалы.

2. Поверхностные потенциалы.

3. Решение основных краевых задач методом потенциала.

Некоторые сведения из теории потенциала.

1. Объемный потенциал и его свойства.

Предположим, что в области 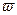распределен электрический заряд с плотностью 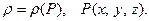Для нахождения потенциала такого электростатического поля разобьем область ω на элементарные части 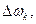не имеющие общих внутренних точек. Допустим, что действие заряженной области 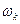равносильно действию точечного заряда 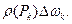Тогда потенциал электростатического поля в точке наблюдения 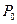можно найти по формуле:

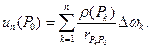
При 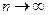очевидно

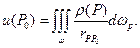(1)

Функцию (1) называют объмным или ньютоновским потенциалом.

Свойство 1. Объемный потенциал есть гармоническая функция по координатам точки 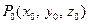во внешней области .

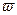Если 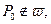то (1) есть обычный тройной интеграл, функция 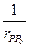имеет непрерывные производные любого порядка, интеграл 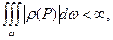поэтому производные по 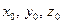можно вычислять дифференцированием под знаком интеграла. В частности

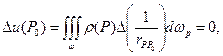
так как 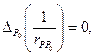если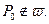

Свойство 2. Объемный потенциал есть непрерывная функция по координатам точки 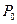во всем пространстве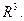

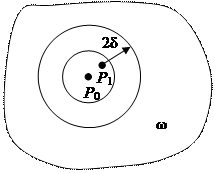
Действительно, непрерывности в внешности 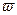вытекает из ее гармоничности. Пусть теперь точк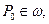а а 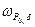есть шар радиуса 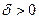с центром в точке 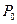такой, что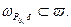

Рассмотрим разность 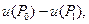где точка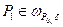

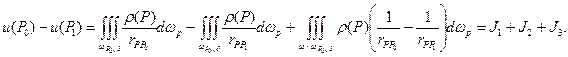
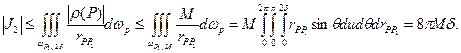
Для 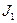аналогично получаем

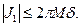
Будем считать, что δ фиксировано так, что

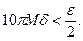
Оценим теперь 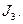Если 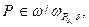то выбирая Р ₁ достаточно близко к Р ₀ получим

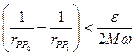
с помощью которого

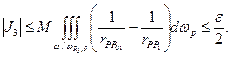
А значит

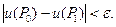
Непрерывность во внутренних точках области ω объемного потенциала доказана.

Пусть теперь точка 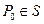– границе области ω. Рассмотрим более широкую область 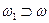и положим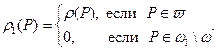

Тогда

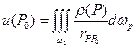
и точка Р ₀ будет внутренней по отношению к 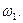Следовательно, потенциал в точке Р ₀ непрерывен.

Свойство 3. Объемный потенциал имеет непрерывные производные первого порядка в 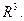Доказательство аналогично доказательству свойства 2.

Свойство 4. Если плотность 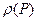имеет непрерывные производные первого порядка, то объемный потенциал имеет производные второго порядка в области ω и удовлетворяет уравнению Пуассона

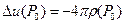
(без доказательства).

Замечание 1. С помощью объемного потенциала решение задачи Дирихле для уравнения Пуассона может быть сведено к решению задачи Дирихле для уравнения Лапласа.

Замечание 2. В двумерном случае роль объемного потенциала играет так называемый логарифмический потенциал

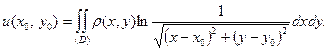
Поверхностные интегралы простого и двойного слоя.

Пусть на некоторой достаточно гладкой поверхности S распределен заряд с плотностью 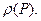Тогда потенциал электростатического поля в точке 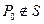представляется в виде:

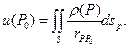(2)

Функцию (2) называют потенциалом простого слоя. Перечислим некоторые свойства этого потенциала.

1). Потенциал простого слоя есть гармоническая вне S функция.

2). Потенциал простого слоя есть непрерывная во всем пространстве 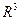функция.

3). Нормальная производная потенциала простого слоя терпит разрыв при переходе через поверхность S.

Потенциалом двойного слоя называется выражение

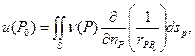
где ν(Р) – есть плотность распределения дипольного момента, а 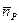– внутренняя нормаль к S.

4). Потенциал двойного слоя есть гармоническая вне S функция.

5). Потенциал двойного слоя терпит разрыв при переходе через поверхность S.

6). Потенциал двойного слоя может быть представлен в виде:

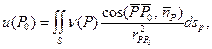
Аналогично могут быть введены криволинейные интегралы простого и двойного слоя с аналогичными свойствами.

Замечание. С помощью потенциала двойного слоя решение задачи Дирихле можно свести к решению уравнения Фредгольма второго рода относительно неизвестной функции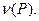

Дата добавления: 2014-01-11