Представление чисел

Представление данных в электронных вычислительных машинах

Машинные элементы информации

Информация, вводимая в ЭВМ, должна быть представлена исключительно в двоично-кодированной форме. В ЭВМ вводится информация двух типов: управляющая вычислительным процессом (программы) и исходные данные (обрабатываемая информация). И та и другая кодируются в двоичном виде.

В общем случае для кодирования дискретной величины, принимающей N различных значений, требуется n двоичных разрядов, n=log₂N, (2ⁿ=N): а₁,а₂, …,а_n. Каждому двоичному разряду a_i двоичного кода a_1,a_{2, …,} a_n соответствует единица информации, называемая битом. Бит - это двоичный разряд (двоичная цифра) в двоичном коде. Двоичный код длиной 8 разрядов (n=8) называется байтом (В-обозначение байта). Из байтов обычно строятся более крупные единицы информации - слова. В ЭВМ различных типов длина слов различна: n=16,24,32,…Более крупные единицы информации - двойные слова (например, в IBM PC двойные слова состоят из 4 байтов), учетверенные слова (в IBM PC учетверенные слова состоят из 8 байтов).

Биты, байты, слова, двойные слова имеют фиксированную длину и относятся к так называемым машинным элементам информации фиксированного размера. Такого рода машинные элементы информации используются в ЭВМ как для представления данных, так и для представления команд, адресов операндов.

Кроме машинных элементов фиксированной длины в ЭВМ используются и другие машинные элементы - переменной длины. В PC - это строка байтов, длина которой ограничена только размерами ОП и в пределе может достигать 2³²В=4ГВ (от 1В до 2³²В). В ЭВМ типа IBM 370 это поле переменной длины от 1 до 255 В. Сторока байтов как машинный элемент может использоваться для представления различных типов данных: строк текста, двоично-десятичных чисел и т.п.

Машинные элементы IBM PC: байт, слово – два байта (n=16), двойное слово (n=32), учетверенное слово (n=64), а также строка байтов.

В ЭВМ на машинном уровне, т.е. в АЛУ, обеспечивается обработка данных трех типов (только!): чисел, символов, логических значений. Адреса (номера ячеек памяти) представляются целыми числами. Данные других типов (т.е. имеющие более сложную структуру)на уровне аппаратуры не обрабатываются. Как быть? Они обрабатываются на программных уровнях путем выполнения команд, в которых используются возможности АЛУ по обработке данных только трех типов.

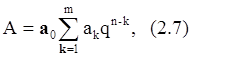В общем виде число А в позиционной системе счисления можно представить:

где a_kÎ{0,1,….q-1}, q – основание системы счисления, обычно принимает значения q=2(8,10,16), a₀ - знак числа, a_k - цифры числа, q^n-k - вес цифры в зависимости от ее позиции, n - количество цифр в целой части числа, m - общее количество цифр.

Пример: А=217,37 – десятичное число, q=10, n=3, m=5.

Все основное множество чисел можно разделить на два подмножества - целые и вещественные (действительные). Основной формой представления чисел в ЭВМ являются двоичные числа.

Целые двоичные числа в ЭВМ представлены в следующем формате:

Веса: 2^k 2^k-1 … 2¹ 2⁰.

Диапазон представления: ±(2^k-1). Основная особенность - переполнение разрядной сетки при выполнении операций сложения, вычитания, умножения и деления, если результат операции С удовлетворяет условию |С|³2^k. Как обнаружить? Например, при сложении переполнение возможно, если знаки слагаемых одинаковы. В результате переполнения знак суммы изменяется и не совпадает со знаком слагаемых. Технически в ЭВМ переполнение обнаруживается путем анализа битов переноса в знаковый разряд сумматора p₁ и из знакового разряда p₀: условие переполнения - p₀ ¹ p_1.

Пример: +5+(+4)=-1, (k=3).

p0	p1	Å

Сигнал переполнения формируется схемой сложения Å по mod 2

В ЭВМ IBM PC для представления целых чисел можно использовать целые без знака разрядности k=8,16,32,64 и целые со знаком разрядности k=7,15,31,63, т.е. для представления целых можно использовать байт, слово, двойное слово, учетверенное слово. Для представления действительных чисел можно использовать два способа: правильная дробь или плавающая запятая (формат чисел с плавающей запятой).

Двоичная правильная дробь имеет формат:

2⁰ 2^-1 2^-k

Диапазон представления: ±(1-2^-k). Наименьшее число, отличное от нуля, - 2^-k=0,0…01. Числа, меньшие чем 2^-k, рассматриваются как машинный ноль. Таким образом, если целые числа в ЭВМ представлены точно (без погрешности), то действительные числа с дискретностью 2^-k=D. Т.е. разрядность числа k определяет точность представления действительных чисел в k-разрядной сетке. D=2^-k - это дискретность, с которой идет «прореживание» множества действительных чисел в k-разрядной сетке.

-1 +1

Пример: k=15, D=2^-15»0,3×10^-4, т.е. точность представления приблизительно три десятичных знака.

Особенности операций над правильными дробями: переполнение разрядной сетки при выполнении операций сложения, вычитания и деления. Условие переполнения |С|³1=2⁰, переполнение разрядной сетки при выполнении операции умножения не происходит. Общая для двух форматов с фиксированной запятой - для целых чисел и для правильной дроби особенность: представление отрицательных чисел не в прямом коде (как для положительных чисел), а в дополнительном (или обратном) коде.

Дополнительный код используется для представления отрицательных чисел. Для чего? Для того, чтобы с помощью двоичного комбинационного сумматора стало возможным складывать не только числа без знаков, но и числа с отрицательными знаками.

Пример: +4+(+3)=+7(0.111), -4+(-3)=1.100+1.011=0.111(+7)? При сложении чисел с отрицательными знаками сумматор дает неправильный результат. Для того, чтобы знаки чисел стало возможным обрабатывать так же, как цифры числа, и вводится дополнительный 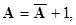код. Дополнительный код определяется выражением:

где А - цифровая часть числа (без знака).

Примеры: -4 = 1.100_пр = 1.100_д.к, -3 = 1.011_пр = 1.101_д.к.

Сложение: 1.100+1.101=1.001_д.к=1.111_пр=-7.

Двоичные числа с плавающей запятой -универсальный формат, который можно использовать для представления любых чисел – целых, правильных дробей и неправильных дробей в широком диапазоне. Для представления двоичного числа с плавающей запятой используется формула: А=±М×d^±P, (2.8)

где d=2^h, (h=1или 4) - основание системы счисления с плавающей запятой, M – мантисса ( формат представления - правильная дробь), P - порядок числа ( формат представления - целое число). Формат числа с плавающей запятой:

Здесь: М – мантисса числа, Р - порядок числа, m₀ – знак числа_, p₀ – знак порядка.

Диапазон представления (если мантисса нормализована):

d^-1 d^-Pmax£ |A| £ (1-2^-n)d^+Pmax (2.9)

Здесь: P_max = (2^k-1) – максимальный порядок числа.

Диапазон представления на числовой оси:

В IBM PC для представления действительных чисел можно использовать три формата: с одинарной, двойной и расширенной точностью:

Здесь: М – мантисса, Х =Р+2^(k-1)–1 - характеристика порядка числа, k=8,11,15; m=23,52,64 бита. Другими словами, для представления действительных чисел можно использовать 4, 8 или 10 байтов. Один формат от другого отличается длиной мантиссы и, следовательно, дискретностью (точностью) представления чисел: D=2^-23(-52,-64)

Особенности представления действительных чисел в IBM PC.

1. Мантисса М - неправильная дробь:

m₀=1 (const) - у нормализованной мантиссы старший разряд всегда равен 1, поэтому в памяти ее можно не хранить и тем самым сэкономить один бит памяти. При извлечении из памяти эта единица восстанавливается по умолчанию и мантисса становится 24-разрядной (или 53-разрядной – с двойной точностью).

Вторая особенность - вместо порядка P используется характеристика Х:

X=P+2^k-1-1=P+127(1023, 16383).

Характеристика - целое без знака (в отличие от порядка), что обеспечивает упрощение операций над порядками.

Третья особенность - дополнительный код в формате с плавающей запятой не используется, а используется обратный код, поэтому ноль имеет две формы – плюс ноль: 0.0…0 и минус ноль:1.1...1.

Операции с плавающей запятой выполняются в специальном АЛУ с плавающей арифметикой (в сопроцессоре).

Двоично-десятичные числа (ВСD) -можно использовать для представления десятичных чисел. Суть: каждой десятичной цифре 0,1, …, 9 ставится в соответствие двоичный код 0000, …, 1001.

В PC для представления двоично-десятичного числа можно использовать три формата: упакованный и не упакованный форматы произвольной длины (машинный элемент - строка байтов), а также упакованный формат фиксированной длины в 10 байтов(18 десятичных цифр).

Упакованный формат: один байт содержит две десятичных цифры (по 4 бита каждая).

Не упакованный формат: один байт - одна десятичная цифра (4 бита из 8 не используются). Количество байтов зависит от количества десятичных цифр и формата числа.

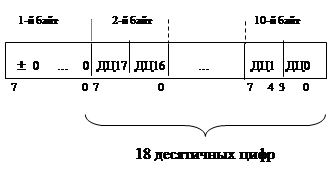Третий формат содержит 80 двоичных разрядов (10 байтов):

Операции над числами типа ВСD выполняются в сопроцессоре.

Дата добавления: 2014-01-11