Функция и структура операционного автомата

Функция ОА считается заданной, если заданы (определены) три множества S,Y,X:

- S=DÈRÈI - множество слов, где D - множество входных слов ОА (в МП умножения - это два слова А и В); R - множество выходных слов-результатов (в нашем примере это слово С); I - множество внутренних слов (в примере с умножением это слово СЦ).

- Y={y₁,..., y_m} - множество (список) микроопераций (в примере с умножением - это y₁,..., y₇).

- X={x₁,..., x_L} - множество (список) ЛУ (в примере это x₁, x₂,x₃).

Объединение производится по всем операциям ОУ:

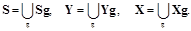В общем случае МО описывается выражением y_m: S_i:=j_m(S_j, S_n). Здесь: j_m - некоторая вычислимая функция (например, сумма), S_i, S_n - её аргументы, S_{i -} значение функции j_m, вычисленное при заданных значениях аргументов S_j = S_j^*, S_n = S_n^* (например: S_j^* = 5, S_j^* = 10, S_j= 5+10=15).

В общем случае ЛУ описывается выражением: x_l:=j_l (S_j), где j_L - булева функция, S_j - аргумент функции j_l, x_l - её значение при S_j=Sj^*.

Пример: х₂ = 1, если СЦ = 0, или х₂ = 1,если СЦ ¹ 0.

Набор ЛУ X={x₁, …, x_L} отображает состояние ОА.

Следует отметить, что время не является аргументом функции ОА. Это означает, что функции ОА устанавливают только список действий Y и формируемых осведомительных сигналов X. Порядок выполнения МО и формируемых ЛУ в функциях ОА не указывается, отсутствует. Это означает, что функции ОА характеризуют только те средства, которые могут быть использованы для обработки информации, но не сам вычислительный процесс. Порядок выполнения МО - вычислительный процесс (динамику) задают микропрограммы операций множества F: МП₁, …, МП_G, реализуемые УА (совместно с ОА, разумеется). Следовательно, совокупность микропрограмм МП₁, …, МП_G задает функцию УА. Функция УА задана, если заданы (описаны, выбраны, разработаны) МП всех операций F={f₁, …,f_G}. Организацию УА рассмотрим позже. Алгоритмы выполнения операций в ОУ обычно задаются в форме граф-схем алгоритмов (ГСА). Именно ГСА (микропрограмма) задает вычислительный процесс во временном аспекте, как последовательность действий (шагов), ведущая к результату.

Определив функцию ОА, можно переходить к его структуре. Сначала продолжим пример с умножением. Для реализации умножения ОА должен выполнять следующие функции:

1) S_умн = А(0:15), В(0:15), С(0:15), СЦ(1:4)

2) Y_умн - y₁:С:=0; y₂: СЦ:=15; y₃: С:=С+А; y₄: С.В:=SHR1(0.С.В);
y₅: СЦ:=СЦ-1; y₆: С:=С+1; y₇:С(0):=А(0)ÅВ(15);

3) X_умн - x₁:В(15); x₂:СЦ=0; x₃:В(0).

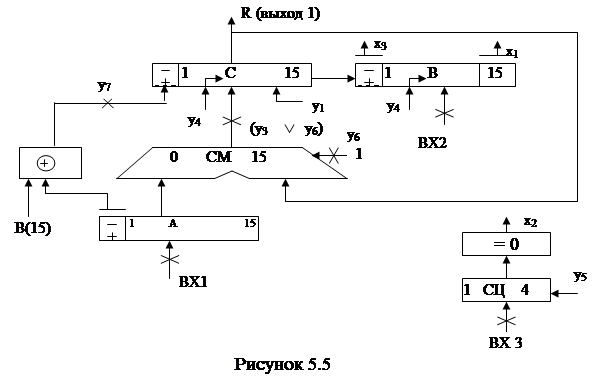Cтруктура ОА для операции умножения представлена на рисунке 5.5.

В общем случае структура ОА имеет вид, представленный на рисунке 5.6. ОА состоит из трех составных частей:

S - память ОА (для хранения слов S=S₁, …,S_N),

Ф - множество (набор) комбинационных схем для реализации МО,

y - набор КС для формирования осведомительных сигналов.

Дата добавления: 2014-01-11