Прямокутні аксонометричні проекції

Лекция

Роль институтов в обществе. Функции и значение института.

Понятие института. Роль институтов в функционировании экономики.

5).

4).

3).

2).

1).

Правило Крамера

3)

2)

2).

_{(4,0) )}

_{((2,0) )}

_{(0,-3) )}

_{(0,-3/2) )}

Х₁

₀

Х₂

3).

_{(6,0) )}

_{(0,-2) )}

Х₁

₀

Х₂

- загальний розв’язок системи

Розглянемо систему лінійних алгебраїчних рівнянь 3-го порядку (з трьома невідомими) вигляду:

(1.8)

Матриця А – основна матриця системи (1.8)

Означення 2. Визначником 3-го порядку основної матриці системи (1.8) називається

(1.9)

Система (1.8) зводиться до наступного вигляду:

(1.10)

де визначники,, одержуються

Проаналізуємо можливі розв'язки:

1)

Х₁

Х₂₂

Х₃

ПРАВИЛО САРРІУСА (САРРЮСА) обчислення визначника 3-го порядку

+ a₁₂a₂₃a₃₁

+ a₁₁a₂₂a₃₃

+ a₁₃a₂₁a₃₂

a₂₃

a₂₂

a₂₁

a₃₃

a₃₂

a₃₁

a₃₁

a₁₁

a₁₂

a₁₃

a₂₁

a₂₂

a₂₃

a₃₂

a₃₃

- a₁₂a₂₁a₃₃

- a₁₃a₂₂a₃₁

- a₁₁a₂₃a₃₂

a₁₁

a₁₂

a₁₃

Приклад

Означення 3. Перестановки:

Означення 4. Інверсії (невпорядкованість)

число інверсій у перестановці з п чисел

Приклад6 знайти число інверсій у перестановці з 7 чисел:

Будова визначників 2-го і 3-го порядків

Означення 3. Визначником п-го порядку називається

Розглянемо систему лінійних алгебраїчних рівнянь п-го порядку

(1.11)

КРАМЕР ГАБРІЕЛЬ (31.07.1704 - 4.01.1752)

(1.12)

(1.13)

Найкращий спосіб вивчити що-небудь - це відкрити самому Д.Пойа

Означення 4. Транспонування – це

ВЛАСТИВОСТІ ВИЗНАЧНИКІВ

1р.х(-4)+2р.; 1р.х(-7)+3р.

МІНОРИ ТА АЛГЕБРАЇЧНІ ДОПОВНЕННЯ ЕЛЕМЕНТІВ ВИЗНАЧНИКА

Означення 5.

ТЕОРЕМА ЛАПЛАСА П”ЄРА СІМОНА

(23.03.1747 – 5.03.1827)

1=). 2 ст.-4ст., 4ст.х2 + 3ст.

2=). Розкладаємо визначник за елементами 3-го рядка

5=). 1стх3+2ст., 1 ст.х(-3)+3 ст.

6=). Розкладаємо визначник за елементами 2-го рядка

Обчислити визначник 4-го порядку:

=

to institute (англ) - устанавливать, учреждать.

Под институтами мы будем понимать публичную систему правил, которые определяют должность и положение с соответствующими правами и обязанностями, властью и неприкосновенностью, и т.п. Эти правила специфицируют определенные формы действий в качестве разрешенных, а другие в качестве запрещенных, и по ним же наказывают одни действия и защищают другие, когда происходит насилие. В качестве примеров, или более общих социальных практик, мы можем привести игры, ритуалы, суды и парламенты, рынки и системы собственности.

В экономической теории впервые понятие института было включено в анализ Торстейном Вебленом:

- привычные способы реагирования на стимулы;

- структура производственного или экономического механизма;

- принятая в настоящее время система общественной жизни.

Джон Коммонс: Институт – коллективное действие по контролю, освобождению и расширению индивидуального действия.

Уэсли Митчелл: Институты – господствующие, и в высшей степени стандартизированные, общественные привычки.

В настоящее время в рамках современного институционализма наиболее распространенной является трактовка Дугласа Норта:

Институты - это правила, механизмы, обеспечивающие их выполнение, и нормы поведения, которые структурируют повторяющиеся взаимодействия между людьми.

Чтобы избежать согласования множества внешних факторов, влияющих на успех и на саму возможность принятия того или иного решения, в рамках экономического и социального порядков вырабатываются схемы или алгоритмы поведения, являющегося при данных условиях наиболее эффективным. Эти схемы и алгоритмы или матрицы поведения индивидов есть ни что иное, как институты.

Таким образом:

1. Институты определяются как «правила игры», которые определяют поведение организаций и индивидов в экономике;

2. Институты определяются как культурные нормы, вера, менталитет.

3. Институты определяются как организационные структуры, например, финансовые институты: банки, кредитные учреждения.

4. Понятие институт может использоваться применительно к личности или к определенному посту (например, институт президентства).

5. Теоретико-игровой подход: институты как равновесие в игре.

Институты и организации. Институты – правила игры, организации – игроки.

К. Менар: «Организация – это экономическая единица координации, обладающая доступными определению границами и функционирующая более или менее непрерывно для достижения определенной цели или совокупности целей, разделяемых членами-участниками». Для организации характерны:

1. совокупность участников;

2. согласие или несогласие, подразумеваемое, или открыто выраженное относительно целей и средств организации (контракты, увольнение, забастовки);

3. формальная координация, определяющая структуру с учетом степени ее сложности (иерархия) правил и процедур (формализацией) и степени централизации принятия решений.

Скоробогатов: В качестве наиболее общего определения института можно предложить следующее: институт — это любой механизм, обеспечивающий координацию и/или эффективную мотивацию экономического поведения.

Значения термина «институт» в неоинституциональной теории.

В институциональной теории можно выделить несколько значений термина институт, различающихся как по широте охвата экономических явлений, так и по смыслу.

Институты создаются людьми, чтобы обеспечить порядок и сократить неопределенность обмена. Они обеспечивают предсказуемость поведения людей. Институты позволяют экономить наши мыслительные способности, так как, выучив правила, мы можем приспособиться к внешней среде, не пытаясь ее осмыслить и понять.

.

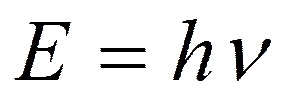
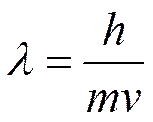(1)

В 1926 г. австрийский физик Э. Шредингер нашел математическое выражение, описывающее поведение волн материи – уравнение Шредингера:

.

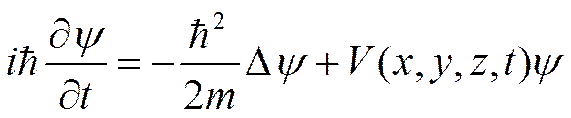(Здесь ψ – волновая функция частицы, m, v – ее масса и скорость, x,y,z -- координаты, V – потенциал, Δ – оператор Лапласа).

Вселенная означает весь существующий материальный мир, понятие метагалактика означает этот же мир с точки зрения его структуры.

Магеллановы облака. Ближайшая к нам галактика

Реконструкция нашей галактики

Классическая ньютонова космология явно или неявно принимала следующие постулаты:

1. Вселенная – всесуществующий «мир в целом». Космология познает мир таким, каким он существует сам по себе, безотносительно к условиям познания.

2. Пространство и время Вселенной абсолютны, они не зависят от материальных объектов и процессов.

3. Пространство и время метрически бесконечны.

4. Пространство и время однородны и изотропны.

5. Вселенная стационарна, не претерпевает эволюции. Изменяться могут конкретные космологические системы, но не Мир в целом.

В ньютоновой космологии возникли два парадокса, связанные с постулатом о бесконечности Вселенной.

1. Гравитационный парадокс. Если Вселенная бесконечна, то в ней существует бесконечное число небесных тел, которые должны создать бесконечно большое гравитационное притяжение и Вселенная должна сколлапсировать – собраться в точку.

2. Бесконечное число светящихся звезд должно привести к бесконечно большой светимости небосвода. Парадокс получил название фотометрического.

Первые модели Вселенной использовали теорию тяготения А. Эйнштейна. Уравнение Эйнштейна допускает несколько решений, т.е. существует несколько моделей Вселенной.

В) У множества моделей Вселенной есть несколько общих моментов:

1) Наша Вселенная расширяется и эволюционирует.

2) Радиус Вселенной в сингулярности составлял не более 10^-14 м, т.е. меньше радиуса электрона, и ее плотность составляла 10⁹⁶ г/см³.

3) От первоначального состояния к настоящему Вселенная пришла в результате Большого взрыва.

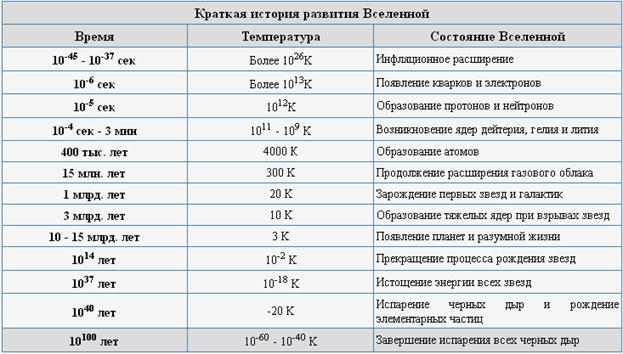
В результате своей эволюции Вселенная прошла ряд этапов, которые принято называть эрами.

Эра адронов. Продолжительность эры 10^-3 с, температура 10¹² К, плотность 10¹⁴ г/см³. В конце эры происходит нарушение хиральной симметрии и аннигиляция частиц и античастиц приводит к победе вещества над антивеществом в итоге остается некоторое количество протонов, гиперонов и мезонов.

Эра лептонов. Продолжительность 10 с, температура 10¹⁰ К, плотность 10⁴ г/см³. Возникает электромагнитное взаимодействие. Протоны распадаются на нейтроны и позитроны. Аннигиляция частиц и античастиц привела к появлению фотонов, столкновения которых приводит к рождению пар электрон-позитрон.

Фотонная эра. Продолжительность 10⁶ лет. Температура падает от 10¹⁰ К до 3000 К. Плотность от 10⁴ г/см³ до 10^-21 г / см³. Появляются ядра атомов гелия. Свет отделяется от вещества, и Вселенная становится прозрачной, в ней определяющую и структурирующую роль начинает играть гравитационное взаимодействие.

Звездная эра. Она начинается через 10⁶ лет от начала взрыва и продолжается сейчас. В первые этапы появляются протозвезды и протогалактики. В звездах начинается синтез гелия. «Выгорание» водорода приводит к гравитационному сжатию звезд, их разогреву и последующему взрыву. Во время взрыва протозвезд рождаются все химические элементы после чего и рождаются звезды нового поколения. (Солнце звезда второго поколения.) Вся история Вселенной длится (14±2)^.10⁹ лет.

Иерархия – расположение частей, элементов от низшего к высшему или от высшего к низшему; порядок подчинения низших высшим.

Тождество – полное сходство, совпадение; равенство, справедливое при любых числовых значениях входящих в него величин.

Структура – строение, внутреннее устройство.

Вселенная – весь существующий материальный мир бесконечно разнообразный по формам, которые принимает материя в процессе ее развития.

Галактика – гигантское скопление звезд, объединенных гравитационным взаимодействием.

Метагалактика – часть Вселенной, доступная астрономическим исследованиям.

Энергия связи – работа, которую необходимо затратить, чтобы «растащить» объект на составные части.

Тождественные частицы – частицы, обладающие одинаковыми физическими свойствами: массой, спином, электрическим зарядом и другими внутренними характеристиками. Принципиальная неразличимость частиц чисто квантовомеханическое свойство.

Все многообразие мира, все его иерархические структуры объясняют четыре типа взаимодействия между микрочастицами, составляющие микро-, макро- и мега- миры. Это гравитационное, электромагнитное, слабое и сильное взаимодействия.

Первое объединение различных физических теорий принято считать уравнения Максвелла, объединивших единым описанием электрические, магнитные и оптические явления.

На следующем этапе развития А. Эйнштейну удалось объединить электромагнитное и гравитационное взаимодействия в общей теории относительности.

Дальнейшее объединение гравитационного и электромагнитного взаимодействий в электрослабое взаимодействие происходит в 70-е годы ХХ. Экспериментальное подтверждение электрослабого взаимодействия было получено в 1983 г. (открытие векторных бозонов).

Дальнейшее объединение взаимодействий называют единой теорией поля.

Единая теория поля – единая теория материи – это теория, призванная свести все многообразие свойств элементарных частиц и их взаимодействия (взаимопревращений) к небольшому числу универсальных принципов. Такая теория еще не построена, и ее нужно рассматривать, как стратегию развития физики микромира. В настоящее время в рамках единой теории поля существует довольно много частных моделей.

Важным предсказанием различных моделей великого объединения считают предсказание нестабильности протона (время жизни 10³⁰ – 10³⁴ лет).

Перспективной считается модель суперструн. Теория требует многомерного (26 или 10-мерного) пространства. На этом пути возможно построение теории, содержащую все взаимодействия всех известных фундаментальных частиц. Однако теория предсказывает наличие пока не обнаруженных частиц с большой массой (>1 ТэВ).

Прямокутна ізометрія. Кут між осями в ізометрії – 120^о (рис.4.1). Коефіцієнт спотворення по осях х, у, z рівний 0,82; як правило, його округляють до 1. Кола, що лежать в площинах, паралельних площинам проекцій, проектуються на ці площини в еліпси. Великі осі еліпсів на П₁, П₂, П₃ перпендикулярні відповідно до осей z, у, х. Якщо коефіцієнт спотворення по осях прийняти рівним 1, то великі осі еліпсів рівні 1,22, а малі - 0,71 від діаметра кола.

В аксонометричних проекціях кола проекціюються на основні площини у вигляді еліпсів, які зручно замінити овалами.

На рис. 4.2. наведено спрощену побудову овалів за заданим діаметром кола при різному його положенні відносно площин проекцій.

Овал будують наступним чином: з центру О₁ проводять прямі паралельні до двох аксонометричних осей, в яких знаходиться коло; з точки О₁ проводимо велику вісь овалу, яка в площині кресленика перпендикулярна до третьої аксонометричної осі, а перпендикулярно великій осі проводимо малу вісь;будуємо коло заданого діаметру D та відмічаємо точки перетину кола з осями – точки О₂ і О₃, m i m₁; з точок О₂ і О₃ проводимо дуги mm і m₁m₁ радіусами R=O₂m=O₃m₁; сполучаємо точку О₃ з точками m₁ та з точок перетину О₄ і О₅ проводять дуги r=O₄m=O₅m.

Прямокутна диметрія. Розміщення осей в прямокутній симетрії показано на рис. 4.3. коефіцієнти спотворення по осі у = 0.47, а по осі х і z k = 0.94. Але, як правило, симетричну проекцію виконують без спотворення по осях х і z, тобто коефіцієнти спотворення по цих осях приймають рівними одиниці, а по осі у коефіцієнт спотворення 0.5. Якщо коефіцієнт спотворення по осях х і у взятий рівним 1, то великі осі еліпсів рівні 1,06 від діаметра кола, мала вісь еліпса на П₂ рівна 0,95, а еліпсів на П₁ і П₃ - 0,35 від діаметра кола.

Побудова еліпсів в диметрії, як і в ізометрії, також замінюється овалами (рис. 4.4).

Розглянемо побудову овалу, паралельного до горизонтальної площини проекцій (хоу). Порядок побудови: визначаємо положення центра О₁, через нього проводять прямі паралельні аксонометричним осям і велику ось овалу, перпендикулярну осі z; з центру овалу проводять кола заданого діаметру D, яка відмічає на осі, паралельній до ох, точки n і n₁; з центру О₁ вздовж осі оz відкладаємо відрізки рівні діаметру О₁О₂ = О₁О₃ = D; з точок О₂ і О₃ радіусами R₁ = О₂n₁ = О₃n проводять дуги nn i n₁n₁ до перетином з колом діаметром D; з’єднуючи точки О₂ і О₃ з точками n і n₁ на перетині з великою віссю, отримують точки О₄ і О₅, з яких радіусом r = О₄n = О₅n проводять дуги, що замикають овал.

Овал паралельний до фронтальної площини проекцій (хоz) будують наступним чином: визначають положення центру овалу, через який проводять прямі паралельні аксонометричним осям, і велику вісь овалу перпендикулярну до осі у; з центру овалу проводять допоміжні кола d = 0/2D і відмічають точки перетину О₇, О₈, О₉, О₁₀; з точок О₉, О₁₀ проводять дуги mm і m₁m₁ радіусу R = О₁₀ m₁, а з точок О₈, О₇ – дуги радіуса r = О₇ m.

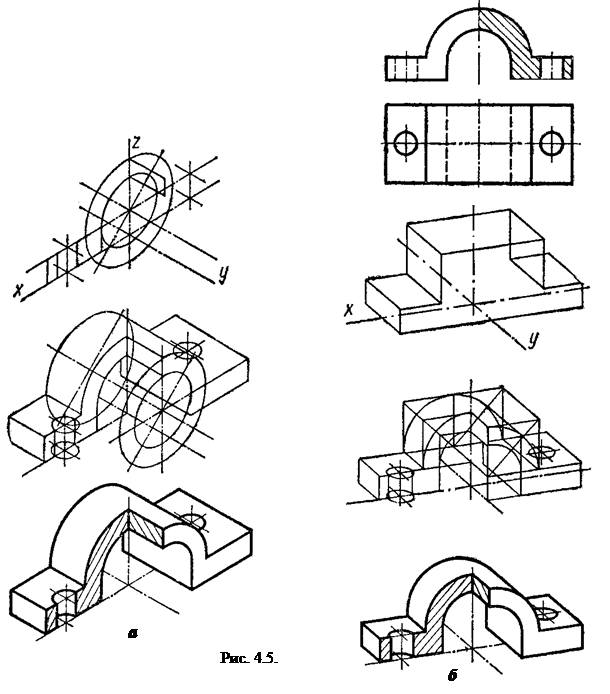На рисунку показана послідовність побудови координатним методом аксонометричних проекцій корпусної деталі з вирізом ¼ (рис. 4.5а – прямокутна ізометрія, рис. 4.5б – прямокутна диметрія.

	Рис. 82

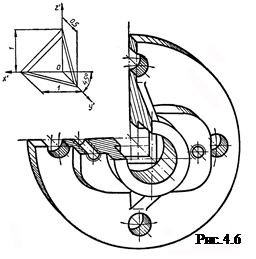Косокутна диметрія. При виконанні фронтальної косокутної диметрії, елементи деталі, що лежать в площинах паралельних до фронтальної площини проекцій, проекціюються на аксонометричну площину без спотворення (рис. 4.6). Кола, розміщені в горизонтальній і профільній площинах проекціюються у вигляді еліпсів, і замінюються овалами, як і в прямокутній симетрії.

Дата добавления: 2014-01-11