Определение подпоследовательности

Пусть 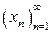– произвольная числовая последовательность.

Пусть 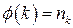функция такая, что

1) 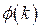определена для ;

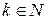2) ;

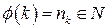3) 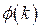возрастающая (строго) функция, т.е.

.

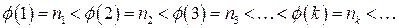Тогда множество 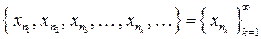элементов исходной последовательности, выделенных с помощью закономерности номеров 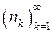, образует подпоследовательность 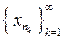исходной последовательности.

Всякая последовательность имеет бесконечное множество
подпоследовательностей, например, 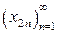,, 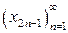и т.д.

Если последовательность сходится, то и любая ее подпоследовательность сходится к тому же пределу.

Если последовательность бесконечно большая, то и любая ее подпоследовательность также бесконечно большая.

Обратные утверждения тоже верны, но не эффективны для изучения поведения последовательности. Поэтому используются обычно теоремы, в которых информация о поведении конечного множества подпоследовательностей позволяет устанавливать свойства исходной последовательности.

Утверждение (достаточное условие сходимости).

Если для произвольной последовательности 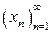ее подпоследователь-ност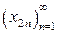и и 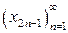сходятся, и их пределы совпадают, то
исходная последовательность 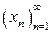сходится к общему значению пределов указанных подпоследовательностей, т.е. ;

.

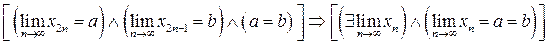Доказательство:

,

.

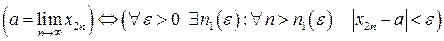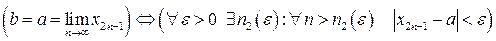Отсюда для всех 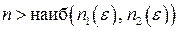имеем ,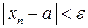
поскольку целое число либо четное, либо нечетное.

Утверждение(достаточное условие "расходимости" последовательности)

Если для произвольной последовательности либо какая-либо ее подпоследовательность не сходится (расходится), либо существуют две ее подпоследовательности, сходящиеся к различным пределам, то сама последовательность расходится.

Типовое задание – показать по определению –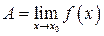
в конкретном случае удобно решать по схеме:

1) рассматриваем произвольное ;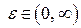

2) ищем 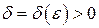так, чтобы ;

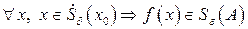3) для этого вычисляем, при каких значениях 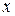выполняется соотношение 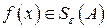, и строим функцию 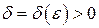с нужными свойствами;

4) записываем вывод.

Пример 1. Показать по определению .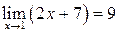

Решение: 1) рассматриваем произвольное;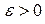

2) ищем 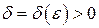так, чтобы ,
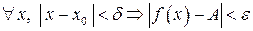т.е. ;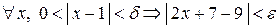

3) вычисляем, при каких значениях 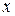верно требуемое неравенство

,

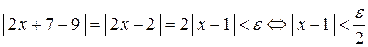т.е. при 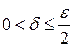из неравенства 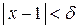следует справедливость неравенства .

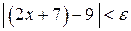Итак,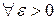

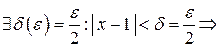
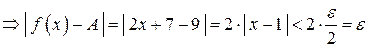, по определению .

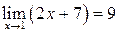Не всегда выбор 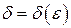с нужными свойствами столь очевиден. Иногда удобнее применить соответствующие (проверенные!) предварительно оценки функций, входящих в решаемые неравенства.

Пример 2. Показать по определению .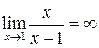

Решение: 1) берем ;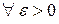

2) ищем 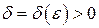так, чтобы ;

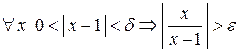3) вычисляем, предварительно оценивая

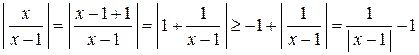
по свойствам абсолютной величины

,

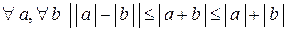причем значение 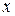считаем близким к 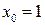так, что ().

Потребуем теперь 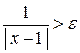и решим это неравенство относительно 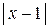, получим .

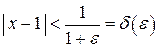Итак, пр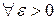и нашли 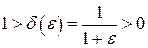так, что

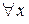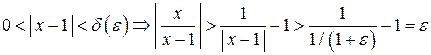, , т.е.

действительно – бесконечно большая при .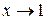

Дата добавления: 2014-01-13