
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Лемма о нуле непрерывной функции
|
|
|
|
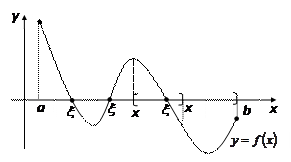
Лемма о нуле непрерывной функции.
Если 1) 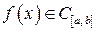 ; 2)
; 2) 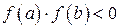 , то
, то 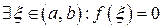 .
.
Для определенности пусть 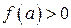 и
и 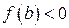 .
.
1. Рассмотрим точку 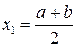 . Если
. Если
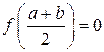 , то
, то 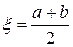 и доказательство закончено, так как
и доказательство закончено, так как 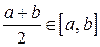 . Если
. Если 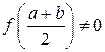 , то число
, то число 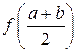 имеет определенный знак, пусть
имеет определенный знак, пусть 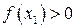 . Выберем тот "половинный" сегмент, на концах которого функция имеет значения противоположного знака. В нашем случае (см. рисунок) это сегмент
. Выберем тот "половинный" сегмент, на концах которого функция имеет значения противоположного знака. В нашем случае (см. рисунок) это сегмент 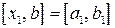 , для него имеем
, для него имеем 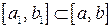 ,
, 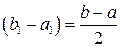 .
.
2. Рассмотрим 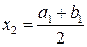 . Если
. Если 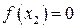 , то
, то 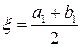 .
.
Если 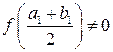 , то выберем сегмент
, то выберем сегмент 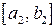 так, чтобы
так, чтобы
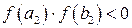 ,
, 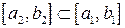 и длина
и длина 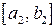 была равна половине длины предыдущего сегмента, т.е.
была равна половине длины предыдущего сегмента, т.е. 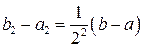 .
.
Процесс продолжим либо до тех пор, пока 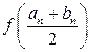 не обратится в ноль, либо при
не обратится в ноль, либо при 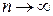 .
.
Получим последовательность сегментов 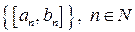 , вложенных и стягивающихся по длине к нулю, для которых (у нас)
, вложенных и стягивающихся по длине к нулю, для которых (у нас) 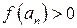 и
и 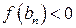 . По принципу Кантора,
. По принципу Кантора, 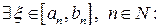
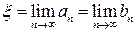 . Воспользуемся теоремой о переходе к пределу
. Воспользуемся теоремой о переходе к пределу
в неравенстве и непрерывностью  на
на 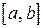 , т.е., в частности,
, т.е., в частности,
в точке 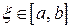 . Получим
. Получим 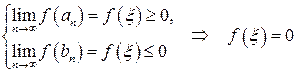 .
.
Замечание. Лемма определяет достаточное условие существования корня уравнения 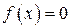 . Если установлено заранее, что на
. Если установлено заранее, что на 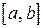 корень единственный, то изложенная в доказательстве процедура построения последовательности сегментов
корень единственный, то изложенная в доказательстве процедура построения последовательности сегментов 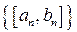 , содержащих корень
, содержащих корень 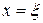 , составляет суть приближенного метода "половинного деления" решения нелинейного уравнения.
, составляет суть приближенного метода "половинного деления" решения нелинейного уравнения.
Обратное утверждение неверно.
Контрпример и примеры на существенность условий леммы
рекомендуем привести самостоятельно.
Теорема Коши (о промежуточном значении)
Если
1) 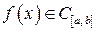 ;
;
2) 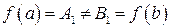 , то для любого числа
, то для любого числа 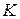 , расположенного между числами
, расположенного между числами 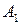 и
и 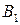 , найдется значение
, найдется значение
аргумента 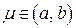 , такое, что
, такое, что 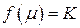 .
.
Доказательство. Функция 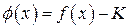 удовлетворяет условиям леммы о нуле непрерывной функции, и поэтому существует
удовлетворяет условиям леммы о нуле непрерывной функции, и поэтому существует 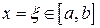 , такое, что
, такое, что 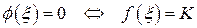 , итак,
, итак, 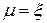 .
.
Теорема доказана.
Замечание. Для функции  , непрерывной на
, непрерывной на 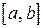 , существует
, существует 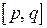 (или
(или 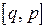 )
) 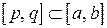 , на концах которого функция достигает своих наименьшего и наибольшего значений
, на концах которого функция достигает своих наименьшего и наибольшего значений 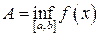 и
и 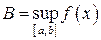 . По теореме Коши всякое промежуточное между
. По теореме Коши всякое промежуточное между 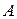 и
и 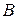 число является значением
число является значением  в некоторой точке сегмента
в некоторой точке сегмента 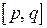 , а значит, и
, а значит, и 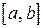 , т.е. непрерывная функция
, т.е. непрерывная функция  отображает сегмент
отображает сегмент 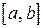 в сегмент
в сегмент 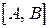 .
.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 561; Нарушение авторских прав?; Мы поможем в написании вашей работы!