Часть II нашего издания полностью посвящена потреблению и потребительскому спросу. 14 страница

Однако все эти характеристики по-прежнему не позволяют ответить на вопрос о том, во сколько раз доходы одних групп населения превышают доходы других. В этом отношении анализ доходов целесообразно дополнить характеристиками, измеряющими разрыв между высокодоходными и низкодоходными группами населения. Такими характеристиками могут являться децильные, квартальные, квантильные и другие коэффициенты, которые подразумевают разбиение исходной совокупности на равные части и измеряют соотношение между доходами двух крайних групп. Если все население разбить на четыре группы и найти отношение среднего дохода последней группы (т. е. той четверти населения, которая имеет наиболее высокие доходы) к среднему доходу первой группы (т. е. группы, включающей низкодоходные слои населения), то мы получим квартальный коэффициент дифференциации доходов. Аналогично, разбив исходную совокупность на пять частей и найдя отношение среднего дохода последней группы к первой, получим квантильный коэффициент дифференциации. При нахождении же децильных коэффициентов совокупность разбивается на 10 равных групп (частей).

Еще один интересный прием анализа доходов населения с точки зрения их дифференциации состоит в расчете так называемых накопленных, или кумулятивных, частот (долей) и построении кумулятивных кривых, или кривых Лоренца (по имени американского статистика М. Лоренца). Рассмотрим на простом примере, как строится кривая Лоренца.

Четыре индивида (назовем их А, В, С и D) получают суммарный доход в 10000 руб. в месяц, который распределяется между ними в соответствии с данными табл. 2. Ясно, что такое распределение дохода не является равномерным. Подсчитав удельный вес дохода каждого индивида в общем доходе, мы можем сказать следующее: наименьшую долю дохода (10 %) получает А; А и В получают 10 + 15 = 25 % дохода, или, иными словами, одна половина людей получает четвертую часть, а другая — три четверти общего дохода.

А, B и С получают 10 + 15 + 30 = 55 % дохода, т. е. на долю D приходится 45 % общего дохода. Полученные последовательным суммированием долей новые удельные веса и называются накопленными, или кумулятивными, частотами. Графически изобразить и измерить неравенство доходов можно с помощью кривой Лоренца. Для ее построения отложим по оси абсцисс последовательно просуммированные удельные веса индивидов в их общем числе, учитывая, что удельный вес каждого из них составляет одну четверть, или 25 %, а по оси ординат — кумулятивные доли доходов этих людей. Соединив все точки, получим кривую Лоренца (рис. 3).

Рис. 3. Кривая распределения доходов четырех индивидов

Таблица 2. Распределение дохода между четырьмя индивидами

	Получаемый доход, руб.	Удельный вес дохода индивида в общем доходе, %	Кумулятивный ряд доходов (накопленные частоты), %	Удельный вес каждого индивида в их общем числе, %	Кумулятивный ряд численности, %
A B C D	1 000 1 500 3 000 4 500	10 15 30 45	10 25 55 100	25 25 25 25	25 50 75 100
Всего	10 000		—		—

Чтобы понять, каким образом эта кривая отражает неравенство доходов, попытаемся ответить на вопрос: какой бы вид имела кривая Лоренца в случае полного равенства доходов? Очевидно, что в такой ситуации каждый получал бы 2500 руб. дохода, т. е. ордината точки А переместилась бы в точку Е, точки B — в точку F и т. д., следовательно, мы получили бы прямую OD, составляющую с осями координат угол в 45о. Таким образом, неравенство доходов характеризуется степенью отклонения кривой Лоренца от биссектрисы 1-го координатного угла. Это отклонение можно измерить через отношение площади заштрихованной фигуры между кривой Лоренца и прямой OD к площади всего треугольника ODK. В результате получим показатель, который в литературе называется коэффициентом концентрации (или коэффициентом Джини (по имени итальянского статистика и экономиста К. Джини)):

G = площадь ODBCA/площадь ODK.

Попробуем рассчитать значение данного коэффициента для нашего примера. Площадь фигуры ODCBA можно с определенной степенью точности найти вычитанием из площади треугольника ODK суммы площадей треугольника OAL и трапеций ABML, BCNM и CDKN, основания которых численно равны накопленным частотам доходов, а высоты — соответствующим удельным весам индивидов. Таким образом, имеем:

ODK = 100.100 = 5000,  

OAL = 25.10= 125,  

ABML = 25 = 437.5,  

BCNM = 25 = 1000,  

CDKN = 25 = 1937.5.

Просуммировав соответствующие площади, получим, что площадь фигуры ODCBA составит 5000 – 3500 = = 1500, поэтому значение коэффициента концентрации для нашего примера будет равно:

G = 1500/5000 = 0.3.

Очевидно, что чем ближе значение этого коэффициента к единице, тем выше дифференциация доходов, и, наоборот, чем ближе его значение к нулю, тем более равномерным является распределение доходов.

Обратимся к данным табл. 3, характеризующим распределение населения СССР по среднедушевому совокупному доходу в 1990 г. и попробуем на основе этих данных построить кривую Лоренца и вычислить значение коэффициента Джини. Однако здесь мы сталкиваемся с некоторыми трудностями. Как видно из предыдущего примера, для построения кривой Лоренца и расчета коэффициента Джини необходимы данные о доле дохода каждой группы населения в совокупном доходе. Эти данные в табл. 3 отсутствуют (в нашей стране они до сих пор не публикуются). Поэтому, чтобы получить некоторое приближение к такому распределению, воспользуемся простым приемом [8]: (см. табл. 3): умножим средние для каждого интервала доходы (определим их как середину интервала) на соответствующие удельные веса (доли) населения, получив тем самым так называемые процентные числа групповых доходов (табл. 3). Затем, рассчитав удельные веса групп в общем доходе и просуммировав их, получим кумулятивный ряд по доходам, выраженный в процентах.

Таблица 3. Распределение населения СССР по среднедушевому совокупному доходу в 1990 г. и расчет накопленных частот

Доход, руб.	Середина интервала, руб.	Удельный вес населения, %	Кумулятивный ряд численности, %	Групповые доходы (процентные числа) (2<+3)	Удельный вес групп в общем доходе, %	Кумулятивный ряд доходов (накопленные частоты), %
До 50 50-75 75-100 100-125 125-150 150-175 175-200 200-250 250 и более	37,5 62,5 87,5 112,5 137,5 162,5 187,5 225,0 275,0	108 5,9 10,6 13,7 14,3 13,2 10,8 14,9 14,8	1,8 7,7 18,3 32,0 46,3 59,5 70,3 85,2 100,0	67,5 368,75 927,50 1 541,25 1 966,25 2 145,00 2 025,00 3 352,50 4 070,00	0,4 2,2 5,6 9,4 11,9 13,0 12,3 20,4 24,8	0,4 2,6 8,2 17,6 29,5 42,5 54,8 75,2 100,00
Всего	—	100,0	—	16 463,75	100,0	—

Источник: СССР в цифрах в 1990 году: Краткий статистический сборник. М., 1991. С. 129.

Нанесем на график точки, абсциссы которых соответствуют кумулятивному ряду численности населения, рассчитанному путем суммирования соответствующих удельных весов населения, а ординаты — кумулятивному ряду доходов (рис. 4). В результате получим кривую Лоренца, отражающую распределение доходов различных групп населения.

Рис. 4. Кривая распределения доходов населения в СССР в 1990 г.

Теперь мы можем рассчитать значение коэффициента концентрации для данной кривой. Просуммировав соответствующие площади, получим, что площадь заштрихованной фигуры составит 5000 – 3846 = 1154, поэтому значение коэффициента концентрации в данном случае будет:

G = 1154/5000 = 0.231.

С помощью кривых Лоренца можно также наглядно продемонстрировать процесс выравнивания доходов через проведение мер налоговой и социальной политики. Так, например, с более высоких доходов при прогрессивном налогообложении взимается более высокий налог, а такие правительственные программы, как социальное страхование, выплата различных пособий, продовольственная помощь, увеличивают доходы относительно бедных слоев населения. При наличии соответствующих данных можно построить кривые Лоренца, отражающие уровни доходов до выплаты налогов, доходов за вычетом налогов и доходов после получения различных выплат и пособий в соответствии с социальными программами (рис. 5), и, сравнив соответствующие коэффициенты концентрации, сделать выводы о влиянии проводимой налоговой и социальной политики на процесс выравнивания доходов населения.

Рис. 5. Распределение населения по доходам с учетом налоговой и социальной политики. а — уровень доходов до уплаты налогов; b — уровень доходов после уплаты налогов; с — уровень доходов после осуществления мер социальной политики.

^[8] Необходимо учитывать, что расчеты данным способом связаны с определенными погрешностями и неточностями, которые следует принимать во внимание при экономической интерпретации результатов.

РАЗДЕЛ 3. Неопределенность равновесия

Теперь, когда мы знаем, как измеряется степень дифференциации денежных доходов, мы можем сравнить их дифференциацию в разных странах.

В табл. 4 приведены данные о распределении денежных доходов по квантилям и коэффициенты концентрации (или коэффициенты Джини) по 11 странам четырех континентов. Внимательно рассмотрите эту таблицу, проверьте расчеты коэффициентов Джини — метод расчета вы знаете — и подумайте, чем объясняются различия в дифференциации доходов в разных странах. Вы обратили внимание на то, что разница в значениях коэффициента Джини в самых богатых и самых бедных странах с рыночной экономикой достигает по абсолютной величине 0.3? А в СССР, как вы помните из раздела 2, в те же годы этот коэффициент составлял лишь 0.241, а к 1990 г. он снизился до 0.231, т. е. был ниже, чем в любой из приведенных в табл. 4 стран. И это при весьма невысоком уровне народного благосостояния.

Таблица 4. Распределение денежных доходов в некоторых странах в начале 80-х гг. (в % к итогу по стране)

Страна	Распределение доходов по 20%-ным группам/div>	Коэффициент Джини
I	II	III	IV	V
Нидерланды Япония Швеция ФРГ США Италия Франция Непал Кения Перу Бразилия	8,0 8,7 7,2 7,9 5,3 6,2 5,3 4,6 2,6 1,9 2,0	14,0 13,2 12,8 12,5 11,9 11,3 11,1 8,0 6,3 5,1 5,0	18,0 17,5 17,4 17,0 17,9 15,9 11,7 11,5 11,0 9,4	23,0 23,1 25,4 23,1 25,0 22,7 21,7 16,5 19,2 21,0 17,0	36,0 36,8 39,5 39,9 43,9 45,8 59,2 60,4 66,6	0,268 0,270 0,291 0,295 0,329 0,347 0,367 0,471 0,525 0,536 0,565

Источник: World Development Report: World Bank, 1984. P. 272-273.

Примечание. Сумма по двум первым строкам отличается от 100.0 из-за ошибок округления.

Как и когда наша страна выбилась из общего строя и “пошла не в ногу” и как пытается теперь “сменить шаг” и найти свое место в этом строю — это мы обсудим немного дальше (см. раздел 5). А сейчас посмотрим, не сказалось ли столь резкое отличие в степени дифференциации доходов на нашем потребительском рынке и если сказалось, то как.

Вы, конечно, уже обратили внимание на то, что кривая спроса обычно имеет отрицательный наклон на всем своем протяжении (слева вниз направо). Эта традиционно принятая полого опускающаяся, вогнутая вверх ее форма является лишь графическим отображением так называемого закона постепенного убывания спроса, который и обеспечивает, как правило, успешное функционирование рыночного механизма.

“Этот закон, — поясняет П. Самуэльсон, — находится в полном соответствии со здравым смыслом и известен в общих чертах по меньшей мере с начала официальной истории человечества. Причины его нетрудно определить. Когда цена пшеницы поднимается до небес, покупать ее в состоянии лишь богатце люди, а бедняки вынуждены обходиться ржаным хлебом.

Если цена пшеницы все еще высока, но уже не в такой степени, как прежде, то ее в небольших количествах могут покупать и лица с умеренными средствами, тоже являющиеся большими любителями белого хлеба” (Самуэльсон П. Экономика. М., 1964. С. 77). Ну а что произойдет в том случае, если общество состоит целиком или по преимуществу из “лиц с умеренными средствами”, если в нем нет богачей и бедняков? И если к тому же все являются “большими любителями белого хлеба”?

Чтобы ответить на этот вопрос, посмотрим, от чего вообще зависит конфигурация кривых спроса. При этом мы будем следовать логике двух известных экономистов — нашего соотечественника Н. Н. Шапошникова и леди из Кэмбриджа Джоан Робинсон (Шапошников Н. Н. Теория ценности и распределения. М., 1912. С. 17—19; Робинсон Дж. Экономическая теория несовершенной конкуренции. М., 1986. С. 61—62.). Мы будем, вслед за этими авторам, называть функцию спроса Q = f(P) вогнутой, если f``(P) > 0, и выпуклой, если f``(P) < 0. Если кривая спроса вогнута, то снижение цены сопровождается нарастающим увеличением объема спроса. Если же кривая спроса выпукла, снижение цены сопровождается падающим ростом объема спроса (рис. 6).

Рис. 6. Вогнутая (а) и выпуклая (б) кривые спроса

Мы можем считать, что кривая индивидуального спроса на обычные товары выпукла, поскольку спрос на них имеет предел насыщения, и в правой части такая кривая имеет вертикальный замыкающий участок. (Если достигнут предел насыщения, снижение цены не дает прироста объема спроса). Значит, если “все покупатели на рынке одинаковы, по уровню достатка и степени предпочтений в отношении данного товара” (Робинсон Дж. Указ. соч. С. 62), то и рыночная кривая спроса, определяемая как горизонтальная сумма индивидуальных кривых (лекция 5), также будет выпуклой. Кривая рыночного спроса будет выпуклой “также в той части, где соответствующая цена настолько низка, что по ней даже самые обездоленные и незаинтересованные покупатели могли бы приобрести какое-то количество данного товара” (там же. С. 62).

И наоборот, рыночная кривая спроса будет, скорее всего, вогнутой, если “спрос предъявляется индивидами с разным уровнем достатка — ведь падение цены не только побуждает тех, кто приобретал этот товар и по более высокой цене, покупать больше, но и создает условия для выхода на рынок новых покупателей. То же самое наблюдалось бы и в том случае, когда степень предпочтения данного товара покупателями была бы неодинаковой (там же. С. 61–62). Если с каждым последующим снижением цены число покупателей со все более низким уровнем дохода или низкой полезностью товара прогрессирующе возрастает, то степень вогнутости рыночной кривой спроса по мере движения вдоль нее вниз и вправо увеличивается.

Таким образом, мы можем заключить, что наличие определенной степени дифференциации доходов (и вкусов) является непременным условием вогнутости рыночных кривых спроса. Формирование традиционной кривой рыночного спроса показано на рис. 7. Вас может удивить ступенчатая, прерывистая конфигурация четырех индивидуальных кривых спроса на этом рисунке (d₁,d₁, d₂,d₂, d₃,d₃, d₄,d₄). Такая их форма обусловлена двумя обстоятельствами.

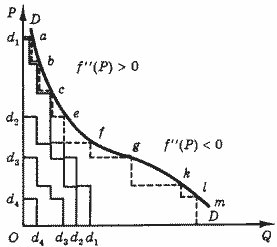
Рис. 7. Формирование рыночной кривой спроса

Недостаточной делимостью благ, во-первых. Это относится не только к таким “крупным” благам, как холодильник, автомашина, телевизор, но и к совершенно делимым благам, которые продаются в определенной расфасовке — банка пива, пломбир, килограммовый пакет муки. Наличием определенного порога покупательской чувствительности, во-вторых. Никакая цена не заставит вас обратиться к продавцу с просьбой взвесить вам ровно 437 г масла, скорее всего вы пожелаете купить или 400, или 500 г, так что объем вашего спроса при изменении цен будет меняться не непрерывно, а дискретно.

Эти соображения дали основание известному русскому экономисту-математику В. К. Дмитриеву сделать важный вывод, который мы разделяем: “Для большинства благ эта функция (индивидуальная функция спроса — В. Г.) является прерывистой (как в силу недостаточной делимости благ, так и в силу недостаточной эластичности потребностей), соответственно этому и кривые частного спроса также будут прерывистые.

Но в силу индивидуальности каждой частной кривой спроса (благодаря чему разрывы в одной не будут соответствовать разрывам в другой) общая кривая спроса, являющаяся результатом суммирования частных кривых, при числе потребителей достаточно большом будет в силу „закона больших чисел“ все же непрерывною” (Дмитриев В. К. Экономические очерки. М., 1904. С. 138).

На рис. 7 ступенчатая линия abcefgkim представляет рыночную кривую спроса, полученную суммированием по горизонтали четырех частных кривых спроса dd, а огибающая плавная кривая DD — кривую спроса при достаточно большом числе покупателей.

Последняя вогнута вверху и выпукла внизу.

Такую форму имеют обычно кривые рыночного спроса в странах с рыночной экономикой, где дифференциация денежных доходов существенна (вернитесь к таб. 4).

В развитых странах доля 10 % высокодоходных семей в общей сумме доходов составляет от 20 % (Япония) до 30 % (Австралия), что равно доле 40—50 % низкодоходных семей. В развивающихся странах доля 10 % высокодоходных семей в общей сумме доходов колеблется от 30 до 50 %, что равно доле 60—80 % низкодоходных.

Рис. 8. Формирование кривой рыночного спроса для пяти покупателей, трое из которых имеют одинаковую частную кривую спроса d₂d₂

Таких контрастов не могло быть и не было в СССР, где коэффициент Джини был в 2.5—3 раза ниже, чем в странах с рыночной экономикой, и где, как вы помните, по словам В. В. Новожилова, денежная единица составляла у разных людей не одинаковую, но и “не очень разную часть индивидуального дохода”. На рис. 8 показано формирование рыночной кривой спроса для случая пяти покупателей, из которых трое имеют одинаковые индивидуальные кривые спроса d₂d₂. Рыночная кривая имеет в этом случае вид ступенчатой линии abcefgk с “широкой” ступенью e. При достаточно большом числе покупателей эта ступенчатая линия приобретает вид плавной ~-образной кривой DD (рис. 9). Как видим, кривая спроса DD имеет форму, отличную от той, что мы получили на рис. 7; в окрестностях точки перегиба она содержит горизонтальный участок, параллельный оси абсцисс.

Рис. 9. ~-образная кривая рыночного спроса

При этом ясно, что равновесная цена, обеспечивающая сбалансированность рынка (отсутствие избытка спроса и избытка предложения) может существовать лишь при сравнительно небольшом или, наоборот, близком к насыщению объеме предложения. Так, если кривая предложения S₁, рынок может быть сбалансирован при цене Р₁, если кривая предложения S₂, рынок может быть сбалансирован при цене Р₂. Но если кривая предложения займет положение S₃, то рынок уже нельзя сбалансировать посредством “назначения” цены Р₃, так как ординате Р₃ на кривой спроса соответствует множество точек с абсциссами от Q₃ до Q₄.

Действительно, при цене Р₃ спрос будет предъявляться в объеме не Q₃, a Q₄ и разность между ними образует избыток спроса, т. е. дефицит. При этом любая попытка повысить цену выше Р₃ приведет лишь к падению спроса и продаж ниже достигнутого уровня (Q₅ < Q₃), а снижение ее — к еще большему увеличению спроса, но не продаж, выше недостижимого пока объема (Q₆ > Q₄) и еще большему росту дефицита. Таким образом, в интервале от Q₃ до Q₄, в том числе и в точке пересечения кривых спроса и предложения, обеспечить равновесие посредством варьирования цен невозможно. Поэтому в условиях значительного сближения денежных доходов и на этой основе индивидуальных потребительских оценок главный способ достижения сбалансированности состоит уже не в варьировании цен, а в резком повышении объема предложения, максимальном сокращении периода насыщения спроса.

Объективная невозможность (и неспособность системы) решить эту задачу, привести распределение реальных благ в соответствие с искусственной, “придуманной” структурой распределения денежных доходов и привела к краху потребительского рынка в стране. Он был фактически заменен системой льгот и привилегий, закрытых распределителей и выездной торговли, “наборов” и “заказов”, распределением “по очереди” и даже “по случаю”. Таким образом, распределение реальных благ существенно оторвалось от распределения доходов. Сближение денежных доходов в таких условиях лишь скрывало фактическую дифференциацию реального благосостояния.

РАЗДЕЛ 4. Расшифрованная статистика

Ни для кого не секрет, что до недавнего времени исследователи, анализирующие процессы распределения заработной платы и доходов различных групп населения в нашей стране, сталкивались с проблемой отсутствия опубликованных статистических данных.

Эти данные были закрыты. Но и те, кто был допущен к такого рода материалам, не могли воспроизвести их в открытой печати иначе, как в форме, малопонятной для рядовых читателей. Поэтому открытые публикации ограничивались лишь косвенными статистическими характеристиками и графическими изображениями распределений населения по размерам заработной платы и доходов (рис. 10).

Рис. 10. Гистограммы распределения заработной платы за 1956, 1957, 1959 и 1964 гг.

Эти показатели и графики базировались на данных выборочных обследований семейных бюджетов и заработной платы, проводимых ЦСУ СССР. Хотя результаты таких обследований не были опубликованы, однако они были доступны некоторым советским экономистам и статистикам, работающим в центральных статистических и плановых органах и ведущим исследования заработной платы и доходов. Работы этих ученых давали достаточное количество информации, позволяющей осуществить реконструкцию большинства имеющихся распределений заработной платы и доходов различных групп населения с достаточной степенью точности.

Опубликованные материалы носят в основном графический характер — это диаграммы, гистограммы или полигоны, представляющие собой распределение заработной платы и доходов населения за отдельные годы.

Для построения гистограммы на оси абсцисс откладываются отрезки, которые в принятом масштабе соответствуют величине интервалов заработной платы или доходов. На этих отрезках затем строятся прямоугольники, площади которых пропорциональны частотам интервала (т. е. удельному весу населения, получающего заработную плату или доход, попадающий в данный интервал). Гистограмма легко преобразуется в полигон, если середины верхних сторон прямоугольника соединить отрезками прямых. Две крайние точки прямоугольников в этом случае замыкаются по оси абсцисс на середины следующих интервалов, в которых частоты равны нулю. Информации такого рода обычно бывает достаточно, чтобы получить возможность реконструкции исходного распределения, и подобная реконструкция широко использовалась западными учеными, особенно с использованием данных, приводимых в работах Н. М. Римашевской и ее коллег (Рабкина Н. Е., Римашевская Н. М. Основы дифференциации заработной платы и доходов населения. М., 1972; Римашевская Н. М. Экономический анализ доходов рабочих и служащих. М., 1965.). Метод, применяемый при осуществлении этой реконструкции, был впервые использован П. Уайлсом и С. Марковским для получения распределения заработной платы за 1966 г (Wiles Р., Markovski S. Income Distribution under Communism and Capitalism // Sov. Stud. 1971. Vol. 22. N 3, 4. Jan., Apr.). Он основан на определенных предположениях о способе, в соответствии с которым создавались первоначальные графики, и подразумевает тщательное измерение гистограмм и полигонов.

Поскольку, как уже говорилось выше, из полигона распределения легко можно получить гистограмму и наоборот, использование данного метода рассмотрим в предположении, что исходным графиком является гистограмма.

В случае, если известен только полигон распределения, мы можем восстановить по нему гистограмму, тщательно его измерив и определив опорные точки (середины интервалов) этого полигона, и затем применить изложенный метод непосредственно к гистограмме. Относительно способа ее построения примем следующие допущения.

1. При построении гистограмм, при уменьшении их размера при опубликовании работы соблюдается определенный масштаб.

2. Граничные значения интервалов заработной платы и доходов, используемые при построении гистограмм, кратны 5.

Реконструкция любого отдельного распределения включает в себя следующие шаги.

1. Определение числа и вероятной ширины столбцов исходной гистограммы.

2. Измерение длин отрезков от оси абсцисс до опорных точек (середин верхних сторон прямоугольников гистограммы) для определения высоты столбцов гистограммы.

3. Вычисление общей площади гистограммы.

4. Измерение степени точности реконструкции путем сопоставления вычисленных по гистограмме средних значений заработной платы или дохода со средними значениями, опубликованными в официальных советских источниках.

5. Определение меры рассеяния и расположения численных значений интервалов исходя из допущения 2 и на основе имеющихся косвенных статистических характеристик.

Применение этого метода рассмотрим на примере реконструкции данных по заработной плате, осуществленной английским экономистом А. Мак-Оли (McAuley A. The Distribution of Earnings and Incomes in the Soviet Union // Sov. Stud., 1977. Vol. 29, N 2. P. 214—237).

В его распоряжении имелись гистограммы распределения заработной платы за 1956, 1957, 1959 и 1964 гг. (Швырков В. В., Аидина Л. К. Модель распределения населения по доходам // Опыт применения математических методов и ЭВМ в экономико-математическом моделировании потребления. М., 1968) (рис. 10).

В соответствии со второй предпосылкой определим масштаб, принятый по оси абсцисс (табл. 5.).

Произведя соответствующие измерения ширины столбцов, получим следующие значения (в руб.) (5₃ — три интервала по 5 руб., 15₆ — шесть интервалов по 15 руб. и т.д.):

1956 г. — 15, 5₃, 156, 203, 30

1957 г. — 15, 5₃, 157, 203, 15

1959 г. — 15, 5₃, 10, 155, 202, 25, 30

1964 г. — 15, 5₃, 106, 15, 20, 25, 30, 25

Таблица 5. Результат измерения гистограммы распределения заработной платы

Масштаб (= 5 р.), мм Нижняя граница первого интервала, руб. Число столбцов Верхняя граница последнего интервала, руб.	3 10 14 220	3 10 15 220	2 15<BR14 225	2 15 17 230

В соответствии с принятым масштабом, зная ширину всех интервалов в рублях, определим нижнюю границу первого интервала и последовательно рассчитаем граничные значения каждого последующего интервала.

Дата добавления: 2014-01-13