
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обратная функция. Производная обратной функции
|
|
|
|
ЧП-чистая прибыль
К-капитал(в учебнике СК-собственный капитал,а в лекции просто К)
П-пассив
А-актив
ФР- финансовый результат
Факторный анализ прибыльности банка
Основные факторы,определяющие финансовый результат
Одним из основных приемов оценки уровня прибыльности коммерческого банка является анализ системы финансовых коэффициентов.
Структурный анализ финансового результата
Показатели оценки доходности и прибыльности коммерческого банка
В качестве основных приемов оценки уровня прибыли коммерчес-
кого банка можно выделить:
• структурный анализ источников прибыли;
• анализ системы финансовых коэффициентов;
• факторный анализ.
Целью структурного анализа является выявление основного источ-
ника прибыли и оценка его с точки зрения стабильности, сохранения в
будущем и перспектив роста.
Пример:
Отчет о прибыли ОАО ВТБ млрд.руб.
| Чистый процентный доход | 69 877 | 58 954 |
| Доходы за вычетом расходов по операциям с ценными бумагами | 18 524 | 16 481 |
| Переоценка позиций, в т.ч. в иностранной валюте | 8 714 | 41 861 |
| Чистый комиссионный и прочие доходы | 13 024 | 18 698 |
| Расходы, св. с обеспечением деятельности и прочие расходы | -28 087 | -20 187 |
| Резервы на возможные потери | -29 921 | -78 566 |
| Прибыль до налогообложения | 61 329 | 35 713 |
| Прибыль | 43 342 | 23 751 |
В 2010 году был обеспечен рост чистой прибыли относительно 2009 года на 75%:
• Основной источник – чистый процентный доход, рост за год – 19%,
• Следующая позиция – доходы от операций с ценными бумагами (за вычетом расходов), рост за год – 12%,
• Значительный источник расходов – формирование резервов на возможные потери, в 2010 имело место значительное сокращение отчислений в резервы – более, чем в два с половиной раза,
• На 40% в 2010 году выросли расходы по обеспечению деятельности банка и прочие расходы.
Система финансовых коэффициентов прибыльности
| Основные показатели | Формула |
| Рентабельность активов | РОА = Чистая прибыль/Активы |
| Прибыль до налогов (ФР)/Активы | |
| Рентабельность работающих активов | Чистая прибыль/Работающие Активы |
| Рентабельность капитала | РОЕ = Чистая прибыль/Капитал |
| Прибыль до налогов/Капитал |
• Темпы роста доходов и расходов,
• Средняя доходность отдельных активных операций, уровень расходов по пассивным операциям,
• Доля активов, приносящих доход в балансе,
• Структура активов и пассивов банка,
• Уровень риска, принятого банком,
• Развитие комиссионных операций.
- ФР/К = (ФР/А)* (А/К)
- ФР/А = (ВД/А) * (ФР/ВД), где
ВД – валовой доход
3. ЧП/К=(ЧП/А)*(А/К)=(ВД/А) * (ЧП/ВД)* (А/К)
(формула Дюпона)-показывает основные направления роста доходности инвесторов коммерческого банка и обеспечения стабильной рентабельности.
Понятие обратимости функции относится к свойствам
функции на множестве (глобальное свойство).
Будем рассматривать функцию 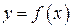 ,
, 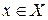 ; здесь
; здесь  – область задания функции:
– область задания функции: 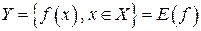 – множество значений функции.
– множество значений функции.
Функция  называется обратимой на
называется обратимой на  , если она принимает каждое своё значение
, если она принимает каждое своё значение 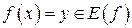 только один раз; символически это определение запишется
только один раз; символически это определение запишется 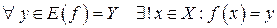
(символ 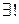 означает "существует единственное значение"),
означает "существует единственное значение"),
т.е. на множестве 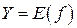 определена функция
определена функция  ,
, 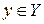 , такая, что выполнены тождества:
, такая, что выполнены тождества:
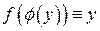 на
на  и
и 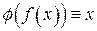 на
на  .
.
При этом функцию 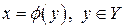 называют обычно обратной функцией для
называют обычно обратной функцией для 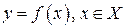 .
.
Заметим, что графики функций 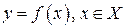 и
и 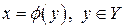 на плоскости OXY совпадают.
на плоскости OXY совпадают.
 Пример. Для функции
Пример. Для функции 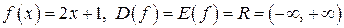 найти обратную функцию; рассмотреть графики прямой и обратной функций.
найти обратную функцию; рассмотреть графики прямой и обратной функций.
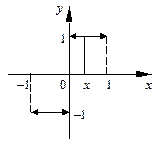
|
Решение. Обозначим 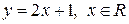 ,
,  ; из этого уравнения находим
; из этого уравнения находим 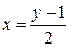 ; видим при этом, что для всякого
; видим при этом, что для всякого 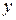 существует единственное значение
существует единственное значение  , т.е.
, т.е. 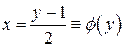 – обратная функция. Графики функций
– обратная функция. Графики функций 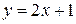 и
и 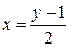 совпадают; это прямая
совпадают; это прямая 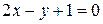 . Заметим, что имеем тождества
. Заметим, что имеем тождества 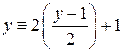 и
и 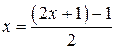 на
на 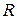 .
.
Для обратной функции  проводим переобозначение
проводим переобозначение
переменных: 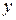 заменяем на
заменяем на  ,
,  заменяем на
заменяем на 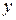 , получаем
, получаем  – функцию, у которой независимая переменная изображается на оси
– функцию, у которой независимая переменная изображается на оси 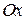 , а значение функции – на оси
, а значение функции – на оси  .
.
В нашем примере переобозначение переменных приводит к функции 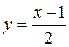 , её график симметричен графику исходной функции относительно прямой
, её график симметричен графику исходной функции относительно прямой 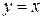 (см. рисунок).
(см. рисунок).
Итак, для нахождения обратной функции для 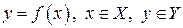 , следует решить (если возможно) уравнение
, следует решить (если возможно) уравнение 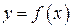 относительно
относительно  ,
, 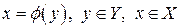 , а затем переобозначить переменные.
, а затем переобозначить переменные.
Функции 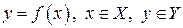 и
и  называются взаимно-обратными, их графики симметричны относительно прямой
называются взаимно-обратными, их графики симметричны относительно прямой 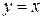 .
.
Достаточное условие существования обратной функции:
Если
1)  – непрерывна на промежутке
– непрерывна на промежутке  ;
;
2)  – строго возрастает (или строго убывает) на промежутке
– строго возрастает (или строго убывает) на промежутке  , то на соответствующем промежутке значений функции
, то на соответствующем промежутке значений функции 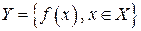 существует однозначная обратная функция
существует однозначная обратная функция  ,
, 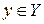 ,
, 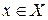 , также непрерывная на
, также непрерывная на  и строго монотонная на
и строго монотонная на  (с сохранением характера монотонности).
(с сохранением характера монотонности).
Доказательство этого утверждения приведено подробно,
например, в [2].
Замечаем, что в условиях утверждения свойства "прямой"
(исходной) функции переносятся на обратную функцию.
Дифференцируемость обратной функции:
если 1) функция 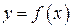 обратима в некоторой окрестности
обратима в некоторой окрестности
точки  ,
, 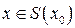 ;
;  ,
, 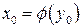 ;
;
2) функция  дифференцируема в точке
дифференцируема в точке  , т.е. существует
, т.е. существует 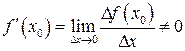 ,
,
то для обратной функции  существует производная
существует производная  и выполняется равенство
и выполняется равенство 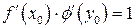 или
или 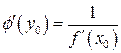 .
.
В самом деле, рассмотрим отношение 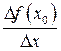 при
при 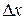 – произ-вольном,
– произ-вольном, 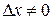 ,
, 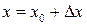 ; получаем
; получаем
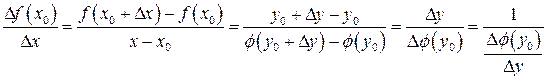 .
.
Поскольку 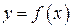 – непрерывна в точке
– непрерывна в точке  (следует из ее дифференцируемости в точке
(следует из ее дифференцируемости в точке  ), то и обратная функция
), то и обратная функция  – непрерывна в соответствующей точке
– непрерывна в соответствующей точке  , т.е.
, т.е. 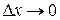 и
и 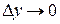 одновременно. И тогда существование предела
одновременно. И тогда существование предела 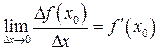 определяет существование предела
определяет существование предела  , причем
, причем 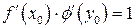 (по теореме о переходе к пределу в равенстве).
(по теореме о переходе к пределу в равенстве).
Формула дифференцирования обратной функции

предполагает выполнимость условий рассмотренной теоремы в
точке  , а также равенства:
, а также равенства: 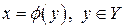 ;
; 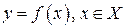 ;
; 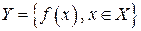 ,
,  на
на  ;
;  на
на  .
.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 794; Нарушение авторских прав?; Мы поможем в написании вашей работы!