
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства операции умножения вектора на число
|
|
|
|
Умножение вектора на число
Определение. Произведением вектора 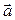 на число
на число 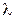 называется вектор
называется вектор  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1. 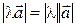 ;
;
2. 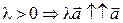 ,
, 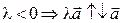 .
.
Следствия. 1. 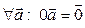 . ►
. ► 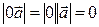
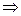
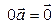 .◄
.◄
2. 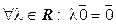 .►
.► 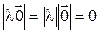
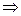
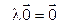 .◄
.◄
3. 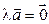
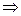
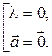 .►
.►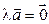
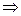
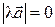
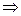
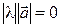
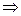
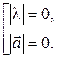
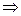
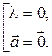 ◄
◄
1. 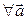 :
: 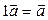 ;
;
2. 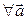 :
: 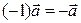 ;
;
3. 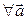
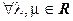 :
: 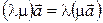 ;
;
4. 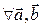
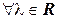 :
: 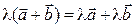 ;
;
5. 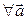
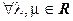 :
: 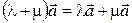 .
.
Первое из приведенных свойств, очевидно, выполняется, докажем остальные.
2. ►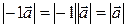 ,
,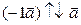 , значит, векторы
, значит, векторы 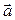 и
и 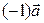 противоположны.◄
противоположны.◄
3. ► Если одно из чисел 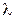 или
или 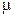 равно нулю, либо вектор
равно нулю, либо вектор 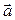 – нулевой, то равенство верно. В любом случае длины векторов в левой и правой частях совпадают, так как
– нулевой, то равенство верно. В любом случае длины векторов в левой и правой частях совпадают, так как 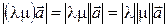 и
и 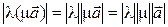 . Остается доказать совпадение их направлений. Если
. Остается доказать совпадение их направлений. Если 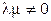 и
и 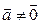 , рассмотрим несколько случаев.
, рассмотрим несколько случаев.
а) 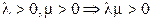 . Тогда
. Тогда 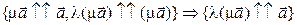 ;
; 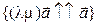 . Таким образом, векторы в левой и правой частях равенства сонаправлены одному и тому же ненулевому вектору, поэтому они также сонаправлены.
. Таким образом, векторы в левой и правой частях равенства сонаправлены одному и тому же ненулевому вектору, поэтому они также сонаправлены.
б) 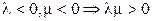 . Тогда
. Тогда  ;
; 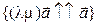 , и опять векторы сонаправлены.
, и опять векторы сонаправлены.
в) 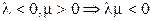 . Тогда
. Тогда 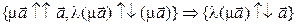 ;
; 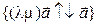 . Векторы в левой и правой частях равенства противонаправлены одному и тому же ненулевому вектору, поэтому они сонаправлены.
. Векторы в левой и правой частях равенства противонаправлены одному и тому же ненулевому вектору, поэтому они сонаправлены.
г) 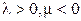 . Случай, аналогичный предыдущему.◄
. Случай, аналогичный предыдущему.◄
 4. ►При
4. ►При 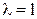 или
или 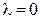 равенство, очевидно, выполняется. Рассмотрим остальные случаи.
равенство, очевидно, выполняется. Рассмотрим остальные случаи.
а) 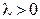 ,
, 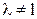 , векторы
, векторы 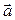 и
и 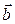 неколлинеарны. От произвольной точки
неколлинеарны. От произвольной точки 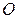 отложим векторы
отложим векторы 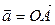 и
и 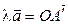 , а от точки
, а от точки 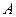 – вектор
– вектор 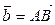 . Проведем прямую через точки
. Проведем прямую через точки 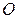 и
и 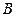 , а через точку
, а через точку 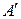 – прямую, параллельную
– прямую, параллельную 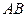 . Точку пересечения построенных прямых обозначим
. Точку пересечения построенных прямых обозначим 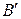 (рис.1.6). Так как
(рис.1.6). Так как 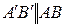 , то треугольники
, то треугольники 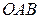 и
и 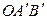 подобны. Из их подобия получаем:
подобны. Из их подобия получаем: 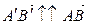 ,
, 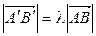 , значит
, значит  ;
; 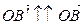 ,
, 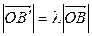 , значит
, значит 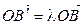 . Тогда
. Тогда 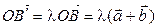 . С другой стороны,
. С другой стороны, 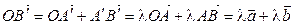 , откуда и вытекает доказываемое равенство.
, откуда и вытекает доказываемое равенство.
 б)
б) 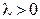 ,
, 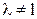 , векторы
, векторы 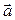 и
и 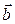 коллинеарны. От произвольной точки
коллинеарны. От произвольной точки 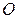 отложим векторы
отложим векторы 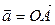 , от точки
, от точки 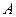 – вектор
– вектор 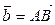 . Выберем произвольную точку
. Выберем произвольную точку 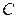 , проведем через нее прямые
, проведем через нее прямые 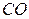 ,
, 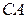 ,
, 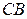 и на прямой
и на прямой 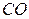 отложим отрезок
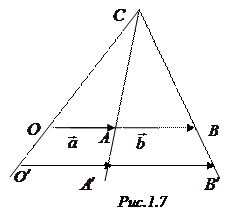
отложим отрезок 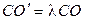 (рис. 1.7). Через точку
(рис. 1.7). Через точку 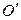 проведем прямую, параллельную
проведем прямую, параллельную  , и обозначим точки ее пересечения с прямыми
, и обозначим точки ее пересечения с прямыми 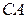 и
и 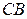 соответственно
соответственно 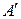 и
и 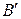 . На рисунке 1.7 треугольники
. На рисунке 1.7 треугольники 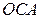 и
и 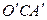 подобны. Из их подобия получаем, что
подобны. Из их подобия получаем, что 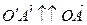 ,
,  , значит,
, значит, 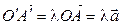 . Аналогично из подобия треугольников
. Аналогично из подобия треугольников 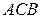 и
и 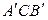 получаем, что
получаем, что 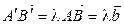 , а из подобия треугольников
, а из подобия треугольников 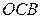 и
и 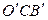 – что
– что 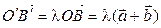 . С другой стороны,
. С другой стороны, 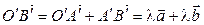 , откуда и вытекает доказываемое равенство.
, откуда и вытекает доказываемое равенство.
в) 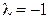 . Вектор
. Вектор 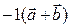 противоположен вектору
противоположен вектору 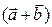 . Но вектор
. Но вектор 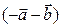 также противоположен
также противоположен 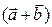 , так как
, так как 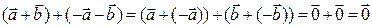 , поэтому
, поэтому 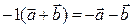 .
.
г) 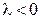 . Тогда
. Тогда
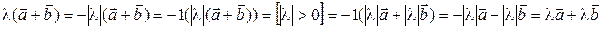 ◄
◄
5. ►а) 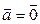 . Равенство, очевидно, выполняется.
. Равенство, очевидно, выполняется.
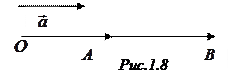 б)
б) 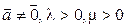 . Тогда
. Тогда 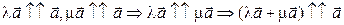 . Но и
. Но и 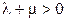 , поэтому
, поэтому 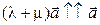 , значит
, значит 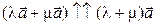 . Остается доказать равенство длин. На рисунке 1.8.
. Остается доказать равенство длин. На рисунке 1.8. 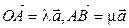 . По рисунку видно, что
. По рисунку видно, что
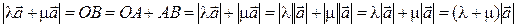 .
.
С другой стороны, 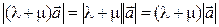 .
.
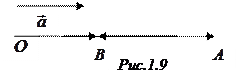 в)
в) 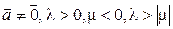 . Тогда
. Тогда 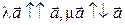 ,
, 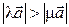 . На рисунке 1.9.
. На рисунке 1.9. 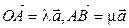 . По рисунку видно, что
. По рисунку видно, что 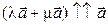 . Кроме того
. Кроме того
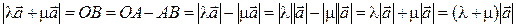 .
.
С другой стороны,  , поэтому
, поэтому 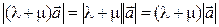 и
и 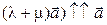 .
.
Аналогично равенство доказывается в случае, когда 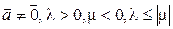 .◄
.◄
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 407; Нарушение авторских прав?; Мы поможем в написании вашей работы!