Решение типовых задач. 5.1. Имеются экспериментальные данные исследования влияния времени вулканизации на сопротивление резины разрыву (табл

5.1. Имеются экспериментальные данные исследования влияния времени вулканизации на сопротивление резины разрыву (табл. 5.5).

Провести на основе приведенных данных исследование взаимосвязи сопротивления резины разрыву и времени ее вулканизации; аналитическое выражение связи проверить на достоверность.

Решение

Результативный признак - сопротивление разрыву (у);

факторный признак — время вулканизации (х).

1. Первичная информация проверяется на однородность по признаку-фактору с помощью коэффициента вариации.

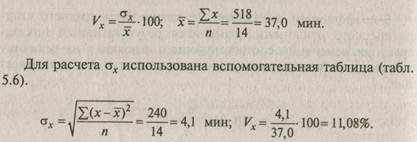
Следовательно, совокупность можно считать однородной, так как V_х менее 33%.

2. Проверка первичной информации на нормальность распределения с помощью правила «трех сигм» (табл. 5.7).

Первичная информация по признаку-фактору не подчиняется закону нормального распределения, однако это не является основанием для отказа использования корреляционно-регрессионного анализа.

Резко выделяющихся единиц в первичной информации нет.

4. Для установления факта наличия связи производится аналитическая группировка по признаку-фактору. Группировка выполняется при равных интервалах и числе групп 4. Величина интервала определяется по формуле

Величина интервала принимается равной 4,0 мин. Ниже построена групповая таблица зависимости сопротивления резины разрыву от времени вулканизации (табл. 5.8).

Для заполнения групповой таблицы была использована вспомогательная таблица (табл. 5.9).

Как видно из данных групповой таблицы (см. табл. 5.8), с увеличением времени вулканизации возрастает величина сопротивления резины разрыву. На рис. 5.1 представлен график связи.

Эмпирическая линия связи приближается к прямой линии. Следовательно, можно считать наличие прямолинейной корреляции.

5. Для измерения степени тесноты связи используется линейный коэффициент корреляции:

Для расчета r использована вспомогательная таблица для расчета линейного коэффициента корреляции и уравнения связи (табл. 5.10).

Значение линейного коэффициента корреляции (r - + 0,925) свидетельствует о наличии прямой и очень тесной связи.

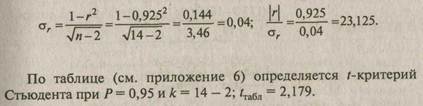
Средняя квадратическая ошибка коэффициента корреляции

Следовательно, можно утверждать существенность коэффициента корреляции.

Для расчета используются данные табл. 5.8.

Следовательно, корреляционное отношение показывает наличие достаточно тесной связи.

Полученное отношение значительно меньше 15%, поэтому уравнение достаточно хорошо отображает взаимосвязь двух признаков и может быть использовано в практической работе.

5.2. По группе предприятий за отчетный квартал имеются следующие данные (табл. 5.11):

На основании приведенных данных требуется:

1) составить уравнение множественной зависимости производительности труда, обосновав систему факторов, включенных в

модель;

2) определить совокупный коэффициент корреляции и частные коэффициенты корреляции;

3) сопоставить роль различных факторов в формировании моделируемого показателя.

Решение

Результативный показатель (производительность труда работника за квартал) — у.

Признаки-факторы:

вооруженность труда основным капиталом — х ₁;

удельный вес оборудования в стоимости основного капитала - х₂;

текучесть кадров — х₃;

интегральный показатель использования рабочего времени — х₄.

Для определения возможности включения факторов в модель строится матрица парных коэффициентов корреляции (с использованием компьютера). Результаты расчета дали следующую матрицу (табл. 5.12).

Цифры первой строки матрицы парных коэффициентов корреляции показывают, что фактор х₃ (текучесть кадров) не следует включать в модель, так как связь результативного показателя с ним слабая (r_х3y = 0,249). С остальными факторами связь тесная, и, если нет мультиколлинеарности, они могут быть включены в модель.

Сначала проверяется возможность включения в модель факторов х₁, и х₂. В качестве критерия принимается соблюдение следующих неравенств:

Решение системы уравнений дает такие значения параметров:

Фактически эти неравенства не соблюдаются, так как

Следовательно, в модель должен быть включен фактор х_1г так как связь результативного показателя с ним более тесная (r_x1y = 0,911).

Далее проверяется возможность включения в модель факторов х₁ и х₄ на основе следующих неравенств:

Фактически эти неравенства соблюдаются, так как

Таким образом, в модель множественной зависимости могу: быть включены два фактора: х ₁ и х ₄. Линейное уравнение имеет

вид:

Система нормальных уравнений для нахождения параметров а. a, b₁ и b₄ следующая:

Модель зависимости производительности труда от факторов имеет вид:

Значения результативного признака, рассчитанные по уравнению связи, представлены в табл. 5.13. По данным этой же таблицы исчисляется средняя квадратическая ошибка уравнения:

Следовательно, уравнение хорошо отображает взаимосвязь производительности труда и двух ее факторов.

Определяется совокупный коэффициент корреляции по формуле

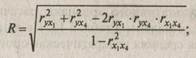
(парные коэффициенты корреляции взяты из матрицы).

Близость совокупного коэффициента корреляции к единице означает: роль не учтенных в модели факторов ничтожна, и есть основания считать, что параметры регрессионной модели отражают степень эффективности включенных в нее факторов. Частные коэффициенты корреляции следующие:

• частный коэффициент корреляции между результативным признаком у и фактором х ₁ при элиминировании фактора х ₄:

• частный коэффициент корреляции между результативным признаком у и фактором х₄ при элиминировании факторах,:

Сопоставление полученных частных коэффициентов корреляции с вычисленными ранее парными коэффициентами корреляции подтверждает наличие тесной связи между результативным и факторными признаками.

Для сравнения роли отдельных факторов в формировании показателя производительности труда определяются коэффициенты эластичности:

Следовательно, при увеличении вооруженности труда основным капиталом на 1% производительность труда возрастает лишь на 0,185%. Увеличение показателя использования рабочего времени на 1% повлечет рост производительности труда на 0,669%.

5.3. По группе однородных предприятий имеются данные об объеме выпущенной продукции и уровне механизации трудоемких и тяжелых работ (табл. 5.14).

Требуется оценить степень тесноты связи между показателями механизации трудоемких и тяжелых работ и объемом продукции при помощи коэффициента Фехнера.

Решение

Для расчета коэффициента Фехнера составляется вспомогательная таблица (табл. 5.15).

Полученное значение коэффициента свидетельствует о наличии связи между уровнем механизации работ и объемом продукции.

5.4. По группе акционерных коммерческих банков региона имеются следующие данные (табл. 5.16).

Исчислить коэффициент корреляции рангов Спирмена для оценки тесноты связи между суммой прибыли банка и размером его активов.

Решение

Для расчета коэффициента корреляции рангов предварительно выполняется ранжирование банков по уровню каждого признака (табл. 5.17).

Дальнейшие расчеты даны в табл. 5.18.

По таблице (приложение 7) определяется при объеме выборки 10 единиц (и - 10) и уровне значимости 5% (а = 0,05) критическая величина для рангового коэффициента корреляции. Она составляет ± 0,6364. Поэтому общий вывод по результату анализа: есть необходимость увеличивать объем выборки.

5.5. В результате обследования работников предприятия получены данные, представленные в табл. 5.19.

Требуется оценить тесноту связи между уровнем образования и удовлетворенностью своей работой с помощью коэффициентов ассоциации и контингенции.

Полученные коэффициенты подтверждают наличие существенной связи между исследуемыми признаками. Однако коэффициент контингенции всегда бывает меньше коэффициента ассоциации и дает более корректную оценку тесноты связи.

5.6. Для изучения влияния условий производства на взаимоотношения в коллективе было проведено выборочное обследование 250 рабочих, ответы которых распределились следующим образом (табл. 5.20).

Требуется охарактеризовать связь между исследуемыми показателями с помощью коэффициента взаимной сопряженности К. Пирсона и А. А. Чупрова.

Сформулировать вывод.

Решение

Коэффициент взаимной сопряженности К. Пирсона определяется по формуле

Коэффициент взаимной сопряженности А. А. Чупрова:

Полученное значение коэффициента взаимной сопряженности К. Пирсона свидетельствует, что связь между условиями производства и взаимоотношениями в коллективе весьма заметна. Коэффициент А. А. Чупрова также не опровергает наличие установленной связи.

Дата добавления: 2014-01-11