Аддитивная мера (мера ХАРТЛИ)

В теории информации важную роль играет комбинаторика чисел и кодов. Введем понятия глубины h и длины числа.

Глубиной h числа называется количество различных элементов, содержащихся в принятом алфавите. Глубине числа соответствует основанию системы считывания и кодирования.

Длиной числа называется количество числовых гнезд,т.е. количество повторений в алфавите, необходимых и достаточных для представления чисел нужной величины. Длина числа сообщает различные системы счислений и кодирования.

Один набор из гнезд-алфавитов составляет одну числовую группу, способную предоставлять и хранить одно полное число длиной . Некоторое количество чисел N представляет числовым полем. При глубине h и длине количество чисел, которые можно представить с помощью числовых групп, выразится формулой:

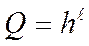
Вследствии показательного закона Q зависит от . Число Q не является удобной мерой для оценки информационной емкости, поэтому Хартли ввел аддитивную двоичную логарифмическую меру, позволяющую вычислять количество информации в двоичных единицах – битах (бит). Для этого берется не само число Q, а его двоичный логарифм:

J = log₂Q = log₂h= log₂h (бит)

Здесь J- количество информации по Хартли.

Если количество разрядов (длина числа) равна единице, имеется в двоичной системе счисления (глубина h=2) и исполняется двоичный логарифм, то потенциальное количество информации равно1 биту.

log₂2=1

Это и есть единица измерения в принятой системе. Она соответствует одному элементарному событию, которая может произойти или не произойти. Аддитивная мера удобна тем, что она обеспечивает возможность считать пропорциональность J относительно числа .

Пример 2

Пусть, например, определятся количество информации, содержащееся в системе, информационная емкость которой характеризуется десятичным числом:

Q = 1000999, h = 10, = 3.

J = log₂Q = log₂10³ = 3 log₂1010

Закодируем это число по двоичной системе h = 2 и найдем :

Q = 2; log₂Q = log ₂2 =

Тогда =log₂1024 = 10 J. Это означает, что в двоичной системе данное число запишется (закодируется) десятью единицами:

Q = 1024 1023 =2⁹+2⁸+2⁷+2⁶+2⁵+2⁴+2³+2²+2¹+2⁰ 1111111111

Другие примеры структурной оценки количества информации.

Дата добавления: 2014-01-13