Статистическая теория

Понятие энтропии

Неопределенность каждой ситуации характеризуется величиной, называемой энтропией. Энтропия в термодинамике означает вероятность теплового состояния вещества, в математике – степень неопределенности задачи, в информатике она характеризует способности источника отдавать информацию. Все эти понятия родственны между собой, а в общем отображают степень богатства и неожиданности состояний.

По ІІ закону термодинамики (закону Больцмана) энтропия замкнутого пространства выражается как

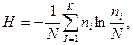
где N – общее количество молекул скорости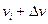

Но есть частота событий и, следовательно, вероятности того, что молекулы имеют скорость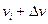

N_i/N=р_i

Тогда . Можно заменить ln на log_2, учитывая, что log₂M

Таким образом, энтропия, полученная разными способами может различаться постоянными коэффициентами перед знаком суммы

.

Энтропия ансамбля

Ансамблем называется полная группа событий или поле несовместимых событий с известным распределением вероятностей, составляющих в сумме единицу.

Энтропия ансамбля есть количественная мера его неопределенности, и следовательно, и информативности.

Энтропия количества выражается, как средняя функция множества вероятностей каждого из возможных исходов опыта, из них n разных, и i-й поход (i=1,2,,n) повторяется n_i раз, и вносит информацию, количество которой оценивается как I. Тогда среднее количество информации, доставляемое одним оптытом равно:

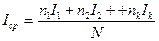
Но количество информации в каждом исходе связанно с его вероятностью p_i и выражается в двоичных единицах (битах) через логарифм:

тогда

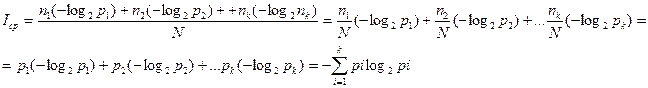где 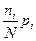-вероятности (частоты) отдельных исходов.

Полученную величину Шеннон назвал энтропией и обозначил буквой Н.

(бит)

Основание логарифма определяет единицу измерения энтропии и количество информации.

-натуральная единица

1 нит =1,44269 бит

lg- десятичная единица

1 дит =3,32193 бит.

Энтропия может быть определена также, как среднее количество информации на одно сообщение или математическое ожидание количества информации I для измеряемой величины х.

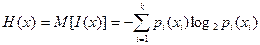
Функция Н(р), где Р=р₁,р₂,..,р_k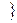-вектор вероятности исходов, была выбрана Шенноном так, чтобы она удовлетворяла следующие требования:

1. Н(р) непрерывна на интервале , т.е. при малых измерениях р величена Н изменяется мало.

2. Н(р) симметрична относительно р, т.е. не изменяется при любой перемене мест аргументов р_i.

3. Н(р₁,р₂,..,р_к-1,q₁,q₂)=H(р₁,р_2,p_k)+p_kH(q₁/p_k,q₂/p_k), т.е. если событие х состоит из двух событий х_i и х_j с вероятностями q₁, q₂, q₁+q₂=p_i, то общая энтропия равна сумме энтропии неразветвленной системы и разветвленной части с весом р_к при условных вероятностях q₁ / p_k и q₂/ p_k

2/1

p₁=2/1

p₂=2/1 q_1/p3=2/3

2/1 1/3

q_2/p3=1/3

1/6

q₁/p₃=2/3 q₂/p₃=1/3

Дата добавления: 2014-01-13