Энтропия объединения

Объединением называется совокупность двух и более взаимозависимых ансамблей дискретных случайных переменных.

Рассмотрим объединение, состоящее из двух ансамблей Х и У, например из двух дискретных измеряемых величин, связанных между собой вероятностными зависимостями.

Схема ансамблей Х:

Х₁ Х₂ Х_i Х_n

p(x₁) p(x₂) … p(x_i) …p(x_n)

Схема ансамблей У:

У₁ У₂ У_j У_m

p(у₁) p(у₂) … p(у_j) …p(у_m)

Схема ансамблей Х и У:

Х₁ Х₂ Х_i Х_n

у₁ p(x₁,у₁) p(x₂, у₁) … p(x_i, у₁) …p(x_n, у₁)

у₂ p(x₁,у₂) p(x₂, у₂) … p(x_i, у₂) …p(x_n, у₂)

:

у_j p(x₁,у_j) p(x₂, у_j) … p(x_i, уj) …p(x_n, у_j)

у_m p(x₁,у_m) p(x₂, у_m) … p(x_i, у_m) …p(x_n, у_m)

Вероятность произведения (совпадения) совместных зависимых событий Х и У равна произведению безусловной вероятности Р(Х) или Р(У) на условные вероятности Р(У/Х) или Р(Х/У). Таким образом, имеем:

Р(Х) Р(У) =Р(Х) Р(У/Х)=Р(У) Р(Х/У)

Отсюда находятся условные вероятности:

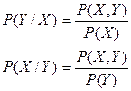
В случае дискретных переменных Х и У частные условные вероятности могут быть записаны для х=х_n как

Р(У₁/Х_К)=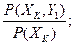Р(У₂/Х_К)= 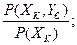Р(У_m/Х_n)=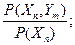

С объединением связаны понятия:

1. Безусловной энтропии

2. Условной энтропии

3. Совместной энтропии

4. Взаимной энтропии

Наименование	Обозначение	Соотношение	Диаграммы
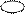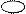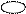Безусловная энтропия	н(х) н(у)	н(х)н(х/у) н(х)=н(х/у)+(х.у) н(у)н(у/х) н(у)=н(у/х)+(у.х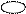)	х у х у
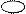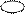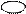Условная энтропия	н(х/у) н(у/х)	н(х/у)=н(х)-н(х.у) н(у/х)=н(у)-н(х.у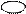)	х у х у
Совместная энтропия	н(х,у)= =н(у,х)	н(х,у)=н(х)+н(у/х)=н(у)+н(х/у)=н(х)+н(у)-н(х.у)	х у х у
Взаимная энтропия	н(х,у) =н(у,х)	н(х.у)=н(х)-н(х/у)=н(у)-н(у/х)=н(х,у)-н(х/у) -н(у/х)	х у х у

Различные виды энтропии в данной таблице имеют следующий смысл:

н(х)-безусловная энтропия источника или среднее количество информации на символ, выдаваемое источником.

н(у)-безусловная энтропия приемника или среднее количество информации на символ, получаемое приемником.

н(х у)-взаимная энтропия системы передачи-приема в целом или средняя информация на пару символов (переданного и принятого).

н(х/у)-условная энтропия х относительно у или мера количества информации от источников, когда известно, что принимается у.

н(у/х)-условная энтропия у относительно х или мера количества информации в приемнике, когда известно, что принимается х.

н(х,у)-совместная энтропия х и у или среднее количество информации выдаваемое источником и принятое приемником.

На основании статистических данных могут быть установлены вероятности событий у₁,у₂,…,у_m при условии, что имеют место события х_i, a именно

р(у₁/х₁), р₁(у₂/х_i),…, р(у_m/х_i)

Тогда частная энтропия равна

н(у/х_i)=-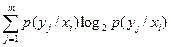

Энтропия для всех переданных сигналов равна:

н(у/х)=-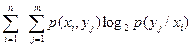

Аналогично получается условная энтропия:

н(х/у) н(х/у)=-

Безусловная энтропия ансамбля х равна:

н(х)=-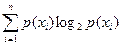

Безусловная энтропия ансамбля у равна

н(у)=-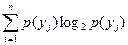

Дата добавления: 2014-01-13