Математическое описание дискретизации

В основе математического описания дискретизации непрерывных функции во времени может так называемая импульсная функция дискретизации , представляя собой периодическую последовательность 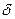-функций, следующих через интервалы времени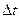

(1)

Используя преобразование Фурье, получим спектр импульсной функции дискретизации:

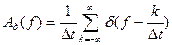(2)

который представляет собой периодическую последовательность 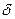- функции, следующих через частотные интервалы .

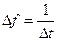В соответствии со свойством 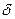- функций

,

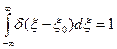площадь каждой составляющей 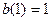a . Эти значения площадей определяют “веса” 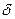-функции.

Дискретизация непрерывных функций времени 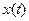с математической точки зрения представляет собой умножение этой функции на функцию

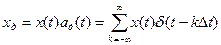(3)

В соответствии с фильтрующим свойством 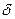- функции

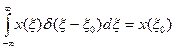(4)

имеем

(5)

(5) означает, что умножение 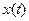на единицу 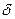- импульса приводит к тому, что значение этого импульса становится равной вместо 1 значения 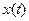в момент .

Эту площадь обычно называют весовым коэффициентом 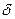- импульса. Иными словами, умножение 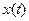на единицу 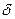- импульса соответствует, получению отчета функции 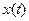в момент .

С учетом (5)(3):

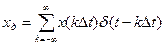
Следовательно, умножение 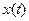на приводит к преобразованию периодической последовательности 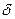- импульсов, веса которых равны мгновенным значениям сообщении в моменты .

На практике реализовать в виде 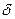- импульсов невозможно. Технически дискретизация непрерывных сообщений реализуется ключевыми устройствами, управляемыми периодической последовательностью коротких импульсов. При этом длительность отчетов конечно, поскольку отчет берется не в одной точке, а в некотором интервале времени равном длительности импульса 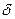. Если выбрать , так, чтобы выполнялось , образуется последовательность коротких импульсов, амплитуды которых пропорциональны мгновенным значениям сообщения.

Практическая реализация дискретизации по времени часто называют импульсным преобразованием непрерывного сообщения (АИМ).

При решении задач дискретизации по времени возникает ряд вопросов:

1. Из каких соображений надо исходить при выборе интервала ;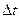

2. Какова точность замены непрерывного сообщения последовательностью его отчетов,

взятых в дискретные моменты, и от чего она зависит;

3. Каков максимально допустимый интервал 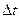, при котором еще принципиально

возможно восстановление непрерывных сообщении.

Решить эти задачи можно только в случае, если проблему дискретизации рассматривать в неразрывной связи с обратной проблемой – восстановлением непрерывных функции времени по мгновенным значениям, известным только в дискретные моменты времени. Сложность этой проблемы заключается в том, что нужно восстановить утраченные при дискретизации сведения о поведении непрерывных функции. В промежутке между отчетами.

Очевидно, чем меньшим количеством отчетов в сообщении заменяется сообщение длительностью Т, тем продолжительнее 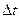, и сложнее выполнить восстановление исходных функции. И наоборот, чем больше отчетов, тем короче 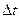и тем проще восстановление.

Т.О, рассматриваемая проблема дискретизации не имеет однозначные решения. Осуществление более экономного импульсного преобразования непрерывного сообщения связана с усложнением задачи восстановления, а неэкономичное импульсное преобразование приводит к упрощению процедуры восстановления.

Дата добавления: 2014-01-13