Робота консервативних сил дорівнює зміні потенціальної енергії, взятій з протилежним знаком

Знайдемо потенціальну енергію в деяких випадках.

1) Потенціальна енергія м.т. в однорідному полі сили тяжіння.

Якщо м.т. впаде з висоти h на нульовий рівень (відносно якого й відлічувалась h), то сили тяжіння виконають роботу A=mgh. Отже на висоті h м.т. має потенціальну енергію U=mgh+C. Стала С дорівнює потенціальній енергії на нульовому рівні; вважаючи, що вона рівна нулю, одержимо:

U=mgh

(7.13)

2) Потенціальна енергія деформованої пружини.

Пружні сили є центральними силами, тому вони консервативні. Ці сили підлягають закону Гука:

,

де – розтяг (чи стиск) пружини (див. рис. 7.9). Точка прикладання сили пружності здійснює переміщення від 0 до x:

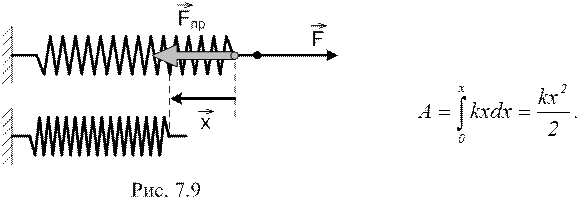
Вважаючи потенціальну енергію пружної деформації в недеформо-ваному стані рівною нулю, одержимо:

(7.14)

3. Потенціальна енергія гравітаційної взаємодії двох матеріальних точок.

Будемо вважати потенціальну енергію взаємодії двох м.т., які знаходяться нескінченно далеко одна від одної, рівною нулю. Робота переміщення м.т. m₂ в нескінченність дорівнює:

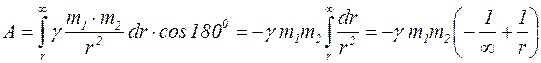
Отже:

(7.15)

Якщо тіла наближаються одне до одного, то їх потенціальна енергія зменшується; при вказаному вище виборі нульового рівня вона буде від’ємною.

4. ЗВ’ЯЗОК МІЖ ПОТЕНЦІАЛЬНОЮ ЕНЕРГІЄЮ ТА СИЛОЮ.
ПОТЕНЦІАЛ ПОЛЯ.

За означенням роботи (див. (7.2)): . З іншого боку в полі консервативних сил: 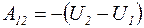(див.(7.12)) Прирівняємо праві частини цих виразів:

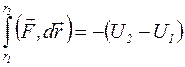. Врахуємо, що :

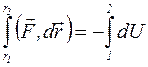
З останнього співвідношення випливає рівність підінтегральних виразів:

.

Розглянувши переміщення вздовж однієї вісі, наприклад OX, одержимо:

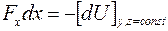, звідки: 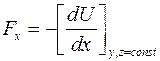. Вираз справа – це частинна похідна:

Аналогічно для осей OY та OZ:

.

Для вектора :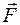

,

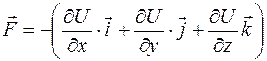(7.16)

де координатні орти.

Вираз в дужках називають градієнтом скалярної функції U:

(7.17)

Таким чином, зв'язок між потенціальною енергією частинки і силою, що на неї діє в полі, дає вираз (7.17): сила 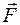дорівнює взятому зі знаком мінус градієнту потенціальної енергії частинки в даній точці поля.

Градієнт позначають також знаком 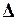(«набла»): де 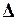означає символічний вектор або оператор:

, який називають оператором Гамільтона.

Поділимо (7.17) на масу точки m: .

Відношення 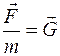– це напруженість гравітаційного поля; відношення називають потенціалом гравітаційного поля в точці, радіус-вектор якої дорівнює . Отже:

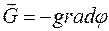
(7.18)

Враховуючи наведене раніше означення потенціальної енергії, можна дати й інше означення потенціалу:

Потенціалом даної точки гравітаційного поля називають відношення роботи переносу точкового тіла масою m з даної точки в нульову до маси цього тіла:

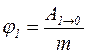
(7.19)

Якщо гравітаційне поле створюється точковою масою, то:

(7.20)

В (7.20) нульовий рівень потенціальної енергії обрано в нескінченності.

Як і у випадку потенціальної енергії однозначно визначена лише різниця потенціалів точок 1 і 2:

(7.21)

звідки:

Якщо гравітаційне поле створене декількома матеріальними точками, то потенціал цього поля дорівнює алгебраїчній сумі потенціалів полів, які створені окремими м.т.:

(7.22)

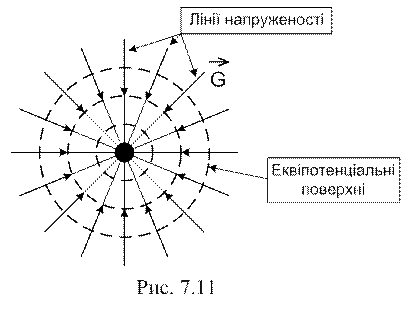
Лінії, дотичні до яких визначають напруженість гравітаційного поля, називають лініями напруженості або силовими лініями гравітаційного поля.

Поверхні, точки яких мають однаковий потенціал, називають еквіпотенціальними поверхнями.

З виразу (7.18)одержуємо: 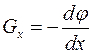; оскільки 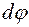вздовж еквіпотенціальної поверхні дорівнює нулю, то вектор перпендикулярний до еквіпотенціальної поверхні (рис. 7.11).

Використовуючи вищенаведене, можна так визначити фізичний смисл :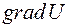

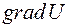– це вектор, направлений по нормалі до еквіпотенціальної поверхні в сторону зростання потенціальної енергії U.

Оскільки 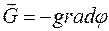, то напруженість гравітаційного поля направлена в сторону зменшення потенціалу.

5. ЗАКОН ЗБЕРЕЖЕННЯ ЕНЕРГІЇ В КОНСЕРВАТИВНІЙ СИСТЕМІ.

Згідно з теоремою про кінетичну енергію сума робіт всіх сил, що діють на матеріальну точку, дорівнює приросту кінетичної енергії цієї м.т.:

(7.10)

З іншого боку робота консервативних сил дорівнює зміні потенціальної енергії, взятій з протилежним знаком:

(7.12)

Для консервативних сил праві частини рівностей (7.10) і (7.12) можна прирівняти:

.

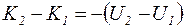Після перетворень одержимо:

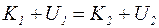
(7.23)

Сума кінетичної та потенціальної енергії системи називається повною механічною енергією Е:

K + U = E

Отже, в ізольованій консервативній системі повна механічна енергія залишається сталою. Можуть відбуватися лише перетворення потенціальної енергії в кінетичну і навпаки, а повний запас енергії системи змінитись не може.

Це положення (і рівняння (7.23)) називають законом збереження механічної енергії.

Оскільки кінетична енергія завжди додатна (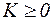), то повна енергія завжди більша потенціальної: . Це співвідношення визначає межі зміни координат системи, в яких вона може перебувати при заданій повній енергії Е. Там, де U > E, система перебувати не може. Наведемо приклад для одномірного руху м.т. вздовж вісі OX. Потенціальна енергія м.т. є функцією від x: 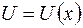. Графік цієї функції називають потенціальною кривою (рис. 7.12). Якщо повна енергія частинки , то вона може рухатись або в зоні між 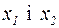(здійснювати коливання), або правіше 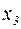. Перейти ж з першої зони в другу частинка не може: цьому заважає потенціальний бар’єр BNC, що розділяє ці зони. Частину потенціальної кривої AMB називають потенціальною ямою для цієї частинки.

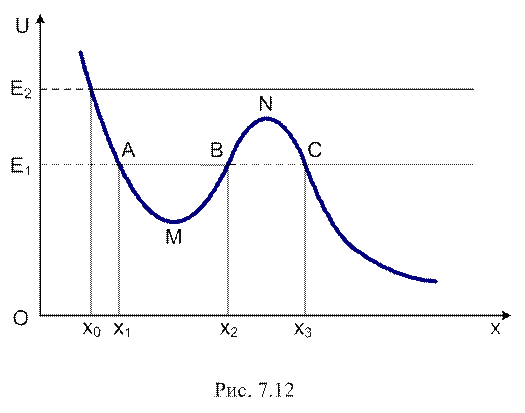
Зону AB називають областю фінітного руху, зону - областю інфінітного руху м. т. з енергією Е₁. Інакше веде себе частинка з енергією Е₂: для неї доступна вся область правіше координати 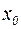. Якщо в початковий момент часу частинка перебувала в точці з координатою 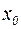, то далі вона буде рухатись вправо; її кінетична енергія буде зростати до т М, потім зменшуватись до т N і далі зростатиме.

6. ВНУТРІШНЯ ЕНЕРГІЯ. ЗАКОН ЗБЕРЕЖЕННЯ ЕНЕРГІЇ
В НЕКОНСЕРВАТИВНІЙ СИСТЕМІ.

Нехай в системі поряд з консервативними і гіроскопічними силами діють також дисипативні сили. За теоремою про кінетичну енергію робота всіх сил 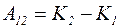. Цю роботу можна представити у вигляді суми роботи консервативних сил і роботи дисипативних сил:

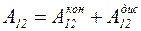
(7.24)

Перший доданок дорівнює . Підставивши вирази для і в (7.24), одержимо:

.

.

.

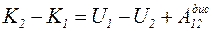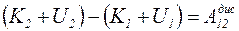(7.25)

Оскільки робота дисипативних сил від’ємна, то < , тобто, механічна енергія неконсервативної системи зменшується. Це можна спостерігати під час удару свинцевих чи пластилінових куль, в системах з тертям, при деформаціях, що перевищують межу пружності. Однак завжди при втраті механічної енергії в системі відбуваються які-небудь внутрішні зміни (наприклад, нагрівання тіл). Враховуючи молекулярну будову речовини, можна сказати, що механічна енергія макроскопічного руху переходить в кінетичнуенергію безладного руху молекул речовини а також в потенціальну енергію їх взаємодії. Ця частина енергії тіла одержала назву внутрішньої. Розширивши поняття енергії, ввівши нові її форми: енергію електромагнітного поля, ядерну енергію та ін., можна сформулювати загальний закон збереження енергії, що є узагальненням дослідних фактів і не знає ніяких винятків: енергія ніколи не створюється і не знищується, вона може лише переходити з однієї форми в другу.

(Застосування законів збереження енергії та імпульсу до аналізу пружного і непружного ударів – розглянути самостійно. Див., наприклад, Александров Н.В., Яшкин А.Я. Курс общей физики: Механика. – М.: Просвещение, 1978. – с. 162-169).

Дата добавления: 2014-01-11