Отсечение многоугольников

Управление двухмерными объектами

Для управления объектом в ИМГ используют следующие методы:

Масштабирование;

Перенос;

Вращение.

Если замкнутый многоугольник отсекается, как набор отрезков, то исходная фигура может превратиться в один или более открытых многоугольников или просто стать совокупностью разрозненных отрезков, как показано на рисунке. Однако если многоугольники рассматриваются как сплошные области, то необходимо, чтобы замкнутость сохранялась и у результата. Для примера на рисунке это означает, что отрезки B’C’, E’F’, F’G’ и H’A’ должны быть к описанию результирующего многоугольника. Добавление отрезков E’F’ и F’G’ представляет особые трудности.

Рис. 1-8

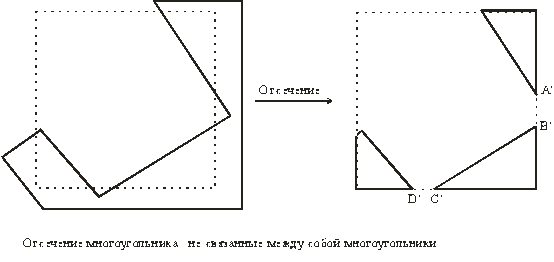
Рис. 1-9

Трудные вопросы возникают и тогда, когда результат отсечения представляет собой несколько несвязанных между собой многоугольников меньших размеров, как это показано на рисунке. Например, иногда отрезки A’B’ и C’D’ включаются в описание результата. Если, например, исходный многоугольник объявлен красным на синем фоне, то отрезки A’B’ и C’D’ тоже будут выглядеть красными на синем фоне. Это противоречит ожидаемому результату.Последовательное отсечение многоугольника: алгоритм Сазерленда-Ходжмена

Основная идея алгоритма Сазерленда-Ходжмена состоит в том, что отсечь многоугольник относительно одной прямой или плоскости очень легко. В этом алгоритме исходный и каждый из промежуточных многоугольников отсекается последовательно относительно одной прямой. Работа алгоритма для прямоугольного окна показана на рисунке. Исходный многоугольник задается списком вершин P1,…, Pn, который порождает список его ребер P1P2, P2P3, …, Pn-1Pn, PnP1. На рисунке показано, что многоугольник сначала отсекается левой стороной окна, в результате чего получается промежуточная фигура. Затем алгоритм вновь отсекает эту фигуру верхней стороной окна. Получается вторая промежуточная фигура.

Рис. 1-10

Далее процесс отсечения продолжается оставшимися сторонами окна. Заметим, что добавление угловой точки Q8 в окончательный результат отсечения теперь стало тривиальным. Этот алгоритм способен отсекать любой многоугольник, выпуклый или невыпуклый, плоский или неплоский, относительно любого окна, являющегося выпуклым многоугольником. Порядок отсечения многоугольника разными сторонами непринципиален.

Результатом работы алгоритма является список вершин многоугольника, у которого все вершины лежат по видимую сторону от очередной отсекающей плоскости. Поскольку каждая сторона многоугольника отсекается независимо от других, то достаточно рассмотреть только возможные ситуации расположения одного отрезка относительно одной отсекающей плоскости. Будем рассматривать каждую точку Р из списка вершин многоугольника, за исключением первой, как конечную точку ребра, начальной точкой S которого является вершина, предшествующая Р в этом списке. Тогда возможны только четыре ситуации взаимного расположения ребра и отсекающей плоскости. Они показаны на рисунке.

Результатом каждого сопоставления ребра многоугольника с отсекающей плоскостью будет занесение в список вершин результирующего усеченного многоугольника нуля, одной или двух вершин.

Если рассматриваемое ребро полностью видимо, то результатом будет вершина Р.

Рис. 1-11

Взаимное расположение ребер и отсекающей плоскости.

Заносить в результат начальную вершину S в этом случае не надо, так как если вершины рассматриваются поочередно, то S уже была конечной точкой предыдущего ребра и поэтому уже попала в результат. Если же ребро полностью невидимо, то результат не изменяется.

Если ребро многоугольника видимо не полностью, то оно может или входить или выходить из области видимости отсекающей плоскости. Если ребро выходит из области видимости то надо определить и занести в результат точку пересечения ребра и отсекающей плоскости. Если же ребро входит в область видимости, то следует поступить точно также. Поскольку в последнем случае конечная вершина Р ребра видима, то она также должна попасть в результат.

Для первой вершины многоугольника необходимо определить только факт ее видимости. Если вершина видима, то она попадает в результат и становиться начальной точкой S. Если же вершина невидима, она тоже становиться начальной точкой, но в результат не попадает.

Последнее ребро-PnP1 – следует рассмотреть особо. Это реализуется путем запоминания первой вершины многоугольника в F. Тогда последним ребром становиться PnF, и его можно обрабатывать точно так же, как и любое другое ребро.

1.4.1. Последовательное отсечение многоугольника:алгоритм Вейлера - Азертона

Рассматривается два многоугольника:

· 1-ый-отсекаемый

· 2-ой-отсекающий

Рис. 1-12

Если ребро входит в отсекающий многоугольник (2) при обходе по часовой стрелке, то продолжается обход исследуемого многоугольника.

Если ребро выходит из отсекаемого многоугольника (1), то проиводится поворот направо с запоминанием точки пересечения.

Точки пересечения добавляются в список вершин.

Рис. 1-13

Как обрабатываемый, так и отсекающий многоугольники описываются в алгоритме циклическими списками их вершин. Внешняя граница каждого из этих многоугольников обходиться по часовой стрелке, внутренние границы или отверстия- против часовой стрелке. Это условие означает, что при обходе вершин многоугольника в порядке их следования в соответствующем списке внутренняя его область будет расположена справа от границы. Границы обрабатываемого и отсекающего многоугольников могут пресекаться или не пересекаться между собой. Если они пересекаются, то точки пересечения образуют пары. Одно пересечение из пары возникает когда ребро обрабатываемого многоугольника входит внутрь отсекающего многоугольника, а другое- когда оно выходит оттуда. Основная идея заключается в том, что алгоритм начинает с точки пересечения входного типа, затем он прослеживает внешнюю границу по часовой стрелке до тех пор, пока не обнаруживается еще одно пересечение с отсекающим многоугольником. В точке последнего пересечения производиться поворот направо и далее прослеживается внешняя граница отсекателя по часовой стрелке до тех пор, пока не обнаруживается ее пересечение с обрабатываемым многоугольником. И вновь в точке последнего пересечения производиться поворот направо и далее прослеживается граница обрабатываемого многоугольника.

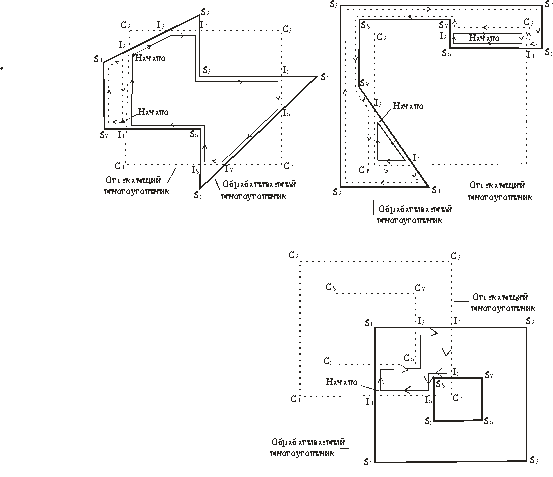
Рис. 1-14

Дата добавления: 2014-01-13