Представление периодических функций времени в частотной области. Ряд Фурье

Описание электромагнитых влияний в частотной и временной областях

В принципе электромагнитные влияния могут рассматриваться как во временной, так и в частотной области. Однако поскольку передаточные свойства путей связи и средств помехоподавления удобнее представлять в частотной области, такое представление чаще всего предпочитают и для помех. Пересчет периодических процессов из временной области в частотную выполняют при помощи ряда Фурье, пересчет однократных импульсных процессов - при помощи интеграла Фурье.

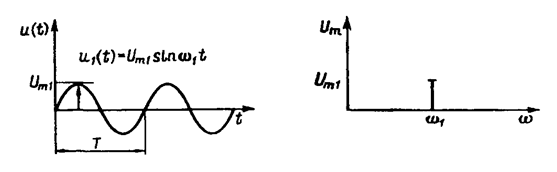
Синусоидальные или косинусоидальные помехи (гармонические процессы) могут быть представлены как во временной, так и в частотной областях непосредственно (рисунок 6.6). В частотной области помеха характеризуется угловой частотой ω и частотой колебаний .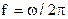

Несинусоидальные периодические функции - например, пилообразной или прямоугольной формы импульсы напряжения или тока выпрямителей которые, в некоторых случаях, возможно описать аналитически, - могут быть представлены в частотной области как бесконечная сумма синусоидальных и косинусоидальных колебаний, т. e. рядом Фурье.

Рисунок 6.6 - Представление синусоидальной помехи вовременной

и частотной областях

Например, можно представить себе несимметричное напряжение прямоугольной формы возникшим как наложение основного колебания и основной частоты 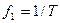и бесконечно многих гармонических колебаний 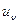с частотами 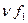Зависимость амплитуды отдельных колебаний от частоты представляет собой дискретный линейчатый спектр (рисунок 6.7.) Наименьшая встречающаяся в линейчатом спектре частота - основная частота.

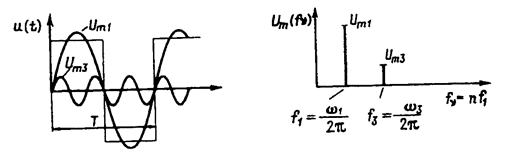Частоты высших гармоник являются значениями, кратными этой основной частоте, например .

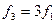Рисунок 6.7 - Периодическая несинусоидальная функция

Аналитически ряд Фурье любой функции времени может быть представлен в различных формах:

Нормальная:

,

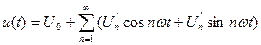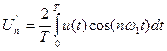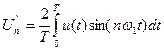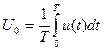, , . (6.1)

Коэффициенты 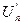и 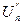- амплитуды отдельных колебаний. Составляющая 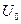соответствует среднему арифметическому значению функции времени (постоянная составляющая).

Амплитудно-фазовая: Так как синусоидальные колебания c соответствующим фазовым сдвигом могут быть представлены и как косинусоидальные, например 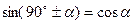, вместо нормальной формы часто применяют амплитудно-фазовую форму:

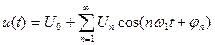, (6.2)

где ;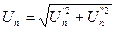

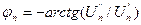
Комплексная.

Если дополнять вышеприведенные уравнения мнимой частью и заменить тригонометрические функции по формуле Эйлера 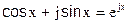экспоненциальными функциями, получаем уравнение в комплексной форме:

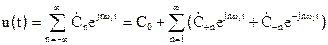, (6.3)

где ,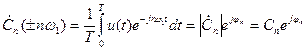

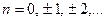
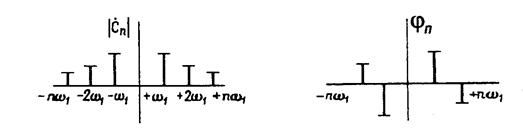
Рисунок 6.8 - Амплитудный и фазовый спектры комплексного ряда Фурье

Так как функция 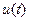будучи представленная комплексным рядом Фурье (6.3.) остается действительной, то в правой части вводятся отрицательные частоты (чтобы мнимые части сократились). Учет отрицательных частот приводит к двустороннему спектру (рис. 6.8.). Идентичные вещественные части обоих слагаемых в (6.3.) за знаком суммы (для положительных и отрицательных частот 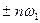) образуют физически измеримую амплитуду 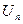, причем

, .

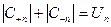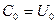При анализе ЭМС вместо двустороннего математического спектра 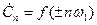чаще всего рассчитывают односторонний «физический» спектр 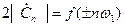только для положительных n, амплитуды которого отличаются на коэффициент 2 от амплитуд двустороннего спектра. Значения амплитуд одностороннего спектра измеримы, они совпадают со значениями коэффициентов косинусоидальной формы, т.е. соответствуют значительным час­тям векторов переменного напряжения той же частоты.

В заключение на рисунке 6.10. показаны импульсы прямоугольной формы двух периодически изменяющихся напряжений одной и той же основной частоты, однако различной скважности, и относящиеся к ним линейчатые спектры. Из вышесказанного можно установить следующее: наименьшая частота 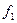является основной частотой. Ее значение связано со значением периода Т: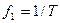

Амплитуды высших гармоник появляются с одинаковым интервалом 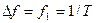их частоты кратны основной частоте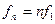

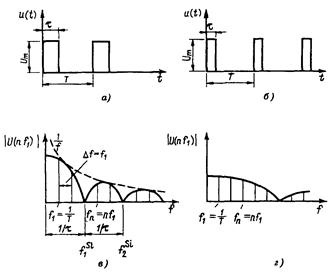
Рисунок 6.10 - Линейчатые спектры двух периодических последовательностей прямоугольных импульсов напряжений с личной скважностью (1:2):

функция 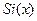- огибающая спектральных амплитуд (сплошная кривая); функция 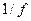- огибающая функции 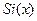(пунктирная кривая)

Ряд Фурье для последовательности прямоугольных импульсов имеет вид:

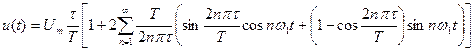
Коэффициенты (спектральные амплитуды) (без постоянной составляющей) определяются формулой:

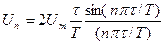
Огибающая спектральных амплитуд следует функции 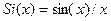.Первое значение нуля этой функции соответствует обратной величине длительности импульса

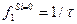
Другие нулевые значения следуют с интервалом . На практике нулевые значения появляются не столь явно выраженными, как на рис. 1.10, так как из-за неизбежных асимметрий (например, экспоненциальных нарастаний и спада прямоугольных импульсов) они сглаживаются.

Постоянный коэффициент при функции 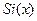равный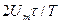при неизменном периоде пропорционален площади импульса 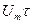. Таким образом, высокие узкие импульсы при низких частотах могут иметь такой же спектр, как низкие широкие. Поэтому в вышеприведенном примере спектральные амплитуды из-за меньшей на 50 % площади импульсов имеют только половинное значение.

Огибающая амплитуд функции 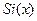есть функция 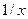Для прямоугольных импульсов с бесконечно большой длительностью периода Т спектральные линии и максимумы функции 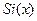бесконечно сближаются. Получается известный спектр 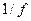ступенчатой функции.

Подобным образом можно рассмотреть и другие формы импульсов с другими огибающими, например, треугольные импульсы, огибающая которых выражается функцией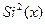

Дата добавления: 2014-01-13