Способы детерминированного факторного анализа

Все явления и процессы хозяйственной деятельности предприятия находятся во взаимосвязи и взаимозависимости. Одни из них непосредственно связаны между собой, другие – косвенно. Каждое явление можно рассматривать и как причину, и как результат.

Каждый результативный показатель зависит от многочисленных и разнообразных факторов. Чем более детально исследуется влияние факторов на величину результативного показателя, тем точнее результаты анализа и оценка качества работы предприятий.

Под факторным анализом понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.

Все способы детерминированного факторного анализа основаны на приеме элиминирования. Элиминирование представляет собой логический прием, при помощи которого исключается влияние ряда факторов и выделяется какой–либо один фактор, являющийся объектом изучения.

Детерминированный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. результативный показатель может быть представлен в виде произведения, частного или алгебраической суммы факторов.

В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.

1. Аддитивные модели:

.

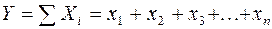Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.

2. Мультипликативные модели:

.

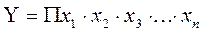Этот тип модели применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.

3. Кратные модели:

.

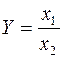Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.

4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей:

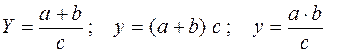и т.д.

Выявление влияния факторов на изменение результативного показателя может быть определено с помощью различных методов.

Индексный метод – метод факторного анализа, когда число факторов равно двум, один из которых количественный, а другой – качественный. Применяется только в мультипликативных моделях.

Алгоритм применения индексного метода:

Y ₀ = a ₀ b ₀ ,

Y ₁ = a ₁ b ₁ ,

где Y ₀, Y ₁ – значение обобщающего показателя, соответственно базовое и фактическое;

а – количественный фактор;

b – качественный фактор.

Индекс роста обобщающего показателя:

.

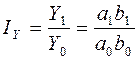При определении влияния количественного фактора " а " качественный фактор берется на базовом уровне:

.

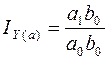При определении влияния качественного фактора " b " количественный фактор фиксируется на фактическом уровне:

.

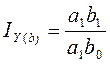Проверка: .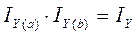

Вычитая из числителя знаменатель, определяют изменение обобщающего показателя Δ Y и влияние факторов на его изменение Δ Y _{( a )} и Δ Y _{( b )} в денежном выражении:

Δ Y = a ₁ b ₁ – а ₀ b ₀;

Δ Y _{( a )} = а ₁ b ₀ – а ₀ b ₀;

Δ Y _{( b )} = а ₁ b ₁ – а ₁ b ₀.

Проверка: Δ Y _{( a )} + Δ Y _{( b )} = Δ Y.

Способ цепных подстановок. Этот способ широко применяется на практике при функциональной прямой или обратной связи между факторами и результативным показателем. Сущность данного способа заключается в том, что, выявляя влияние отдельных факторов на общий результат, последовательно рассматривают каждый из влияющих факторов как переменный при неизменности остальных.

Если результативный показатель является суммой факторов (аддитивная модель - Y = a+b), то его изменение под воздействием каждого фактора находят как разницу между отчетной и базисной величинами составляющего фактора:

D Y _{( a )} = D a;

D Y _{( b )} = D b.

Сумма найденных величин отклонений по факторам должна полностью соответствовать общему изменению результативного показателя:

D Y = Y ₁ – Y ₀ = D Y _{( a )} + D Y _{( b )}.

Если рассматриваемый показатель равен произведению двух факторов (мультипликативная модель), то применяют следующее правило. Факторы обязательно нужно подразделить на объемный (количественный) и качественный.

К количественным относят абсолютные показатели и средние хронологические величины, получаемые на их базе (среднесуточная погрузка в вагонах, работа дороги и т.д.). Важнейшим признаком количественных показателей является возможность суммирования отдельных показателей, рассчитанных внутри совокупности.

Качественные показатели, как правило, характеризуют общее для всех единиц совокупности свойство, они не суммируются (средняя статическая нагрузка на вагон, средняя дальность перевозки, себестоимость перевозок и т.д.).

Для оценки влияния на величину сложного показателя изменений любого фактора необходимо вычислить две условные величины этого показателя – две подстановки. В первой подстановке фактор, влияние которого изучается, берется отчетным. Во второй подстановке этот фактор остается базисным. При этом полагают, что остальные показатели остались неизменными. При определении влияния количественного показателя значение качественного фактора принимается по его базисной величине. Влияние качественных факторов устанавливается только при отчетных количественных показателях.

Размер влияния фактора определяется путем вычитания из последующей подстановки предыдущей (из второй – первой, из третьей – второй и т.д.).

В первую очередь нужно учитывать изменение количественных, а затем качественных показателей.

Рассмотрим расчет влияния факторов на изменение результативного показателя в модели Y = a× b, где Y – результативный анализируемый показатель; а – количественный фактор; b – качественный фактор.

Расчет результативного показателя за базисный период:

Y ₀ = a ₀ × b ₀.

Расчет первой подстановки путем замены базисного значения количественного фактора на его текущее значение:

Y _усл1 = a ₁ × b ₀.

Определение влияния на результативный показатель количественного фактора:

D Y _(a) = Y _усл1 – Y ₀ = a ₁ × b ₀ – a ₀ × b ₀ = (a ₁ – a ₀) × b ₀.

Расчет второй подстановки путем замены базисного значения качественного фактора его текущим значением:

Y _усл2 = a ₁ · b ₁.

Определение влияния на результативный показатель качественного фактора:

D Y _(b) = Y _усл2 – Y _усл1 = a ₁ b ₁ – a ₁ ·b ₀ = (b ₁ – b ₀) ·a ₁.

Сумма найденных величин отклонений по факторам должна полностью соответствовать общему изменению результативного показателя:

D Y = Y ₁ – Y ₀ = D Y _{( a )} + D Y _{( b )}.

В случае, когда рассматриваемый показатель является функцией не двух, а более переменных, то из этой функции нужно выделить ведущий качественный фактор, а оставшаяся часть функции рассматривается как один объемный фактор, имеющий определенное экономическое содержание. Затем применяют сформулированное выше правило для случая с двумя переменными. Далее аналогичным образом рассматривают оставшуюся часть функции и выполняют последующие подстановки, пока не будет выявлено изменение результативного показателя под воздействием всех влияющих факторов.

Рассмотрим расчет влияния факторов на изменение результативного показателя в модели Y = a× (b+с), где Y – результативный анализируемый показатель; а – количественный фактор; b и с – качественные факторы.

Расчет результативного показателя за базисный период:

Y ₀ = a ₀ × (b ₀ + с ₀).

Расчет первой подстановки путем замены базисного значения количественного фактора на его текущее значение:

Y _усл1 = a ₁ × (b ₀ + с ₀).

Определение влияния на результативный показатель количественного фактора:

D Y _{( a )} = Y _усл1 – Y ₀

Расчет второй подстановки путем замены базисного значения качественного фактора b его текущим значением:

Y _усл2 = a ₁ × (b ₁ + с ₀).

Определение влияния на результативный показатель качественного фактора b:

D Y _{( b )} = Y _усл2 – Y _усл1

Расчет третьей подстановки путем замены базисного значения качественного фактора с его текущим значением:

Y _усл3 = a ₁ × (b ₁ + с ₁)= Y ₁.

Определение влияния на результативный показатель качественного фактора с:

D Y _{( c )} = Y _усл3 – Y _усл2

Сумма найденных величин отклонений по факторам должна полностью соответствовать общему изменению результативного показателя:

D Y = Y ₁ – Y ₀ = D Y _{( a )} + D Y _{( b )}+D Y _{( c )}.

Способ абсолютных разниц. Способ абсолютных разниц является одной из модификаций метода цепных подстановок. Как и способ цепных подстановок, применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных моделях и смешанных – типа . Не смотря на его ограниченное использование, этот способ нашел широкое применение в экономическом анализе благодаря своей простоте.

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели, где факторы проранжированы.

Рассмотрим алгоритм расчета для мультипликативной факторной модели типа 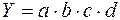. Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения:

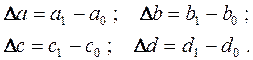
Определим изменение величины результативного показателя за счет каждого фактора:

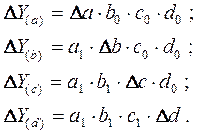
Алгоритм расчета факторов этим способом в смешанных моделях типа будет иметь следующий вид:

.

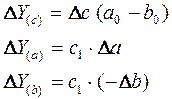Способ относительных величин (коэффициентов). Применяется в тех случаях, когда исходная информация для анализа представлена относительными величинами и не требуется высокой точности расчетов. Необходимым условием применения этого способа является зависимость результативного показателя только от двух факторов:

для мультипликативных моделей –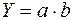

аддитивных моделей –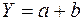

кратных моделей – .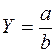

Исходя из теории индексов можно вывести следующие правила:

– темпы прироста показателей для мультипликативных моделей приближенно равны сумме темпов прироста сомножителей, а именно:

,

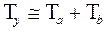где 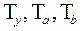– темпы прироста показателей y, a, b, %;

– темпы прироста показателей для аддитивной модели равны сумме темпов прироста слагаемых показателей, взвешенных по соответствующим удельным весам:

,

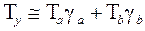где 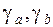– удельный вес или доля величины показателя соответственно а, b в общей величине показателя Y.

В расчетные формулы темпы прироста подставляются всегда в процентах, а удельные веса – в долях;

– темпы прироста показателей для кратной модели приближенно равны разности темпов прироста числителя и знаменателя формулы, а именно:

.

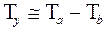Способ пропорционального деления. Этот способ в ряде случаев может быть использован для определения величины влияния факторов на прирост результативного показателя. Это касается тех случаев, когда имеют дело со смешанными моделями, состоящими из факторов первого и второго уровня.

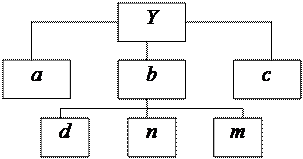
Взаимосвязь факторов в комбинированной модели показана на рис. 2.2.

– Результативный показатель   – Факторы первого уровня   – Факторы второго уровня

Рис. 2.2. Схема взаимодействия факторов

Когда известны 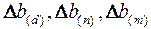, а также 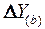, то для определения 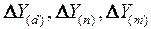можно использовать способ пропорционального деления, который основан на пропорциональном распределении прироста результативного показателя Y за счет изменения фактора b между факторами второго уровня d, n, m соответственно их величине. Пропорциональность этого распределения достигается путем определения постоянного для всех факторов коэффициента, который показывает величину изменения результативного показателя Y за счет изменения фактора b на единицу.

Величина коэффициента К определяется следующим образом:

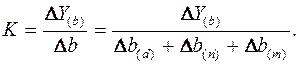
Умножив этот коэффициент на абсолютное отклонение b за счет соответствующего фактора, найдем отклонения результативного показателя:

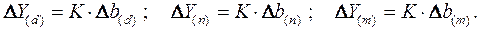
Способ корректировок. Он незначительно отличается от способа подстановок. Отличие – в порядке расчета подстановки.

Для расчета подстановки базисную величину результативного показателя умножают на корректировочный коэффициент 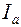. Корректировочный коэффициент представляет собой отношение отчетного значения объемного фактора к базовому:

;

,

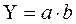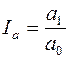где 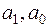– объемные показатели соответственно за текущий и базисный периоды.

Влияние факторов на результативный показатель определяется следующим образом:

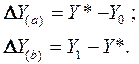
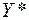– условная подстановка – определяется:

.

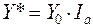Проверка правильности расчетов:

,

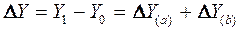где – соответственно изменение результативного показателя под влиянием факторов соответственно объемного а, качественного b и общее изменение;

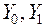– базисное и текущее значения результативного показателя.

Способ структурных сдвигов. Применяется при анализе качественных показателей, зависящих от состава (структуры) изучаемых явлений. Величина качественных показателей выражается формулой взаимосвязи как сумма произведений структурных коэффициентов 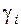на частные качественные факторы :

.

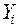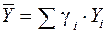Например, средняя статическая нагрузка зависит от породовой структуры грузов и статических нагрузок каждого рода грузов; средняя дальность перевозки 1 т груза зависит от структуры перевозимых грузов, дальности перевозки каждого рода груза и т.п.

Для анализа изменений результативного качественного показателя рассчитывают его условную величину – подстановку, в которой структурные коэффициенты принимаются на отчетном, а частные качественные факторы – на базисном уровнях.

,

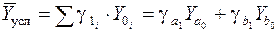где 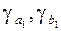– фактическая структура изучаемого явления;

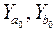– базовое значение частных факторов.

Влияние на результативный показатель структурных сдвигов оценивают при сравнении подстановки с базисной величиной результативного показателя, а влияние частных качественных факторов – при сравнении отчетной величины результативного показателя и подстановки.

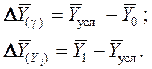
При расчетах по вышеприведенным формулам получена оценка одновременного изменения всех частных качественных факторов. Чтобы выделить влияние каждого из этих факторов, их изменения умножают на отчетный уровень соответствующего структурного коэффициента:

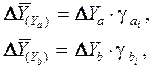
причем

.

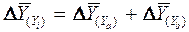Для оценки структурных изменений необходимо изменение данного структурного коэффициента умножить на разность между базисными величинами соответствующего частного качественного фактора и результативного качественного показателя:

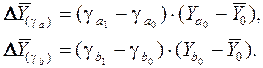
Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом деле они изменяются совместно, взаимосвязано, и от этого взаимодействия получается дополнительный прирост результативного показателя (неразложимый остаток), который при применении элиминирования присоединяется к одному из факторов, как правило, к показателю, анализируемому в последнюю очередь. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели.

В последнее время применяются и другие способы факторного анализа, упрощающие расчеты и дающие более точное распределение приращения результативного показателя между факторами: интегральный, метод взвешенных конечных разностей, логарифмический, кольцевой и экстремальный.

Дата добавления: 2014-01-13