Применение законов Кирхгофа

Классификация воздействий в электрических цепях

Воздействия в электрических цепях

Воздействиями в электротехнике называют различные проявления электромагнитных сил, приводящие к изменению состояния электрической цепи. Под влиянием воздействий в электрической цепи возникают реакции, которые определяются как видом воздействия, так и характеристиками самой цепи. При этом основными величинами, характеризующими состояние электрической цепи, являются электрические напряжение и ток.

Все воздействия в электрических цепях можно разделить по их назначению на регулярные, или детерминированные и нерегулярные, или случайные.

Детерминированными называют воздействия, заданные в виде некоторой определённой функции времени. Такие воздействия обычно используются для передачи энергии или при измерениях. Детерминированные воздействия можно разделить на периодические и непериодические.

Периодическими называют воздействия, для которых существует отрезок времени Т, отвечающий условию периодичности х(t) = x(t + nT), где n = ± 1, ± 2…

К периодическим воздействиям относятся гармонические колебания и периодические последовательности импульсов различной формы.

Если воздействия не отвечают условию гармоничности, то они называются непериодическими.

К непериодическим воздействиям относят одиночные импульсы или группы импульсов различной формы.

Случайными называют воздействия, являющиеся произвольными функциями времени. К случайным воздействиям относятся различные виды помех от действия источников внутренних шумов в электронных приборах, резисторах и других элементах электрических цепей.

Гармонические воздействия являются основным видом возмущений и реакций в энергетических сетях и системах.

Генерирование гармонических напряжений и токов в диапазоне частот 10 – 10³ Гц обычно производится электромеханическими генераторами, а более высоких частот – с помощью электронных устройств.

К гармоническим воздействиям относят синусоидальные и косинусоидальные функции, аргументом которых является время или угол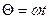

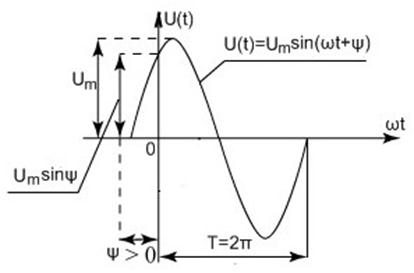Значение напряжения, тока, ЭДС в любой момент времени называют мгновенным.

T = 2π – период

f = 1/T – частота ЭДС, напряжения, тока (Гц)

U_m – амплитуда (максимальное значение)

ω= 2πf – скорость изменения аргумента, называемая угловой частотой (рад/сек, 1 рад = 57,3^о)

Ψ – начальная фаза, определяемая величиной смещения гармонической функции относительно начала координат.

За аргумент функций может быть принято время (t) или угол (ωt). ωt + Ψ – называется начальной фазой (углом).

Ток определён, если известна его зависимость от времени i = f(t) и указано положительное направление тока.

За один период переменного тока в проводнике с сопротивлением R выделяется тепловая энергия

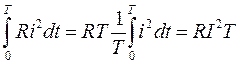
Отсюда следует, что действующий ток численно равен такому постоянному току, при котором за один период в проводнике с тем же сопротивлением выделяется такое же количество тепла, что и при переменном.

3.2. Закон Ома (в обобщённой форме)

Закон Ома применяется для расчёта токов и напряжений в отдельных ветвях цепи или для одноконтурной замкнутой цепи, не имеющей разветвлений.

При написании закона Ома следует прежде всего выбрать произвольно некоторое положительное направление тока.

Для ветви, состоящей только из сопротивлений и не содержащей ЭДС (см. рис.3.1. для ветви «ba»), при положительном направлении тока от (·) b к (·) a имеем:

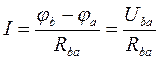, где

φ_b, φ_a – потенциалы точек (узлов a,b);

U_ba – разность потенциалов между точками b и a;

R_ba - эквивалентное сопротивление цепи, R_ba=R₁+R₂

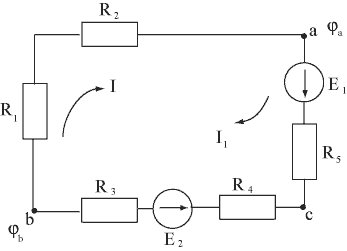
Рис.3.1

Для ветви, состоящей из сопротивлений и ЭДС (ветвь acb), рис.3.1 ток равен:

, где

U_ab – напряжение на концах ветви acb, отсчитываемое по выбранному положительному направлению тока;

ΣE – алгебраическая сумма ЭДС, находящаяся в этой ветви (Е1+Е2)

1. Устанавливаются условно положительные направления токов в ветвях электрической цепи.

2. Выбираются независимые контуры ( контур, содержащий хотя бы один новый элемент).

3. Определяется число уравнений по I закону Кирхгофа. Их число равно:

где N_y – число узлов электрической цепи;

N_н – число источников напряжений, если они расположены между узлами, не имеющими сопротивлений.

4. Составляются уравнения по I закону Кирхгофа;

5. Определяется число уравнений по II закону Кирхгофа:

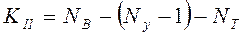
где N_B – число ветвей, N_y – число узлов;

N_T – число источников тока, если они расположены между узлами, не имеющими проводимостей.

6. Составляются уравнения по II закону Кирхгофа.

При составлении уравнений по II закону Кирхгофа следует выбирать независимые контуры, т.е. не содержащие источников тока.

Выбирается произвольное направление обхода контуров (произвольно).

При записи левой части равенства ЭДС, направления которых совпадают с выбранными направлениями обхода контура (независимо от направления тока, протекающего через них), принимаются положительными, а ЭДС, направленные против выбранного обхода, - отрицательными.

При записи правой части равенства со знаком «плюс» берутся падения напряжения в тех ветвях, в которых выбранное положительное направление тока совпадает с направлением обхода (независимо от направления ЭДС в этих ветвях), и со знаком «минус», падения напряжения в тех ветвях, в которых положительное направление тока противоположно направлению обхода контура.

3.4. Пример расчёта цепи постоянного тока с применением законов Кирхгофа.

Решение:

К_I = N_y – 1 – N_н = 4 – 1 – 0 = 3

Выбираем (·)a, (·)b, (·)c.

(·)a: I₃ – I₁ = 0

(·)b: I₄ – I₂ – I₃ = 0

(·)c: I₆ + I₁ – I₄ = 0

K_II = N_B – (N_y – 1) – N_T = 6 – (4 – 1) – 0 = 3

R₃ I₃ + R₁ I₁ + R₄ I₄ = E₁ (I)

R₁ I₁ – R₅ I₅ – R₆ I₆ = E₁ (II)

R₂ I₂ + R₆ I₆ + R₄ I₄ (III)

К = КI +KII – общее число уравнений системы для определения токов I1÷I6. Решаем систему любым методом.

Вторым законом Кирхгофа можно пользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в левую часть уравнений исходное напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения U_mn можно написать уравнение для контура mncb или nmbc:

Раздел 4.

Дата добавления: 2014-01-13