Соединение генератора и нагрузки треугольником

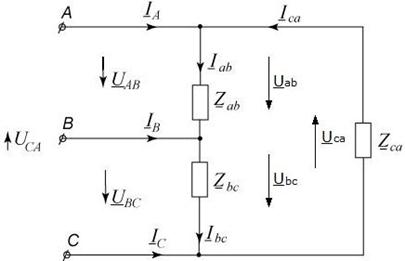
Соединение, выполненное треугольником, представляет собой такое включение фаз генератора или приёмника, при котором начало одной фазы соединяется с концом другой и т.д.

При соединении треугольником фазные напряжения равны линейным, а линейные токи равны геометрической разности двух фазных токов, подходящих к вершине треугольника.

Поэтому для положительных направлений сил тока, указанных на рис.8.11. справедливо:

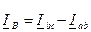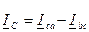; ; (8.15)

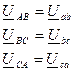(8.16)

рис.8.11.

*При расчёте трехфазных электрических цепей принято использовать комплексную форму записи уравнений.

Фазные токи рассматриваются по известным линейным напряжениям и проводимостям фаз приёмника:

; ; (8.17)

8.10. Рассмотрим различные режимы работы трехфазной системы при соединении генератора и приёмника треугольником.

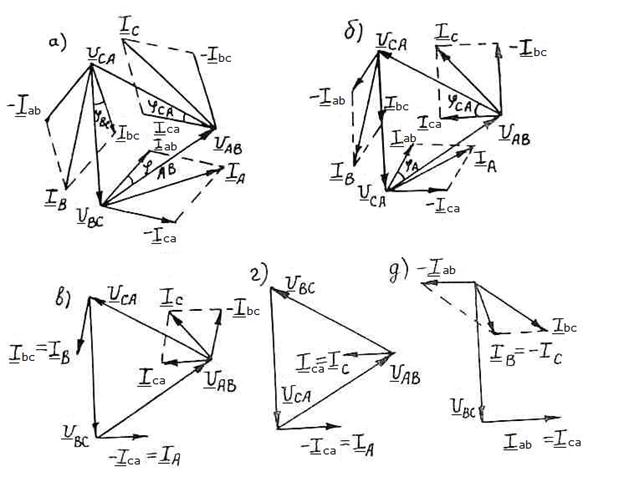
рис.8.12

Равномерная нагрузка фаз генератора

При симметричной системе ЭДС генератора и равномерной нагрузке фаз () действующие значения сил тока в фазах равны между собой, поэтому линейные токи в фазах равны между собой с фазными токами соотношением .

Векторная диаграмма напряжений и сил тока для этого случая на рис.8.12,а.

б) Неравномерная нагрузка фаз генератора

При симметричной системе ЭДС генератора и неравномерной нагрузке фаз () действующие значения сил тока в фазах пропорциональны их проводимостям в соответствии с выражением (8.17).

Векторная диаграмма напряжений и тока для этого случая приведена на рис.8.12,б.

Обрыв одной фазы приёмника

При обрыве одной фазы приёмника сила тока в ней будет равна нулю. Силы тока двух других фаз не изменятся, также как и фазные напряжения. В линейном проводе, не связанном с оборванной фазой, сила тока не изменится. Линейные токи двух фаз станут равными фазным. В случае обрыва фазы () получим:

; ;

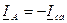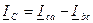
Векторная диаграмма напряжений и тока для этого случая приведена на рис.8.12,в.

Обрыв двух фаз приёмника

При обрыве двух фаз приёмника сила тока в них будет равна нулю. Сила тока в неповреждённой фазе не изменится. Сила тока в линейном проводе, подходящем к оборванным фазам, будет равна нулю, а величины тока в других линейных проводах будут равны фазным. Так, например, при обрыве фаз и 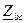() получим:

; ;

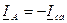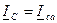
Векторная диаграмма напряжений и сил токов в этом случае приведена на рис.8.12,г.

Обрыв линейного провода

При обрыве одного линейного провода трехфазная система превращается в однофазную. Напряжение и сила тока в фазе, связанной с оборванным линейным проводом, равны нулю. Две другие фазы оказываются соединёнными последовательно и подключенными параллельно к первой фазе. Так, например, при обрыве линейного провода А фазы и 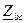, включённые последовательно, оказываются подключенными параллельно к фазе ВС, напряжение которой равно .

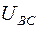Векторная диаграмма напряжений и токов для этого случая показана на рис.8.12,д.

Выводы

1. Постоянство мгновенных значений мощности создаёт благоприятные условия для работы генераторов и двигателей с точки зрения их механической нагрузки, так как отсутствуют пульсации вращающего момента.

2. Передача энергии на дальние расстояния трехфазным током экономически более выгодна, чем переменным током с иным числом.

3. Элементы системы – трехфазный АД и трехфазный трансформатор – весьма просты в производстве, экономичны и надёжны в работе.

8.11 Мощность в трёхфазных цепях

Мгновенная мощность трёхфазного генератора равна сумме мгновенных мощностей всех трёх фаз:

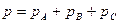(8.18)

или

(8.19)

При отсутствии нейтрального (нулевого) провода уравнение (8.18) приобретает вид:

,

так как в этом случае , а по определению

Активная мощность Р трёхфазного генератора согласно (8.18), равна сумме активных мощностей всех трёх фаз

,

которая в соответствии с () приводится к виду

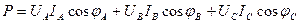
В симметричной системе

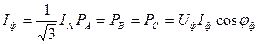(8.20)

и, следовательно, независимо от схемы соединения фаз

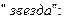
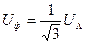
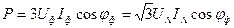(8.21)

Применяя (8.18) к расчёту мгновенного значения мощности в трёхфазной симметричной системе, можно убедиться, что р = Р, т.е. сумма мгновенных значений мощностей всех трёх фаз – величина постоянная.

где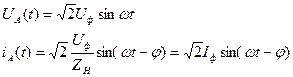

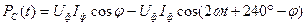
р = Р à Постоянство мощности в симметричном решении – одно из крупных достоинств трёхфазной (и вообще – многофазной) цепи. При этом трёхфазные электродвигатели и генераторы имеют благоприятные условия для работы, так как в таком решении отсутствуют пульсации момента, что наблюдается у однофазных электрических машинах.

Реактивная мощность Q трёхфазного генератора определяется как алгебраическая сумма реактивных мощностей всех фаз:

(8.22)

и, в частности, для симметричной системы независимо от схемы соединения фаз

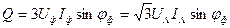(8.23)

Полная мощность S симметричной трёхфазной системы определяется согласно ()

(8.24)

Коэффициент мощности λ для трёхфазной цепи вычисляется как

(8.25)

Запишем комплексную форму полной мощности 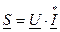, где - комплексная полная мощность, 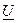- комплексное действующее значение напряжения, - сопряжённое комплексное действующее значение тока.

(8.26)

Р – активная мощность, Q – реактивная мощность

Для трёхфазной цепи:

(8.27)

Действительная часть этого выражения представляет собой активную мощность:

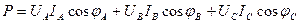(8.28)

Суммарная активная мощность, потребляемая несимметричной трёхфазной цепью, может быть в соответствии с этим выражением измерена при помощи трёх ваттметров, активная мощность равна сумме показаний трёх ваттметров. Такой метод измерения применяется при наличии нейтрального провода, или искусственно создаётся нейтральный ток.

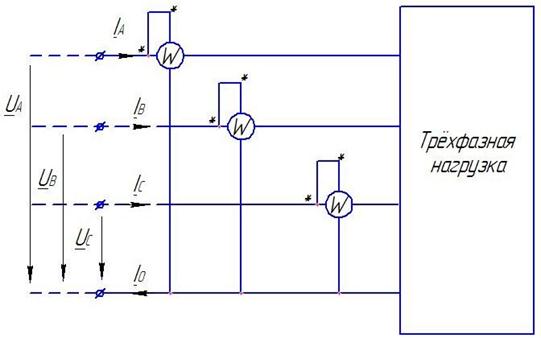
Рис.8.13.

В случае отсутствия нейтрального (нулевого) провода измерение может быть произведено с помощью двух ваттметров (рис.8.14).

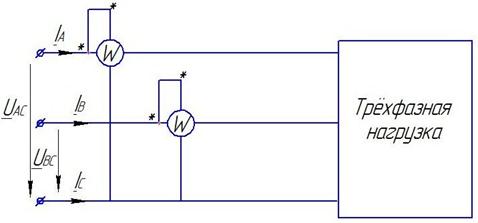
Рис.8.14.

В этом случае выражение (8.27) преобразуется следующим образом: искомый ток из условия:

, получаем:

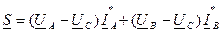или

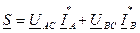(8.29)

В соответствии с (8.29) при изменении активной мощности двумя ваттметрами к одному из них подводится напряжение и ток 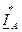, к другому – напряжение 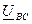и ток (рис.8.14.). Показания ваттметров складываются алгебраически.

Информационно-методическое обеспечение дисциплины:

1. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Т1, Т2. - М.: Высшая школа, 1981.
2. Бессонов Л.А. Теоретические основы электротехники. Т1, Т2. - М.: Высшая школа, 1984.
3. Ионкин П.А. и др. Теоретические основы электротехники. Т1. - М.: Высшая школа 1981.
4. Основы теории цепей /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов/ М.: Высшая школа, 1989.
5. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. – М.: Высшая школа, 1990.
6. Матханов П.Н. Основы анализа электрических цепей. Нелинейные цепи. – М.: Высшая школа, 1990.
7. Сборник задач и упражнений по ТОЭ под ред. П.А. Ионкина. – М.: Энергоиздат, 1982.
8. Шебес М.Р. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1989.
9. Задачник по ТОЭ под ред. К.М. Поливанова– М.: Энергия, 1975.
10. Дмитриев Б.Ф. Общая электротехника. Линейные электрические цепи.

Дата добавления: 2014-01-13