Числовая последовательность. Предел числовой последовательности

Периодичность.

Опр. 5. Функция у=f(x) называется периодической, если существует положительное число Т такое, что f(х+Т)=f(x). Наименьшее число с таким свойством называется периодом функции.

Для построения графика периодической функции достаточно изобразить его на отрезке, длина которого равна периоду (основная область), а затем построить периодическое продолжение графика, повторяя график, нарисованный в основной области.

Опр. 1. Последовательностью называется числовая функция f(n), заданная на множестве натуральных чисел N.

Если n — натуральное число, а а_n - значение последовательности в точке n, то говорят, что n называется номером числа а _n, а само число а_n называют общим или n-м членом последовательности. Для последовательности с общим членом а _n употребляются следующие обозначения: а _n, n=1, 2, …, или { a _n}.

Опр. 2. Последовательность { a _n} называется постоянной, если a _n= с для любого , где с – некоторое действительное число ().

Опр. 3. Последовательность { a _n} называется ограниченной, если найдется число М такое, что | а_n |≤ М для всех .

Опр. 4. Последовательность { a _n} называется возрастающей (убывающей), если a _n≤ a _n+1 (a _n≥ a _n+1) для любого . Возрастающие и убывающие последовательности называются монотонными последовательностями.

Опр. 5. Последовательность { a _n} называется строго возрастающей (строго убывающей), если a _n< a _n+1 (a _n> a _n+1) для любого . Строго возрастающие и строго убывающие последовательности называются строго монотонными последовательностями.

Опр. 6. Число а называется пределом числовой последовательности { а_n }, если для любого, даже сколь угодно малого положительного числа 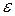>0, найдется такое число N (зависящее от 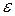, N=N (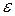)), что для всех членов последовательности с номерами n>N верно неравенство | а_n – а| <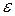. Если это выполняется, то пишут

Теорема 1. Если последовательность ограничена и монотонна, то она сходится.

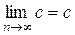Теорема 2. Пусть дана постоянная числовая последовательность { a _n}, где a _n = с = const для любого . Тогда она сходится и (предел постоянной равен постоянной).

Теорема 3. Последовательность { a _n} с общим членом a _n=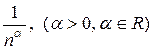сходится и

Теорема 4. Если | q | < 1 (), то последовательность { q _n} сходится и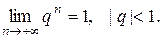

Теорема 5. Предел суммы равен сумме пределов.

Теорема 6. Предел произведения равен произведению пределов.

Теорема 7. Постоянную величину можно выносить за знак предела.

Теорема 8. Предел отношения равен отношению пределов (знаменатели справа и слева от знака равенства не равны нулю).

Дата добавления: 2014-01-13