КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П. 1. Интегрирование некоторых тригонометрических функций
|
|
|
|
Интегрирование некоторых иррациональных и тригонометрических функций
П. 3. Интегрирование рациональных функций
Пусть нам дана рациональная функция. Если она представляет собой правильную дробь, то интегрировать ее мы уже умеем. Если дробь неправильная, то выделив из нее целую часть (разделив числитель на знаменатель), сведем вычисление интеграла к вычислению правильной дроби.
При вычислении интегралов вида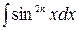 
или 
при n четном нужно представить его в виде 
раскрыть скобки и, если потребуется, повторно применить формулу 
При вычислении интегралов вида 
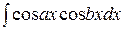применяются формулы:
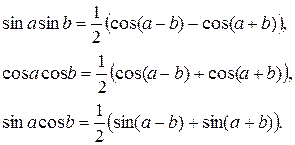
При вычислении интегралов вида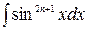 
и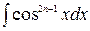 
(n – целое положительное число) для первого интеграла за вспомогательную функцию нужно принять 
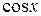и для второго 
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 258; Нарушение авторских прав?; Мы поможем в написании вашей работы!