Двойной интеграл

Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией L. Разобьем эту область какими-нибудь линиями на n частей ∆S₁, ∆S₂,…, ∆S_n (причем теми же символами ∆S₁, ∆S₂,…, ∆S_n будем обозначать и площади соответствующих частей) и выберем в каждой части точку Р_i.

Пусть в области D задана функция z=f(x,y). Обозначим через f(P₁), f(P₂),…, f(P_n) значения этой функции в выбранных точках и составим сумму произведений вида f(P_i)ΔS_i: 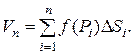(1)

Опр. 1. Сумма вида 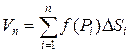называется интегральной суммой для функции f(x,y) в области D.

Замечание. 1. С геометрической точки зрения (при 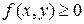) интегральная сумма (1) представляет собой сумму объемов цилиндров с основаниями ΔS_i и высотами f(P_i).

Опр. 2. Если существует один и тот же предел интегральных сумм (1) при n→∞ и max∆S_i →∞, не зависящий от способа разбиения области D и выбора точек P_i, то он называется двойным интегралом от функции f(x,y) по области D и обозначается Область D при этом называется областью интегрирования.

Замечание 2. Для выяснения вопроса об условиях интегрируемости функции двух переменных можно по аналогии со случаем определенного интеграла ввести понятие верхней и нижней интегральных сумм, выбирая в каждой части области D точки, значение функции в которых является наибольшим и наименьшим для данной части. Тогда можно доказать, что необходимым и достаточным условием интегрируемости функции f(x,y) является, во-первых, ее ограниченность на D, а во-вторых, условие 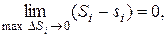где i – некоторое разбиение, а S_i и s_i – соответственно верхняя и нижняя интегральные суммы.

Замечание 3. Если функция f(x,y) непрерывна на D, то она интегрируема по этой области.

Свойства двойных интегралов:

Часть свойств двойных интегралов непосредственно вытекает из определения этого понятия и свойств интегральных сумм, а именно:

1. Если функция f(x,y) интегрируема в D, то kf(x,y) тоже интегрируема в этой области, причем

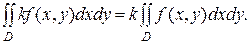
2. Если в области D интегрируемы функции f(x,y) и g(x,y), то в этой области интегрируемы и функции f(x,y)±g(x,y), и при этом

3. Если для интегрируемых в области D функций f(x,y) и g(x,y) выполняется неравенство f(x,y)≤g(x,y), то

4. Если область D разбита на две области D₁ и D₂ без общих внутренних точек и функция f(x,y) непрерывна в области D, то

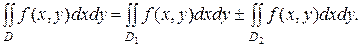
5. В случае интегрируемости на D функции f(x,y) в этой области интегрируема и функция | f(x,y) |, и имеет место неравенство

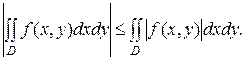
6. 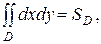где S_D – площадь области D.

7. Если интегрируемая в области D функция f(x,y) удовлетворяет неравенству m≤f(x,y)≤M, то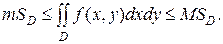

Следствие ( теорема о среднем).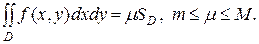

В частности, при условии непрерывности функции f в D найдется такая точка этой области (х₀,у₀), в которой f(х₀,у₀)=μ, то есть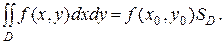

Дата добавления: 2014-01-13