Функции комплексного переменного

Определение функции комплексной переменной ничем не отличается от общего определения функциональной зависимости. Напомним, что областью на плоскости мы называем любое открытое связное множество точек этой плоскости. Область односвязна, если любая подобласть, ограниченная непрерывной замкнутой самонепересекающейся кривой, лежащей в этой области, целиком принадлежит области.
Рассмотрим две плоскости комплексных чисел: C = { z | z = x + iy } и W = { w | w = u + iv }. Пусть в плоскости С задана область D и задано правило, ставящее в соответствие каждой точке z ∈ D определённое комплексное число w ∈ W. В этом случае говорят, что на области D определена однозначная функция w = f (z) (или определено отображение f: z → w). Область D называется областью определения функции, множество { w | w ∈ W, w = f (z), z ∈ D } - множеством значений функции (или образом области D при отображении f.
Если каждому z ∈ D ставится в соответствие несколько значений w ∈ W (т.е. точка z имеет несколько образов), то функция w = f (z) называется многозначной.
Функция w = f (z) называется oднолистной в области D ⊂ C, если она взаимно однозначно отображает область D на область G ⊂ W (т.е. каждая точка z ∈ D имеет единственный образ w ∈ G, и обратно, каждая точка w ∈ G имеет единственный прообраз z ∈ D.
Действительная и мнимая часть функции комплексной переменной.

Так как w = u + iv, z = x + iy, то зависимость w = f (z) можно записать в виде w = u + iv = f (z) = f (x + iy) = Re f (x + iy) + i Im f (x + iy). Таким образом, задание комплекснозначной функции w = f (z) комплексной переменной z равносильно заданию двух действительных функций u = u (x, y) = Re f (z), v = v (x, y) = Im f (z) двух действительных переменных х, у.
Примеры: 1. w = z ³. Выражаем z ³ через х, у: z ³ = (x + iy)³ = x ³ + 3 x ² i y + 3 xi ² y ² + i ³ y ³ =

2. w = e ^z. Здесь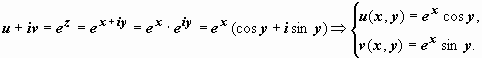
Дальше многие свойства ФКП (функций комплексной переменной) мы будем формулировать в терминах её действительной части u (x, y) и мнимой части v (x, y), поэтому техника выделения этих частей должна быть хорошо отработана.
Геометрическое изображение ФКП.

Задание функции w = f (z) как пары u = u (x, y), v = v (x, y) наводит на мысль изображать ФКП как пару поверхностей u (x, y), v (x, y) в трёхмерном пространстве, однако этот способ неудобен, так как он не позволяет осмыслить пару (u, v) как комплексное число. Иногда изображают поверхность 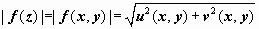, которую называют рельефом функции w = f (z). На эту поверхность наносят линии уровня функции Arg f (z); при наличии определенного опыта этой информации достаточно для того, чтобы составить представление об изменении функции в полярных координатах. Однако универсальный способ изображения ФКП состоит в том, что рисуют множества, соответствующие друг другу при рассматриваемом отображении. Чаще всего берут координатные линии (декартовых или полярных координат) и находят их образы.
Примеры. 1. Линейная функция w = a z + b, где a = a ₁ + ia ₂ = | a |· e^{i arg a}, b = b ₁ + ib ₂ - фиксированные комплексные числа, a ₁, b ₁ - их действительные части, a ₂, b ₂ - их мнимые части.
Представим эту функцию в виде суперпозиции двух функций: w ₁ = az и w = w ₁ + b. Отображение z → w ₁ = az, согласно интерпретации умножения чисел в тригонометрической форме, приводит к увеличению (уменьшению) аргумента числа z наarg a и растяжению (сжатию) его модуля в | a | раз; отображение w ₁ → w = w ₁ + b приводит к сдвигу точки: w ₁ на вектор: b (b ₁, b ₂). Таким образом, линейная функция w = a z + b растягивает (при | a | ≥ 1) каждый вектор z в | a | раз (или сжимает его в раз при | a | <1), поворачивает на угол arg a и сдвигает на вектор b. В результате все прямые преобразуются в прямые, окружности - в окружности.
2. Степенная функция w = z ². Рассмотрим эту функцию в верхней полуплоскости C ⁺ = { z | y = Im z >0}. В показательной форме w = z ² = (| z |· e ^i· arg z)² = | z | ²· e ^{2 i arg z}. Следовательно, полуокружность{| z | = r, 0 < arg z < π} переходит в окружность с выколотой точкой {| w | = r ², 0 < arg z < 2π}, луч{0 < | z | < ∞, arg z = φ₀} - в луч {0 < | w | < ∞, arg z = 2φ₀}. Вся верхняя полуплоскость С ⁺ перейдёт в плоскость W с выброшенной положительной полуосью.
Представим это отображение в декартовых координатах. Так как w = z ² = (x + iy)² = x ² - y ² + 2 ixy, то u (x, y) = x ² - y ², v (x, y) = 2 xy. Найдём образы координатных линий. Прямая y = y ₀ перейдёт в кривую, параметрические уравнения которой u = x ² – y ₀², v = 2 xy ₀ (х - параметр). Исключая х, получим уравнение параболы . Луч { x = x ₀, 0 < y < ∞} перейдёт в u = x ₀² – y ², v = 2 x ₀ y (параметр y >0). Исключая у, получим ветвь параболы . Из v = 2 x ₀ y следует, что v сохраняет знак x ₀, поэтому это будет верхняя ветвь при x ₀ >0, и нижняя при x ₀ <0. Луч x ₀ = 0 перейдет в луч u < 0, v = 0.
Мы рассматриваем функцию w = z ² в верхней полуплоскости С ⁺, несмотря на то, что она определена во всей плоскости С, по той причине, что она однолистна в этой полуплоскости. Нижняя полуплоскость C ^- = { z | y = Im z <0} при отображении w = z ² также накроет всю плоскость W (за исключением положительной полуоси). Если рассматривать весь образ плоскости С при этом отображении, то он будет состоять из двух экземпляров плоскости W (двух листов, накрывающих эту плоскость).
На этом примере мы получили алгоритм построения образов линий и областей при отображении w = f (z). Если w = u (x, y) + iv (x, y), то, чтобы найти уравнение образа линии L: F (x, y) = 0 при отображении, надо из системы уравнений исключить переменные х и у; в результате будет получено уравнение Φ (u, v) = 0 образа линии L в плоскости W. Чтобы найти образ области D, ограниченной замкнутой кривой L, надо найти образ этой линии, если образ - замкнутая линия, дальше надо определить, переходит ли D в область, ограниченную этой линией, или во внешность этой области.
Пример: пусть z ₁ = 1 + i, z ₂ = 2 + i, z ₃ = 1 + 2 i. Найти образ треугольника z ₁ z ₂ z ₃ при отображении w = z ².
Находим, куда отображаются вершины треугольника. w ₁ = z ₁² = (1 + i)² = 1 + 2 i - 1 = 2 i; w ₂ = z ₂² = (2 + i)² = 4 + 4 i - 1 = 3 + 4 i; w ₃ = z ₃² = (1 + 2 i)² = 1 + 4 i - 4 = -3 + 4 i. Сторона z ₁ z ₂ является частью прямой у = у ₀=1. Эта прямая отображается, как мы видели, в параболу 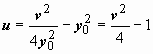. Нам нужна часть этой параболы между точками w ₁ и w ₂. Далее, сторона z ₁ z ₃ является частью прямой х = х ₀=1, отображаемой в параболу ; берём участок этой параболы между точками w ₁ и w ₃. Сторона z ₂ z ₃ лежит на прямой х + у =3; уравнение образа этой прямой получим, исключив из системы 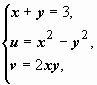переменные х и у: . Участок этой параболы между точками w ₂ и w ₃ и даст образ стороны z ₂ z ₃. Изображение треугольника построено. Легко убедиться, что область, ограниченная этим треугольником, переходит во внутренность криволинейного треугольника w ₁ w ₂ w ₃ (для этого достаточно найти, например, образ одной точки этой области).
3. Более общая степенная функция w = z ⁿ, где n - натуральное число, действует аналогично функции w = z ². Так как w = zⁿ = (| z | e ⁱ arg z) ⁿ = | z | ⁿe ^{i n} arg z, то это отображение увеличивает в n раз все углы с вершиной в точке z = 0. Любые две точки z ₁ и z ₂ с одинаковыми модулями и аргументами, отличающимися на число, кратное 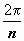(и только они), переходят в одну точку w, т.е. "склеиваются" при отображении. Следовательно, отображение неоднолистно ни в какой области, содержащей такие точки. Пример области, в которой это отображение однолистно - сектор . Этот сектор преобразуется в область G = { w | 0 < arg w < 2π}, т.е. в плоскость W с выброшенной положительной полуосью. Любая область, заключенная в секторе раствора меньше 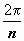, однолистно отображается в W.

Предел ФКП
Определение. Пусть функция w = f (z) определена в проколотой окрестности точки z ₀ = x ₀ + iy ₀. Комплексное число w ₀ = u ₀ + iv ₀ называется пределом функции при z → z ₀, если для любой ε-окрестности U (w ₀, ε) (ε>0) точки w ₀ найдётся такая проколотая δ-окрестность 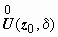точки z ₀, что для всех 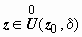значения f (z) принадлежат U (w ₀, ε). Другими словами, если z ₀ - собственная точка плоскости, то для любого ε > 0 должно существовать такое δ > 0, что из неравенства 0 < | z − z ₀| < δ следует неравенство | f (z) − w ₀| < ε (аналогично расписывается определение для несобственной точки z ₀ = ∞). Таким образом, на языке ε - δ определение предела ФКП полностью совпадает с определением предела функции одной действительной переменной; обозначается предел, как обычно: .
Неравенство | f (z) − w ₀| < ε означает, что |(u (x, y) + iv (x, y)) − (u ₀ + iv ₀)| < ε, или |(u (x, y) - u ₀) + i (v (x, y) − v ₀)| < ε. Для модуля комплексных чисел справедливы все основные свойства абсолютной величины, в частности | z ₁ + z ₂| ≤ | z ₁| + | z ₂|, поэтому |(u (x, y) - u ₀) + i (v (x, y) − v ₀)| < ε Отсюда легко получить, что 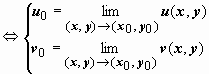. Таким образом, существование предела функции комплексной переменной равносильно существованию пределов двух действительных функций u (x, y) и v (x, y) двух действительных переменных. Поэтому в комплексный анализ автоматически переносятся все теоремы о пределах функции в точке (предел суммы функций и т.д.). Так же можно доказать, что если w ₀ = | w ₀|·(cos arg w ₀ + i sin arg w ₀) ≠ 0, то (для существования нулевого предела достаточно, чтобы ).

Дата добавления: 2014-01-13